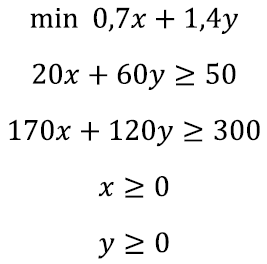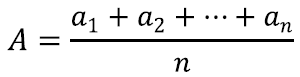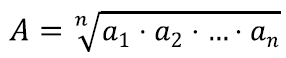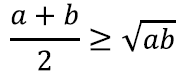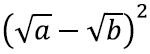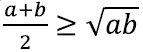Võrratus

Nagu nägime, võimaldab võrrand [lk 168] üsna täpselt ja arvuliselt tingimusi ja seoseid kirja panna. Mõnikord ei ole aga tingimused nii põhjalikud, et neid saaks võrrandiga kirja panna, ning mõnikord ei huvitagi meid see, millised on suuruste täpsed väärtused. Meid huvitab ainult nende suuruste vaheline seos – mis on suurem, mis väiksem.Näiteks valides kahe rahapauna vahel, ei huvita rahalembelist, kui palju on täpselt ühes või teises paunas raha, vaid huvitab pigem, kummas paunas on rohkem raha. Samuti ei huvita meid näiteks kahe marsruudi vahel valides, kui pikad teekonnad täpselt on, vaid kumb on lühem, kumb pikem.Ka võrrandi peatükis toodud näited oleksid loomulikumad võrratuste keeles. Küsime ju tegelikult, mitu inimest maksimaalselt mahuks nii või nii suurele laululavale. Nii saaksime ka toodud võrrandi asemele hoopis võrratuse.

Märk ≤ asetataksegi kahe suuruse vahele, kui vasem on paremast väiksem või sellega võrdne. Märk < isepäini tähendab, et vasem suurus on paremast rangelt väiksem ehk võrdus pole sel juhul lubatud. Näiteks π < 3,5 tähendab, et arv π on arvust 3,5 väiksem. Mõlemat märki võib muidugi kasutada ka teisipidi, näiteks 3,5 > π.

Võrratuste koostamine

Nagu võrrandi korralgi, koostame ka võrratusi tihti mõne elulise situatsiooni kirjeldamiseks või mõne elulise küsimuse lahendamiseks. Võrratuste ja võrrandite koostamine on väga sarnane – seame elulistele suurustele vastavusse muutujad ja määrame nendevahelised suhted.

Meenutame näiteks mobiilioperaatorite näidet. Meil oli kaks operaatorit järgmiste pakettidega:

operaator A: 5 eurot kuumakse pluss 0,01 eurot kõneminut,
operaator B: 1 eurot kuumakse pluss 0,02 eurot kõneminut

Võrrandi peatükis küsisime, kui palju peaksime telefoniga rääkima, et operaatorite juures oleksid kuutasud võrdsed. Kuna on aga selge, et operaator A muutub soodsamaks, kui räägime palju, oleks loomulikum küsida: kui palju peaksime telefoniga rääkima, et operaator A muutuks soodsamaks?

Kuna kuutasu sõltub mõlemal juhul otseselt räägitud kõneminutite arvust, tuleb ta kindlasti mängu tuua ning võime ta tähistada näiteks muutujaga k. Seega võime kuutasud välja kirjutada järgmiselt:

Operaator A juures: 5 + 0,01k eurot
Operaator B juures: 1 + 0,02k eurot

Meie küsimust, millal on operaator A kuutasu odavam, esitab siis täpselt võrratus:

Nagu võrranditegi korral, on võrratuses endas nüüd kontekst kadunud: küsime lihtsalt, milliste k-de korral on vasem pool väiksem paremast. Pärast võime vastuse tõlkida jälle elukeelde ja vastatagi, milliste kuuminutite arvu korral on operaator A pakett odavam.

Nüüd räägimegi võrratuste lahendamisest lähemalt.

Sulle võivad huvi pakkuda need õppematerjalid:

Võrratuste lahendamine

Võrratuse lahendamine tähendab täpselt sama, mida võrrandi lahendaminegi – tuleb leida antud tingimustega sobivad muutuja väärtused [lk 176].

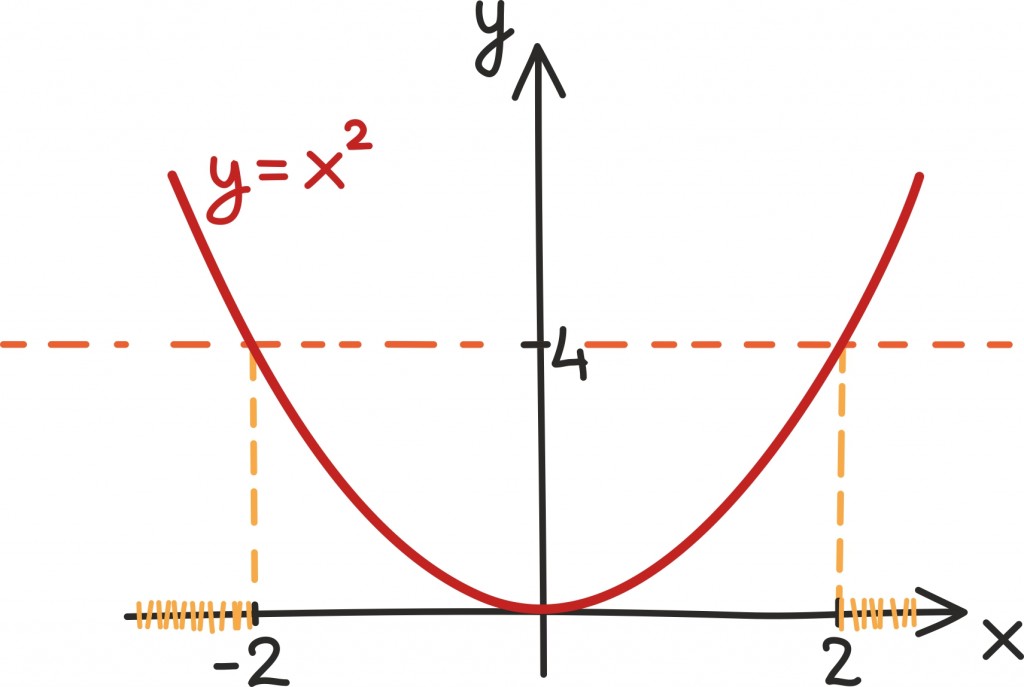
Näiteks kui tahtsime leida arve, mille ruut oli võrdne 4-ga, saime võrrandi: x² = 4. Samamoodi võime otsida arve, mille arvuruut on 4-st suurem. Seda kirjeldab võrratus: x² > 4.

Võrratuste lahendamisel on tihti kasulik mõelda geomeetriliselt – üritame kogu võrratuse taandada mõne funktsiooni graafiku uurimisele.

Ülaltoodud võrratuse korral näeme, et kõik otsitavad arvud peavad olema kas kahest suuremad või miinus kahest väiksemad, sest muudel juhtudel on ruutfunktsiooni y = x² graafik 4-st madalamal.

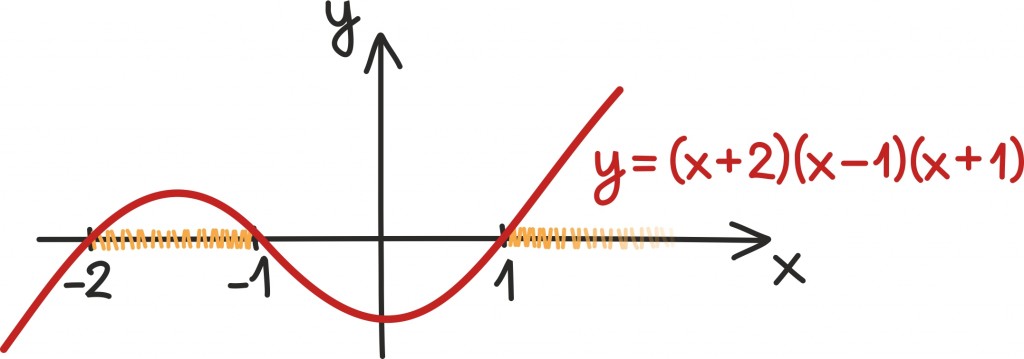
Sama strateegia toimib ka keerulisemate võrratuste puhul. Näiteks oletame, et küsitakse, milliste reaalarvude x jaoks on

Kasutades võrratuse omadusi võime selle võrratuse ümber viia kujusse

Sellises kujus vastab võrratus küsimusele: millal asub kuupfunktsioon x-teljest üleval pool?

Kuupfunktsiooni graafik teeb kokku maksimaalselt kaks pööret, aga sellest räägime pikemalt osa 6 juures [lk 266].

Kuupfunktsiooni oskame umbkaudu joonistada niipea, kui teame ta nullkohti [lk 269]. Seega tegurdame vasemat poolt ja saame samaväärse võrratuse (x + 2) (x – 1) (x + 1) > 0. Nüüd võime vastuse välja lugeda joonistades umbkaudselt kuupfunktsiooni y = (x + 2) (x – 1) (x + 1) graafiku.

Meile sobivad kõik arvud vahemikus (–2, –1) ning kõik ühest suuremad arvud:

Graafiline meetod põhineb sisuliselt funktsioonide graafikute võrdlemisel. Oleksime võinud eelnevalt ka lihtsalt võrrelda funktsioonide x³ + 2x² ja x + 2 graafikuid, aga lihtsam oli teisendada võrratust nii, et üks funktsioon oli kuuppolünoom ja teine lihtne nullfunktsiooni, mille graafikuks on siis x-telg ise.

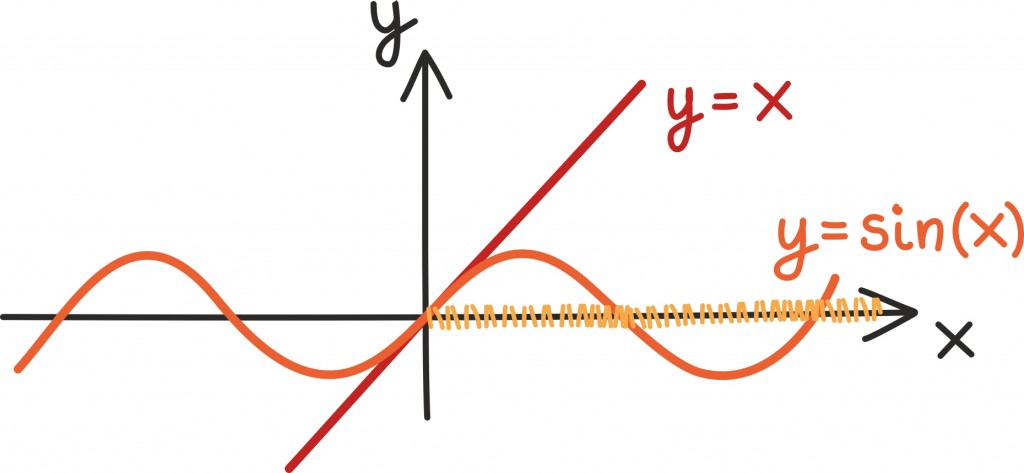
Mõnikord peame aga tõesti joonistama välja kaks erinevat funktsiooni. Näiteks näeme graafikult, et x ≥sin(x) iga mittenegatiivse x-i jaoks.

Selle fakti range tõestus kasutab tuletist [lk 320] ja põhineb täpselt graafikult saadud intuitsioonil: kohal 0 on mõlemad funktsioonid võrdsed ning edasi kasvab funktsioon y = x kiiremini kui funktsioon y = sin(x).

Kuna võrdusjuht on mingis mõttes võrratuse piirjuhuks, võime võrratuste lahendamise taandada tihti võrrandite lahendamisele. Mingis mõttes tegime seda ka kogu eelnenud arutelus: leidsime geomeetriliselt, kus on mingid lõikepunktid, ning otsustasime, kummale poole jäävad siis võrratuse lahendid. Lõikepunktid ise aga tähistasidki võrrandite lahendeid ja piirasid võrratuse lahendite ala. Just selle seose tõttu saime ka tegelikult mobiilioperaatorite küsimusele ainult võrrandite raames vastuse leida.

Võrratuste teisendamine

Võrratustega võib teha peaaegu kõike, mis võrranditegagi. Samaväärsed võrratused saame näiteks, kui

liidame mõlemale võrratuse poolele sama arvu juurde. See on ju igati intuitiivne – kui Sul on rohkem raamatuid kui vennal, on Sul neid rohkem ka pärast seda, kui kirjandushuviline tädi mõlemale teile uue raamatu kingib;
korrutame võrratuse mõlemat poolt sama positiivse arvuga. Ka see on loomulik: perepitsa on suurem kui tavaline pitsa ning ka pool või neljandik perepitsat on suurem kui pool või neljandik tavalisest pitsast.

Siinkohal on oluline märgata, et mõlemaid pooli võib ainult positiivse arvuga läbi korrutada ja mitte negatiivse arvuga. Negatiivse arvu korral tuleb võrratuse märk muuta vastupidiseks. Miks see nii on?

Alustame ühest näitest, võrratusest –3 < 2. Kui mõlemad pooled korrutada läbi –1-ga, saame arvudeks vastavalt 3 ja –2. Kuid enam ei ole 3 väiksem kui 2. Selle välistamiseks pöörame märgi vastupidiseks ning saame, et 3 > –2.

Tähendab ju mõlema võrratuse poole miinus ühega läbi korrutamine tegelikult arvtelje peegeldust 0 punkti suhtes ja nii muutubki võrratuse märk – suurus, mis enne oli arvteljel kõige paremal ning seega suurim, asub pärast peegeldust kõige vasemal ning on seega väikseim.

Kui korrutame võrratuse pooled läbi mõne miinus ühest erineva negatiivse arvuga, nagu näiteks arvuga –4,5, siis võime sellest mõelda kahes sammus: 1) esmalt korrutame mõlemat poolt arvuga –1 ja seega vahetame võrratuse märgi ning 2) seejärel korrutame pooli arvuga 4,5.Muidugi võib ka võrratusega teha teisendusi, mis samaväärsust tingimata ei säilita. Siin tuleb hoolikas olla just sellepärast, et iga kord negatiivse arvuga korrutades võib märk muutuda. Näiteks kui võrratuse mõlemad pooled ruutu võtame, siis saadud võrratus on algsega samaväärne ainult juhul, kui mõlemad võrratuse pooled on positiivsed.Tõepoolest, kui 3 > 2, siis ka 3² > 2². Samas aga –3 < –2, kuid (–3)² > (–2)².

Võrratused ja planeerimine

Matemaatiline planeerimine tegeleb teatud mõttes elulistele probleemidele parimate lahenduste leidmisega. Seejuures on võrratustel matemaatilises planeerimises oluline osa. Toome mõned näited.

Kuidas peaks bussifirma korraldama bussiliiklust, nii et teenida võimalikult palju kasumit? Ühelt poolt tahab bussifirma teha võimalikult vähe kulutusi bussijuhtidele, bussidele ja kütusele. Teiselt poolt peab ta pakkuma võimalikult head teenust, et reisijad ei läheks konkurentide juurde või ei hakkaks sõitma autoga.
Milline on parim istekohtade jaotus klassiruumis, et õpilased oleksid võimalikult õnnelikud? Arvesse tuleb võtta nii õpilaste istekoha- kui ka pinginaabrite eelistusi.
Mida peaks vaene üliõpilane sööma nii, et ta kulutused toidule oleksid võimalikult väiksed, kuid päevased toitainete normid oleksid täidetud?

Järgnevalt vaatame viimast probleemi lähemalt üsna lihtsustatud näite varal, kus tudengi ostukorvi saavad kuuluda vaid kartulid ja oad. Peab tõdema, et päriselt ei taha küll vist keegi ainult kartulitest ja ubadest toituda, aga realistlikumad probleemid on liiga keerulised, et neid paberil ilma arvutite abita lahendada.

Igal juhul alustame oma teadmiste ülesloetlemisega.

Kilo kartuleid maksab 0,7 eurot, sisaldab 20g valke ning 170g süsivesikuid.
Kilo ubasid tomatikastmes maksab 1,4 eurot, sisaldab 60g valke ja 120g süsivesikuid.
Täiskasvanud inimene vajab 50g valke ja 300g süsivesikuid.

Meie küsimus on, millise toidurahaga saab vaene tudeng päevas hakkama ainult kartuleid ja ubasid süües, nii et päeva valkude ja süsivesikute norm oleks täidetud?

Kõigepealt peame selle ülesande tõlkima matemaatika keelde ehk koostama matemaatilise mudeli.

Esmalt leiame koguhinna. Selle jaoks tähistame kartulite kogust kilodes x-iga ning ubade kogust kilodes y-iga. Nii lähevad kartulid maksma 0,7xeurot, oad 1,4y eurot ning mõlemad kokku 0,7x + 1,4y eurot. Tahaksime seda maksumust minimeerida, kusjuures kogustele x ning y on seatud teatud piirangud, mis tulevad päevastest toitainete normidest – peame sööma vähemalt teatud arvu valke ja süsivesikuid.

Üritame nüüd need piirangud võrratuste keeles kirja panna.

Valke on kartulites 20x grammi ja ubades 60ygrammi. Kuna täiskasvanud inimene peaks päevas sööma vähemalt 50 grammi valke, siis saame võrratuse 20x + 60y ≥ 50.

Sarnaselt saame süsivesikute jaoks tingimuse 170x + 120y ≥ 300.

Lisaks ei saa ei kartulite ega ubade kogused olla negatiivsed arvud. Seetõttu on meil veel võrratused x≥ 0 ja y ≥ 0

Oleme saanud järgneva matemaatilise mudeli. „min” tähendab siin, et otsime võrrandi väikseimat ehk minimaalset väärtust ning muidugi peavad lisaks olema rahuldatud kõik toodud võrratused:

Seda ülesannet on kõige lihtsam lahendada graafiliselt. Selleks kanname koordinaatteljestikku kõik neli võrratust ning märgime ära piirkonna, mis kõiki võrratusi rahuldab.

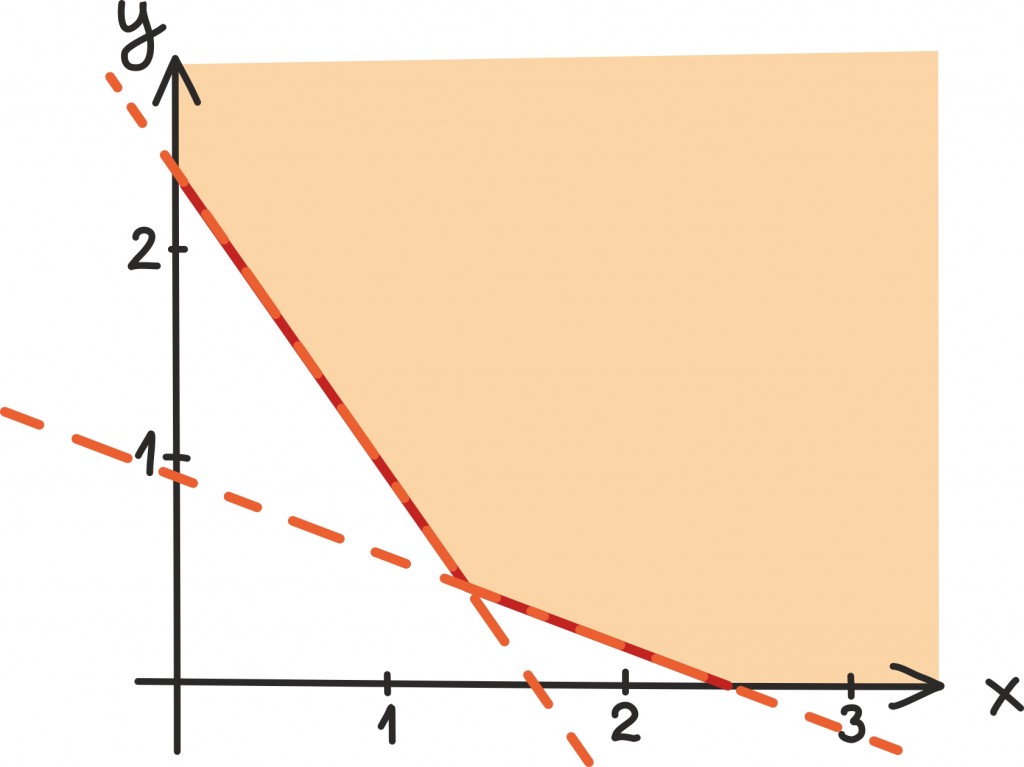
Viimaks leiame märgistatud piirkonnas punkti, kus funktsiooni 0,7x + 1,4y väärtus on minimaalne. Kuidas seda teha?

Meenutame, et sirged kujus 0,7x + 1,4y = c on kõik omavahel paralleelsed ning vähendades c väärtust, liigutame seda sirget lihtsalt allapoole. Nüüd asub 0,7x + 1,4y minimaalne väärtus kindlasti ühel sellistest sirgetest ning lahendiks on paar (x, y) täpselt siis, kui ta ka omakorda lahendipiirkonda jääb. Seega on meie ülesanne leida minimaalne c väärtus, mille korral sirge 0,7x + 1,4y = c lõikab veel endiselt lahendipiirkonda.

Nagu jooniselt näeme, juhtub see täpselt sirgete 20x+ 60y = 50 ja 170x + 120y = 130 lõikumispunktis, mida oskame juba lihtsalt leida: 1,54 kg kartuleid ja 0,32 kg ubasid lähevad maksma 1,53 eurot.

Mõned levinud võrratused

Nii nagu koolist on hästi teada, et õpetaja on alati targem kui õpilane, kehtivad ka teatud võrratused väga paljude erinevate arvude või elementide jaoks. Näiteks kehtivad mõned võrratused absoluutselt kõikide positiivsete reaalarvude jaoks või kõikide ühest suuremate reaalarvude jaoks või kõikvõimalike kolmnurkade jaoks. Loetleme ja selgitame neist siinkohal mõnda.

Reaalarvu ruut

Kõige tuntum võrratus on ilmselt järgmine: iga reaalarvu ruut on mittenegatiivne ehk a² ≥ 0. Võrdus kehtib muidugi parajasti juhul, kui a on võrdne nulliga. Miks see ikkagi on nii?

Nulli puhul on muidugi asi selge, on ju nulli ruut jällegi null.

Ka positiivsete arvude puhul pole asi palju keerulisem: a² on ju täpselt küljega a ruudu pindala ning ruudu pindala peabki positiivne olema.

Iga negatiivse arvu võime aga kirjutada kujul –a = (–1) · a, kus a on ise positiivne. Sel juhul võime kirjutada

ning tulemus on jällegi positiivne.

Kumb on suurem, arv või tema ruut?

Võibolla kõlab see alguses natuke mitteintuitiivselt, aga arvu ruut ei ole mitte sugugi alati suurem kui arv ise. Negatiivse arvu ruut on muidugi alati temast suurem, sest eelneva põhjal on arvuruut ise alati positiivne.

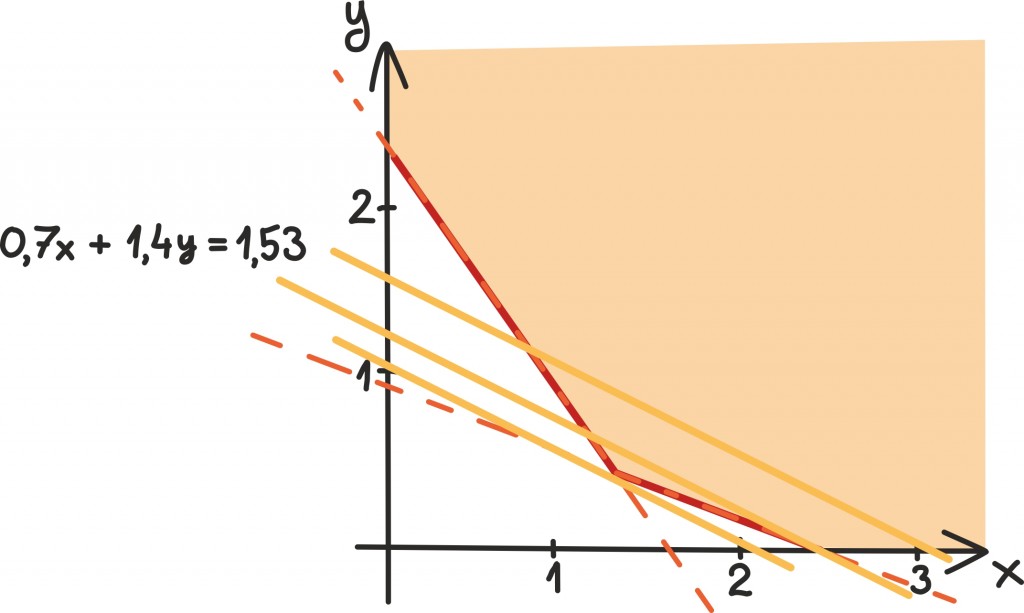
Samuti, kui positiivne reaalarv on ühest suurem, siis on ta ruut arvust suurem. Kui aga positiivne reaalarv on ühest väiksem, siis on ta ruut arvust väiksem:

Ka seda pole väga raske tõestada – teame ju, et võime iga võrratust positiivse täisarvuga läbi korrutada:

korrutades võrratuses a >1 mõlemad pooled a-ga, saame võrratuse a²> a,
korrutades võrratuses a < 1 mõlemad pooled a-ga, saame võrratuse a² < a.

Aritmeetiline ja geomeetriline keskmine

Arvude aritmeetiline keskmine tuleb esile üsna tihti: näiteks arvutatakse välja keskmist hinnet, eksamitulemuste keskmist või rahva keskmist vanust. Selle jaoks liidetakse lihtsalt kõik uuritavad tulemused kokku ja jagatakse summa tulemuste arvuga:

Keskmistada võib aga teisiti: võib kõik tulemused kokku korrutada ning siis võtta nendest nii mitmes juur, kui palju tulemusi oli.

Geomeetriline keskmine tuleb esile näiteks televiisorite kuvasuhete määramises. Vana kinostandard oli kuvasuhe 2,39:1 (pilt on 2,39 korda laiem) ning vana televiisor näitas filme suhtes 4:3. Nende kahe standardi vahel kompromissi leidmiseks kasutati geomeetrilist keskmist ning saadi tulemuseks 16:9 standard. Geomeetrilise keskmise kasutamine võimaldas saavutada olukorra, kus mõlemaid proportsioone „muudeti” ühepalju.

Nii aritmeetiline kui geomeetriline keskmine on ka seotud vastavanimeliste jadadega [lk 128]. Nimelt on aritmeetilise jada kolmest järjestikusest liikmest keskmine äärmiste aritmeetiliseks keskmiseks ning täpselt sama juhtub ka geomeetrilises jadas, kasutades geomeetrilist keskmist.

Üks tuntud võrratus väidab, et kahe mittenegatiivse reaalarvu aritmeetiline keskmine on vähemalt sama suur kui kahe arvu geomeetriline keskmine. Ehk:

Kuidas seda tõestada?

Vaatame arvu

Kuna tegemist on arvuruuduga, siis on ta mittenegatiivne. Avades sulud, saame

ehk tõesti

Graafiliselt võib aritmeetilisest ja geomeetrilisest keskmisest ning nendevahelisest võrratusest mõelda järgnevalt:

Tõestus vajaks natuke kolmnurkade ja trigonomeetriaga mängimist. Huvitunud lugeja võib seda proovida näiteks peale trigonomeetria peatüki läbimist [lk 205].

Kuigi meie tõestasime siin ainult, et kahe arvu aritmeetiline keskmine on suurem geomeetrilisest keskmisest, siis tegelikult kehtib väide mistahes paljude arvude kohta. Suvalise mittenegatiivse arvu aritmeetiline keskmine on suurem kui geomeetriline keskmine. Seda on siiski juba pisut keerulisem tõestada.

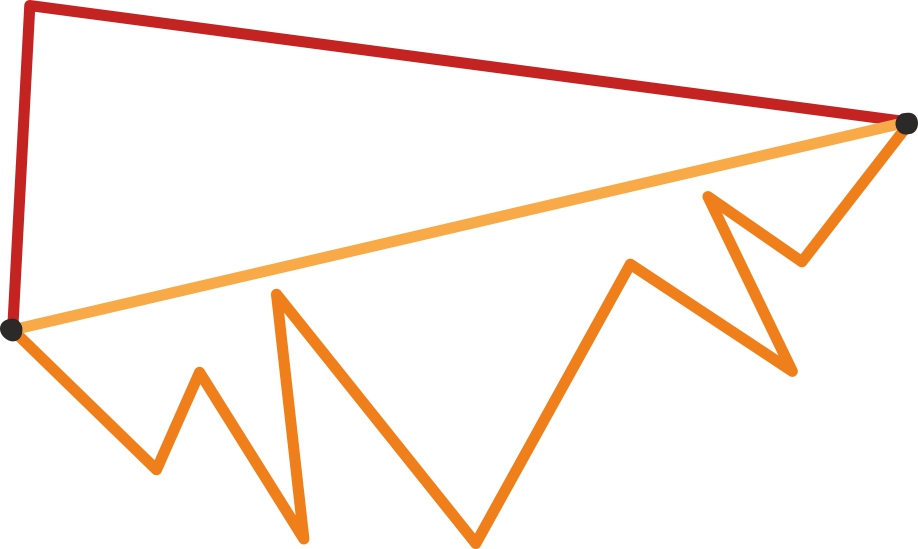
Lühim murdjoon

Lõpetame peatüki ühe väga lihtsa geomeetrilise võrratusega. See väidab, et kahe punkti vahelistest murdjoontest on vähima pikkusega neid punkte ühendav sirglõik.

Sellest võrratusest järeldub kohe näiteks tuntud kolmnurga võrratus: kolmnurga iga kahe küljepikkuse summa on pikem kui kolmas külg. See lihtne väide osutub järelikult üsna sisukaks.

Absoluutväärtusega võrrand