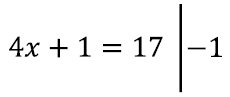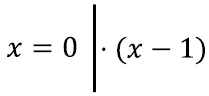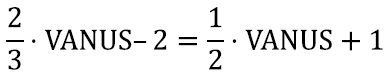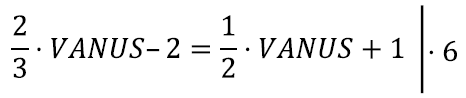Võrrandi teisendamine ja lahendamine

Enamasti on võrrandi kirjapanek alles esimene samm. Järgneb võrrandi lahendamine: see tähendab, et tahame leida kõik arvud, mis kõiki võrrandiga ette kirjutatud tingimusi rahuldavad.Võrrandi lahendamise ajaks võib kõikide võrrandi liikmete ühikud ja konteksti ära unustada – võrrandi lahendamise ajal ei loe, kust see võrrand tuli, loeb vaid matemaatika.Võrrandi tõlgendamisel tuleb muidugi lisada jälle juurde ka kontekst ja ühikud. Siis seome taas elu matemaatikaga ja see vajab palju tähelepanu, sest tihti tekivad vead just selles etapis.Praegu asume aga lahendamise juurde. Alustame võrrandi teisendamise matemaatilisest küljest ja seejärel teeme kogu protsessi läbi veel ühe konkreetse luguloo taustal.

Võrrandi teisendamisest üldiselt

Niipea kui võrrand on kirja saanud, on eesmärk seda lahendada. See toimub tihti võrrandi teisendamise abil. Võrrandi teisendamine tähendab võrrandi viimist teise, ent siiski samaväärsesse kujusse. Ideaalselt jõuame võrrandiga kujusse, kust on vastust juba kerge välja lugeda.

Kõik teisendused, mis pähe tulevad, ei säilita muidugi võrrandi samaväärsust: näiteks kui korrutame mõlemad pooled arvuga null, siis saame mõlemale poole võrdusmärki nulli. Null on aga nulliga võrdne, ükskõik millise väärtuse me algsele muutujale ka annaksime.

Kõige lihtsam viis võrrandi erinevate kujude samaväärsuse näitamiseks on veenduda, et võime võrrandi uuest kujust mõne teise sammu abil jälle võrrandi algsesse kujusse tagasi jõuda.

Näiteks võime võrrandile alati arve liita, sest vastandarvude liitmine teisendaks uue võrrandi jälle tema algkujusse. Nii on näiteks samaväärsed võrrandid

Esimesest saame teise kahte lahutades, teisest esimese kahte juurde liites.

Samamoodi võime võrrandeid nullist erineva arvuga korrutada, kuna sama arvuga jagamine (sellest siis ka nullist erinevus!) viiks võrrandi taas algkujusse tagasi. Nii on samaväärsed ka võrrandid

Esimesest saame teise pooli neljaga jagades ning teisest esimese, kui mõlemat poolt neljaga korrutame.

Neid kahte teisendust järjepanu tehes näeme, et võrrand 4 · x + 2 = 10 on samaväärne võrrandiga x = 2. Ehk teisisõnu selle esimese võrrandi lahendiks on x= 2.

Vaatame igaks juhul veel teistki näidet – sisu ja soustita võrrandit 4x + 1 = 17. Tema lahenduskäigu saame kompaktselt kirja panna nii:

Siin oleme püstkriipsu taha lihtsalt märkinud, mida täpselt teeme ühelt realt järgnevale üleminekuks, kõik need on samaväärsed teisendused.

Tihti on võrrandi teisendamisel samaväärsust säilitavatel sammudel ka hea intuitiivne selgitus:

näiteks võime võrrandi mõlemale poole juurde liita arve. Intuitiivselt on see selge: kui meil on täna sõbraga sama vanus, siis on meil ka täpselt kahe aasta pärast sama vanus;
samuti võime võrrandi mõlemaid pooli korrutada suvalise nullist erineva arvuga – kui oleme praegu võrdses kaalus, oleksime ka siis, kui meie mõlema kaalud kolmekordistuksid. (Loodame siiski, et seda ei juhtu.)

Kõik teisendused aga samaväärsust ei säilita.

Sulle võivad huvi pakkuda need õppematerjalid:

Võrrandi teisendamine nii, et samaväärsus ei säili

Võrrandit saab muidugi teisendada ka nii, et uus võrrand ei ole päris samaväärne. Sel juhul võib võrrandile uusi lahendeid juurde tekkida või ära kaduda – mõne teisenduse korral muudame lihtsalt võrrandi algset tingimust väetimaks ja mõnikord lisame hoopis juurde väärinformatsiooni.

Näiteks kui korrutame võrrandi mõlemat poolt 0-ga, kaotame ju kohe kogu tingimusega antud informatsiooni, sest pärast seda on mõlemad võrrandi pooled võrdsed 0-ga ning see võrdus kehtib iga muutuja väärtuse jaoks.

Samamoodi võime ruutu võttes lahendeid juurde tekitada: öelda, et x = 3, annab täpselt ühe vastuse, aga x² = 9 juba kaks vastust, kuna teist võrrandit rahuldab ka x = –3.

Üldiselt ei tasu sellepärast aga väga muretseda – teisendage võrrandit mõnuga, kuni oskate temast midagi välja lugeda. Pärast tuleb lihtsalt üle kontrollida, kas saadud lahendid ka algseid tingimusi rahuldavad või on kaasa tulnud teisendustega kaasnenud informatsiooni kao käigus. Ettevaatlik ja hoolas tasub siiski olla.

Tõestus, et 0 = 1, ehk miks võrrandi teisendamisel tuleb ette vaadata.

Kirjutame välja üsna sisutühja võrrandi x = 0 ja hakkame teda põnevuse tekitamiseks teisendama.

korrutame mõlemaid võrrandi pooli

avame sulud

liidame mõlemale poole liikme x

jagame x-iga läbi

saame uue vastuse

Aga kui me nüüd vaatame ühes algset võrrandit x = 0 ning viimast võrrandit x = 1, siis saame, et sama arv x on võrdne nii nulli kui ühega, ja peame järeldama, et 1 = 0!

Ometigi teame, et see on jaburus ning algne võrrand x = 0 ei ole samaväärne viimase võrrandiga x= 1.

Seega peame tee peal olema kasutanud mõnda algtingimusi väänavat teisendust. Tõepoolest, vaadates üleminekut sammult 4 sammule 5, oleme võrrandi mõlemat poolt läbi jaganud x-iga. Ent x on ju võrdne nulliga ning nulliga jagamine toobki alati ainult jama kaasa!

Väike võrrandijutt

Nüüd aga aitab hetkeks puhtast matemaatikast, lähme pimekohtingule ja vaatame, kas kõik sai selgeks.

Juba joomegi meile üsna mokkamööda seltsilisega koos kohvi, sööme kooki, naeratame ja tutvume. Küsime kaaslaselt ka piinlikkust tundmata vanust. Ent mis juhtub? Kaaslane hakkab vastu õhtut kiusama ja vigurdama!

Ta sõnab muiates, et kui võtta tema vanusest kaks kolmandikku ja lahutada sealt kaks, saate sama tulemuse, kui võtta tema vanusest pool ja liita sinna üks. Milline õudus, kaaslane tahab teada, kas oskame võrrandeid koostada ja neid lahendada!

Võtame väljakutse vastu! Taskust välja salvrätt, ja kaaslase avaldused lähevad sinise tindiga hoolikalt kirja. Teisisõnu, koostame elulise loo põhjal võrrandi.

Võrrandi koostamine

Ainsaks tundmatuks on kaaslase vanus, mida alguses kirjeldamegi muutujaga VANUS. Tema sõnades järge ajades võime kirjutada:

Nüüdseks on meil kõik tingimused kirjas ning edasi on meie töö võrrand ka ära lahendada.

.

Võrrandi lahendamine

Kaaslase vanuse väljalugemiseks võime oma võrrandit näiteks teisendada järgmiselt:

(kellele meeldiksid murrud, saagem neist lahti!)

(tahame leida vanust, lahutame mõlemalt poolt 3 · VANUS viies kõik tema kordsed ühele poolele)

(liidame, lahutame)

Hurrraa, matemaatiline osa on läbi!

Ja siinkohal vist suurt midagi ka jäänud pole. Võrrandi lahendi tõlgendamine pole eriti raske – isegi muutuja nime jätsime selliseks, mis päriselulist mõtet kenasti kaasas kannab.

Veel võrrandi lahendamisest

Siin alapeatükis ründame kahte küsimust: mida ikkagi peame silmas võrrandi lahendamise all ning miks seda üldse õppima peaks.

Võrrandi lahendamine erinevates arvuhulkades

Seni oleme rääkinud, et võrrandi lahendamine tähendab teatud tingimusi täitvate arvude leidmist. Matemaatiliselt pole see mitmel põhjusel päris täpne kirjeldus.

Näiteks oleme jätnud mainimata, milliseid arve silmas peame. Ometigi nägime arvuhulkade peatükis [lk 78], et leidub mitu erinevat arvude hulka. Seega kui räägime arvude leidmisest, kas mõtleme naturaalarve, täisarve, reaalarve, kompleks-arve?

Kui kirjeldame võrrandi abil mõnda elulist olukorda, määrab seesama olukord lahenditele antavad tingimused.

Näiteks kui meil on otsitavaks muutujaks inimeste arv, oleks tore, kui tegemist oleks naturaalarvuga. Samuti oleks meid üllatanud, kui kaaslase vanus oleks osutunud nullist väiksemaks. Samas kui otsitavaks on sõbra sõidukiirus, võiks see vabalt olla mistahes positiivne reaalarv.

Kui lahendame võrrandeid oma lõbuks, võime täiesti ise otsustada, milliste arvudega ennast piirame. Näiteks kahe muutujaga lineaarvõrrandi korral on mõistlik end piirata reaalarvudega – nii saame ilusa vastavuse sirgetega tasandil [lk 184].

Ka ruutvõrrandi korral piirame end reaalarvudega [lk 87], kui tahame joonistada ilusat graafikut, ja samas võtame arvesse ka kompleksarvud [lk 89], kui soovime lahendit leida igale võimalikule ruutvõrrandile.

Üldiselt kehtibki, et mida rohkem arve endale lubame, seda rohkem lahendeid võime ka leida. Näiteks võrrandil x² = 2 puuduvad lahendid ratsionaalarvudes, ent ometi eksisteerivad nad juba irratsionaalarvude hulgas. Võrrandil x⁴ = –1 ei leidu lahendeid reaalarvude hulgas, aga neid on täpselt neli, kasutades kompleksarve.

Võrrandite lahendamine erinevates arvuhulkades on väga erineva raskusega. Näiteks ei ole mingit raskust lahendada kolme muutujaga võrrandit X¹⁰ + Y¹⁰ =Z¹⁰ kompleksarvudes – nimelt igale X-i ja Y-i kompleksarvulisele väärtusele saame leida kompleksarvulisi Z-i väärtusi täpselt 10.

Täisarvudes suudeti seesama võrrand aga lahendada alles pärast kolmesaja-aastast pingutust – positiivsetes täisarvudes ühtegi lahendit ei leidugi!

Teoreemi, mis väidab, et kui n on kahest suurem täisarv, siis ühelgi võrrandil kujus

positiivsetes täisarvudes lahendit ei leidu, kutsutakse Fermat’ suureks teoreemiks.

Teoreemi nimi on antud 17. sajandi prantsuse matemaatiku Pierre de Fermat’ järgi. Ta oli küll ametilt jurist, aga vabal ajal tegeles kõige meelsamini just matemaatikaga. Ta mõtles põhjalikult küsimusele, millal ikkagi ülaltoodud võrrandi lahendid leiduvad, ning ühe paberilehe äärel väitis ka, et tal on lihtne tõestus, mis näitab, et juhul kui on kahest suurem täisarv, täisarvulisi lahendeid ei leidugi. Seda tõestust aga keegi tema paberitest leidnud pole ning pole keegi suutnud lihtsat tõestust ka välja mõelda.

Tänaseks on küll Fermat’ suur teoreem tõestatud, kuid lahendus laiutab üle paarisaja lehekülje ning on matemaatiliselt ikka parajalt keeruline.

Miks võrrandeid lahendada?

Isegi kui arvutid ei oska elu võrranditesse panna, on nad tingimata head võrrandite lahendamisel. Neile tuleb lihtsalt võrrand ja mõned lahendusnipid ette sööta ning jääda vastuseid ootama.

Näiteks kasutades maatriksesitlust [lk 152], võib arvutitele anda täpse algoritmi, mille abil võivad nad iga lineaarvõrrandisüsteemi täpselt ja kiiresti lahendada. Sadade muutujate ja lineaarvõrranditega võrrandisüsteem võtab arvutil aega ainult hetke.

Võib tekkida küsimus: miks siis üldse ise õppida nende lahendamist?

Esiteks, kuna meid ei huvita mitte ainult võrrand ise, vaid ka tema eluline kontekst, siis võib ka võrrandi lahendamine anda ideid sellesama konteksti kohta. Nii mõnigi kord saame lahendussamme ka eluliselt tõlgendada ja sellest kasugi saada.

Teiseks annab võrrandite lahendamine oskused matemaatiliste tehetega möllamiseks, mida tuleb ette mujalgi, kus elu matemaatikasse lööme.

Viimaks, paljude kõrgema astme võrrandite lahendamise jaoks ei leidu (veel) täpseid retsepte, mida arvutile ette sööta – nende lahendamine vajab tõepoolest nupukust. Näiteks on teada, et võrrandilx² – 2y³ = 58 leidub lahendeid, neid kõiki leida aga arvuti ei oska. Ja ka kõik praegused retseptid, mida arvutid kasutavad, tulenevad just varasemate matemaatikute mõttetööst – ka sellele tahab ehk mõni lugeja ükspäev kaasa aidata.

Võrrand ja geomeetria