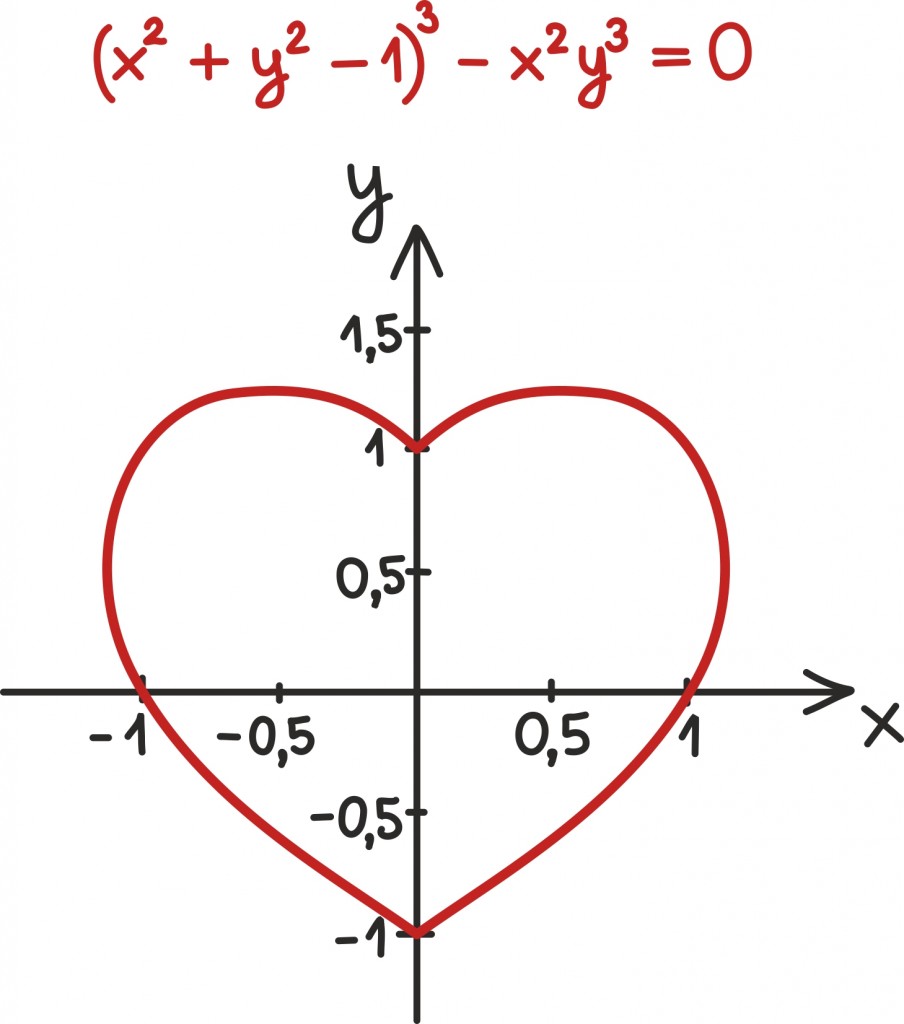
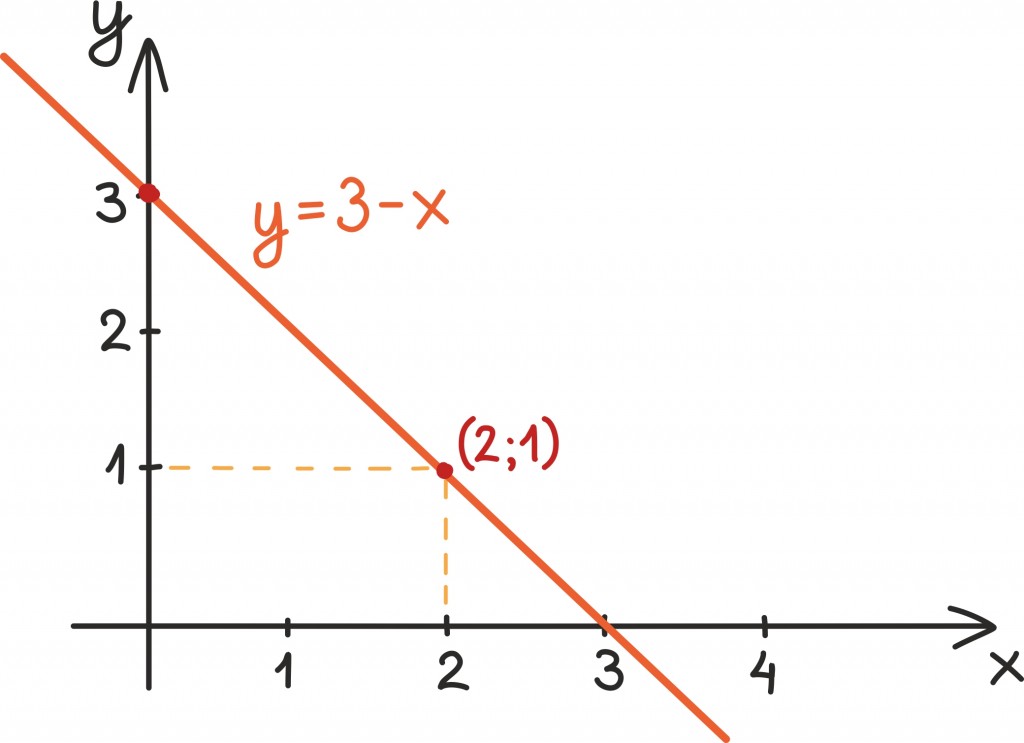Võrrand ja geomeetria

Mõni muutujarägastikuga võrrand võib alguses üsna eemaletõukav tunduda. Kuid ühte ilusti tõmmatud kõverat, mis väljendab sedasama võrrandit, on alati kaunis vaadata.

Õnneks tuli 16. sajandil prantsuse matemaatik ja filosoof Descartes selle peale, kuidas omavahel võrrandeid ja geomeetriat siduda.

Kõige lihtsam seos on kahe muutujaga lineaarvõrrandite ja sirgete ning kolme muutujaga lineaarvõrrandite ja tasandite vahel. Nendest seostest pajatame ka käesolevas peatükis.

Võrrandi ja geomeetria vaheline tõlkimine

Võrrandil x + 2 = 3 on muutujale antud väga karmid tingimused ning võimalik on täpselt üks lahend: xpeab olema võrdne ühega. Geomeetriliselt võime sellest võrrandist mõelda kui sellise arvtelje punkti leidmisest, mis on arvust 3 kahe ühiku võrra vasemal.

Üks viis tingimusi väetimaks muuta ja võrrandile rohkem lahendeid tekitada, on mängu tuua rohkem muutujaid. Näiteks võrrandil x + y = 3 on lahendeid maa ja ilm: iga y-i väärtuse jaoks leidub sobiv väärtus ka x-ile. Kui y on võrdne 2-ga, peab x olema võrdne ühega. Kui y on võrdne 3-ga, peab x võrduma nulliga ja nii edasi.

Kõik võrrandi x + y = 3 lahendid on antud arvupaaridena – üks neist ütleb võimaliku muutuja yväärtuse ja teine muutuja x väärtuse. Iga selline arvupaar tähistab aga täpselt ühte punkti arvutasandil: x-i väärtus annab punkti x-koordinaadi ning y-i väärtus punkti y-koordinaadi.

Kui hakkame kõiki neid punkte joonistama, näeme, et nad otsustavad kõik ennast kenasti ühele sirgele ritta seada.

Selgub, et iga kahe muutujaga lineaarne võrrand (mõlema muutuja aste on üks) kirjeldabki täpselt ühte sirget tasandil ja vastupidi ka: kui meile on antud üks sirge tasandil, võime kirjeldada teda kahe muutujaga lineaarse võrrandi abil.

Kõikvõimalikud sirged tasandil oskame kergesti joonistada, kõikvõimalikud kahe muutujaga lineaarvõrrandid on aga antud järgmise kujuga:

Siin on a, b lihtsalt suvalised reaalarvulised kordajad ning c reaalarvuline vabaliige.

See seos on päris kihvt! Meil on ühelt poolt midagi geomeetrilist, joon, mida võime pliiatsi või pastakaga paberile vedada, ning teiselt poolt kuivana näiv võrrand ja ometigi kirjeldavad mõlemad sama matemaatilist objekti!

Ka praktilisema poole pealt on see seos vägagi kasulik, kuna võimaldab tingimusi ja seoseid kirjeldada nii geomeetria kui võrrandite keeles. Seega kui sirgel on mõni omadus, siis peab see vastav omadus olema kirjeldatav ka võrrandite keeles ja vastupidi.

Oletame näiteks, et meie geomeetriliseks omaduseks on teadmine, et sirge läbib punkti null. Milline oleks see omadus võrrandite keeles?

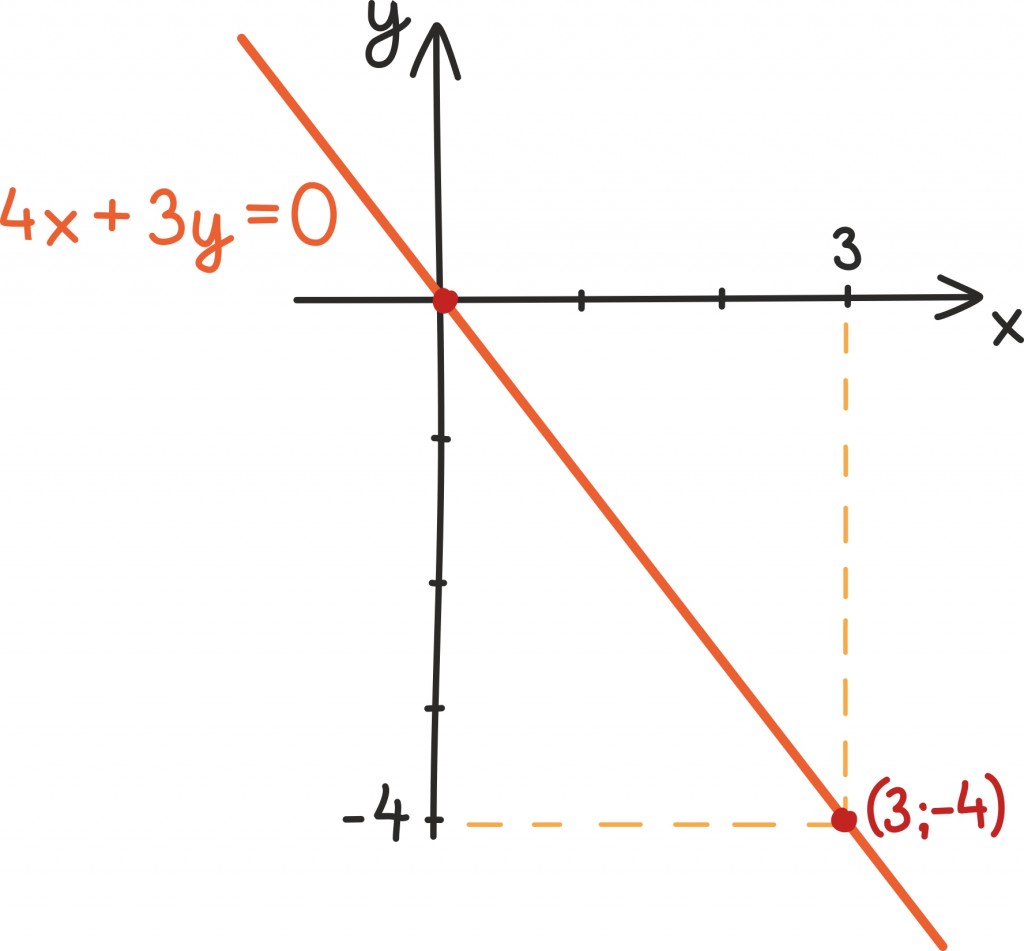
Kui sirge läbib punkti null, siis rahuldab arvupaar (0; 0) võrrandi tingimusi. Sisestades x = 0 ja y = 0 võrrandi üldkujusse, saame, et 0 = c. Seega kui sirge läbib punkti null, puudub vastaval võrrandil vabaliige ning sellise võrrandi võib kirja panna kujul ax + by = 0. Näiteks joonistatud sirge võrrand on 4x + 3y = 0

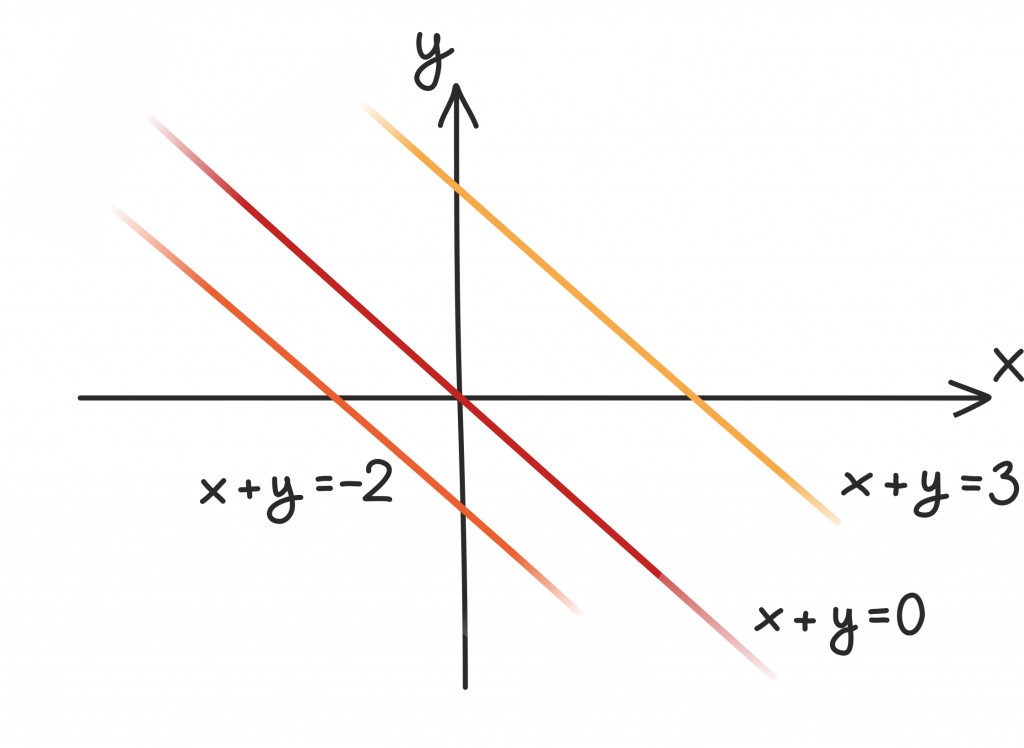
Lähtudes võrrandite keelest võiksime aga küsida: millised sirged vastavad võrranditele kujus x + y = cmingi suvalise arvu c jaoks?

Joonistades võib veenduda, et kõik need sirged on kenasti paralleelsed.

Nii nagu iga kahe muutujaga lineaarne võrrand on täpselt vastavuses mõne tasandi sirgega, on iga kolme muutujaga lineaarne võrrand ilusas vastavuses mõne tasandiga kolmemõõtmelises ruumis.

Ka siin võime geomeetrilisi omadusi kirjeldada võrrandite keeles ja vastupidi. Näiteks võrrandid kujus ax + by + cz = 0 kirjeldavad kõik tasandeid, mis läbivad koordinaatteljestiku nullpunkti. Kõike seda on muidugi juba palju keerulisem joonistada

Sulle võivad huvi pakkuda need õppematerjalid:

Sirgete lõikumine tasandil ja vastav võrrandisüsteem

Nagu nägime, on iga sirge tasandil vastavuses ühe lineaarvõrrandiga kujus ax + by = c. Seeläbi on sirgete omaduste kirjeldamine võrdväärne lineaarvõrrandi kirjeldamisega.

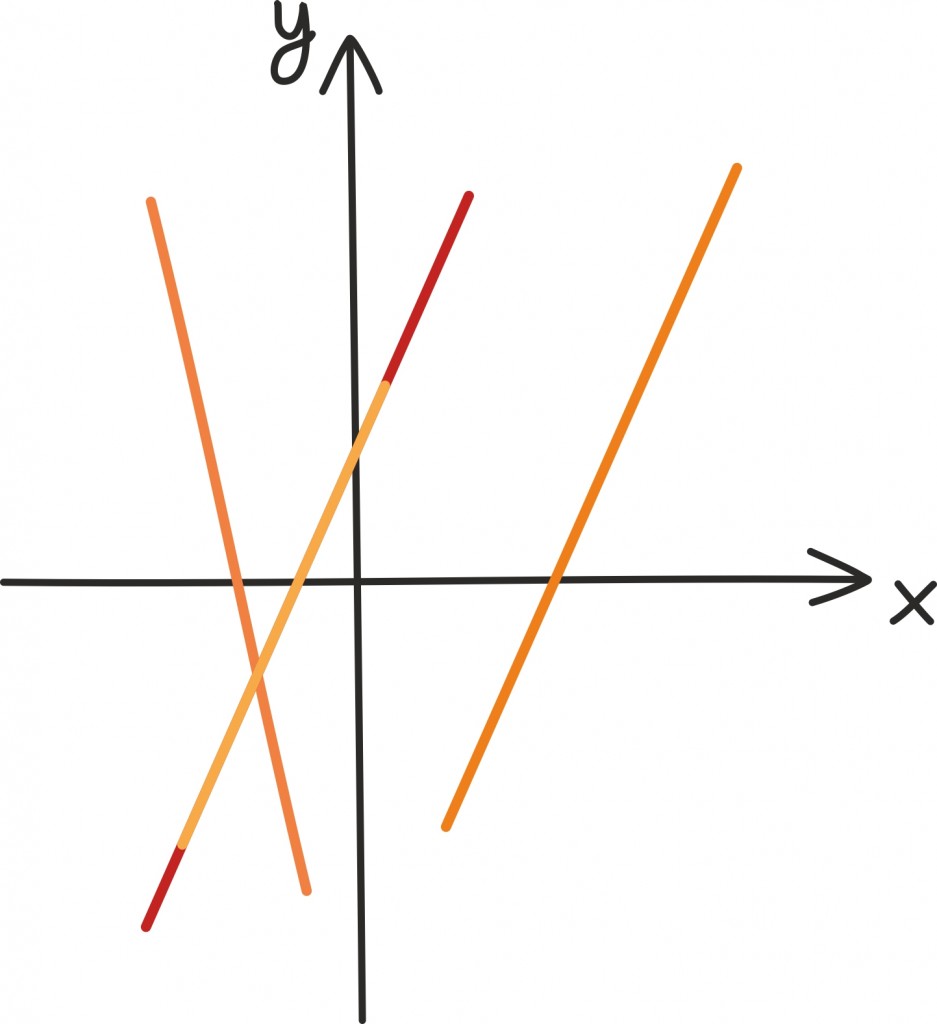
Olukord muutub veelgi põnevamaks, kui tasandile asetada neid mitu. Kui meil on kaks sirget, tekib ju mitmeid geomeetrilisi võimalusi nende kahe sirge suhestumiseks. Kaks sirget võivad kas

lõikuda ühes punktis,
olla paralleelsed,
või kattuda.

Samaaegselt võime mõlemat sirget aga kirjeldada ka kahe muutujaga lineaarse võrrandiga. Mis kirjeldab nende võrrandite omavahelist suhestumist?Selleks on muidugi neist kahest võrrandist koosnev võrrandisüsteem!Tõepoolest, võrrandisüsteem otsib ju kõiki punkte, mis rahuldavad mõlemat sirge võrrandit ühtaegu, ehk teisisõnu kõiki punkte, mis asuvad korraga nii ühel kui teisel sirgel.Neid punkte on

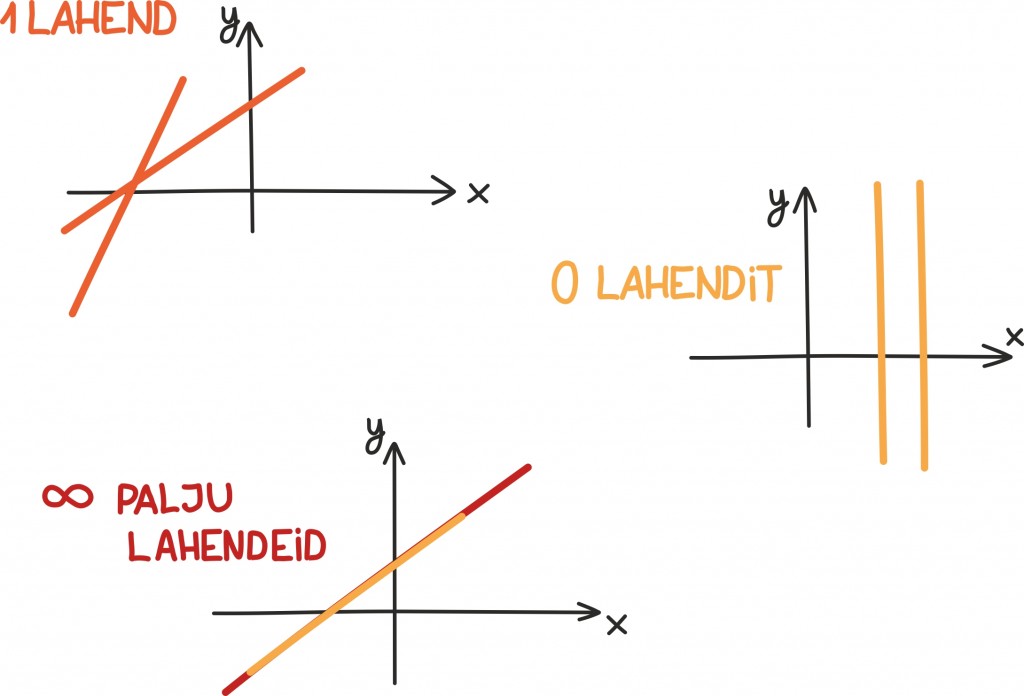
täpselt üks, kui sirged lõikuvad,
null, kui sirged on paralleelsed,
lõpmatult palju, kui mõlemad sirged on üks ja sama sirge.

Nii saamegi võrrandisüsteemi lahendamisega täpselt teada, kuidas nende võrranditega kirjeldatud sirged omavahel asetsevad.

Sirgete ja tasandite rakendused

Sirgete ja tasandite võrrandid, nende koostamine ja nendega mängimine kuuluvad väheste lemmikhobide kilda. Siiski tasub nendega hästi läbi saada juba näiteks sellepärast, et nad mängivad täiesti arvestatavat rolli arvutigraafikas.

Näiteks võivad sirge ja tasandi võrrandid ette tulla arvutimängude loomisel.

Kujutame ette, et arvutimängus on kolmemõõtmeline tuba. Ühes seinas on aken, millest paistab sisse ilus päevane valgus. Mõni päikesekiir levib kenasti sirgjooneliselt ning muidugi otse vastu põrandat, millest võime mõelda kui tasandist. Valguskiire levikut kirjeldab seega sirge võrrand ja põrandat tasandi võrrand.

Kuid päris elus ei jää valgus lihtsalt põrandale, vaid peegeldub sealt edasi. Sellepärast tulebki iga sellise valguskiire ehk sirge jaoks välja arvutada tema peegelduse järgne suund ning seega jälle uus sirge. Muidugi ei piirdu valguskiir ainult ühe peegeldusega, vaid levib ja peegeldub järjest edasi seintelt, laelt, mööblilt. Nii tuleb korduvalt välja arvutada sirgete ja tasandite võrrandeid.

Õnneks ei pea me seda ise tegema – tuleb lihtsalt arvutile õpetada, kuidas arvutamine käib, ja edasi teeb ta kõiki neid tehteid meeletu kiiruse ja täpsusega.

Päris lõpmatult valguskiiri siiski põrgatama ei pea. Pärast sadat põrget on toas juba kenasti eri toonides seinad, pehmete servadega varjud ja kõik muu, mis tekitab meile hea koduse tunde. Oleme arvutile päriselu selgeks teinud ja meie mäng näeb realistlik välja.

Võrratus