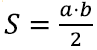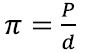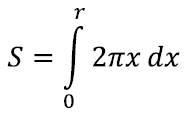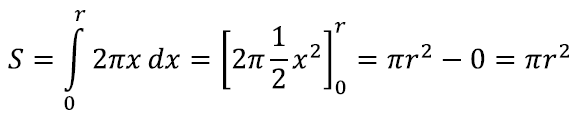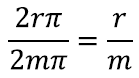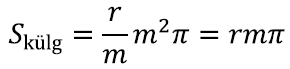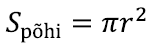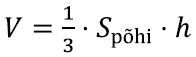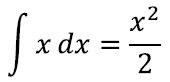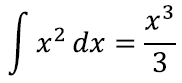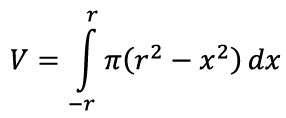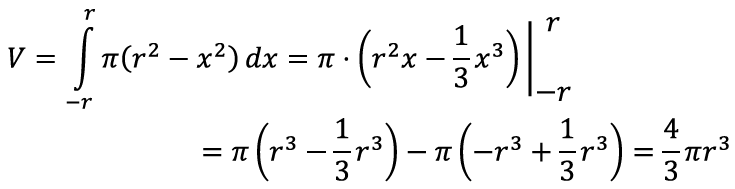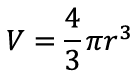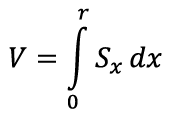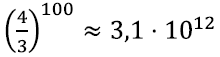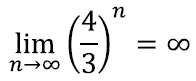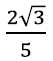Ümbermõõt, pindala ja ruumala
Matemaatilised etalonid: sirglõik, ruut, kuup
Ümbermõõdu või joonepikkuse mõõtmiseks on meil varnast võtta suur hulk häid mõõdutükke: pisikesed sirglõigud erinevate pikkustega. Ilmselgelt piisab neist, et mõõta iga sirglõikudest koosneva murdjoone pikkust:
Aga tegelikult ei valmista muret ka kõverjooned, kui oleme nõus väikest viga sallima: nimelt jagades kõverjoone väga pisikesteks tükkideks on iga tükk peaaegu sirgjoon:
Sellisele lähendamisele annab matemaatilise tähenduse integreerimine [lk 340] ja tuleme selle juurde veel hiljem tagasi.
Pindalade leidmisel valime samuti kõige lihtsama võimalikest etalonikomplektidest: erineva küljepikkusega ruudud. Esmalt peaksime end aga veenma, et teame iga etaloni enda pindala.
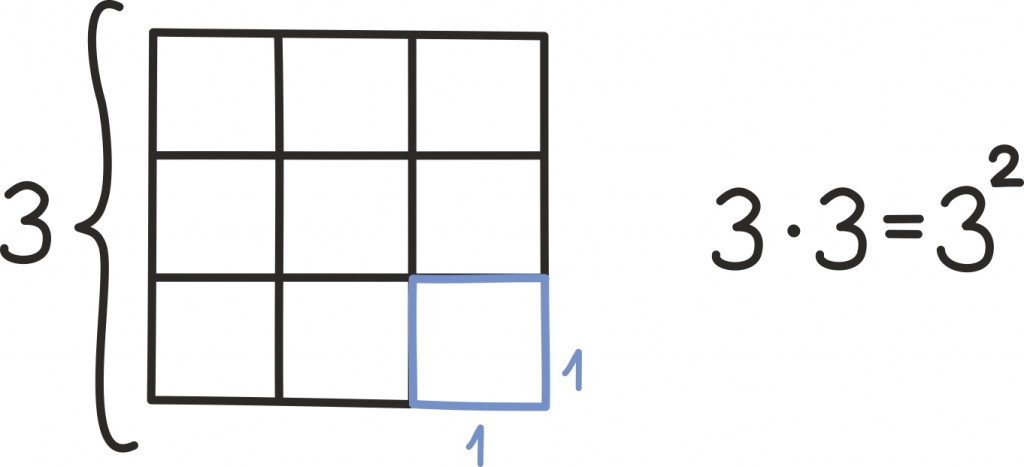
Õnneks pole see väga keeruline: niipea kui teame, et näiteks ühikruudu pindala on 1, võime teisi ruute võrrelda ühikruuduga ja joonis aitab meil veenduda, et küljepikkus a annab pindalaks a2:
Matemaatilise tõestuse tarvis peaks muidugi olema pisut hoolikam.
- Naturaalarvuliste küljepikkustega ruutude jaoks võime kasutada joonisel toodud strateegiat.
- Naturaalarvude pöördarvude
jaoks kasutame joonisel toodud strateegiat vastupidi: täidame ühikruudu ruudukestega küljepikkusega
- Kasutades nüüd seda teadmist, võime jällegi joonist järgides leida pindala kõikide ratsionaalarvuliste küljepikkuste
jaoks.
- Viimaks peame midagi tegema ka irratsionaalarvuliste küljepikkustega. Siin on tarvilik pisut teistmoodi, kuid üsna levinud strateegia, millest kirjutame üldisemalt funktsioonide pidevuse all [lk319] –idee on selles, et kui mõni reaalarvuline suurus muutub pidevalt, siis tema määramiseks piisab ainult ratsionaalarvuliste väärtuste teadmisest.
Selle argumendi võib aga siinjuhul kergesti ka üksipulgi kirja panna.
Sulle võivad huvi pakkuda need õppematerjalid:
Liitmine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonide graafikud
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 10 piires
Ruutvõrrand
8. klassi matemaatika teooriavideod
Lahutamine 20 piires
Liitmine 10 piires
Tasandilised kujundid
Ruutvõrrandi abil lahenduvad tekstülesanded
Kell ja kellaaeg
Kirjalik lahutamine
Ruutjuur, tehted ruutjuurtega
Funktsioonide graafikute lõikepunktide leidmine
xy-koordinaatsüsteem
Numbrilised seosed
Ratsionaalavaldised
Kirjalik liitmine
Liitmine ja lahutamine 20 piires
Hulknurkade pindalad
Ruut ja ristkülik
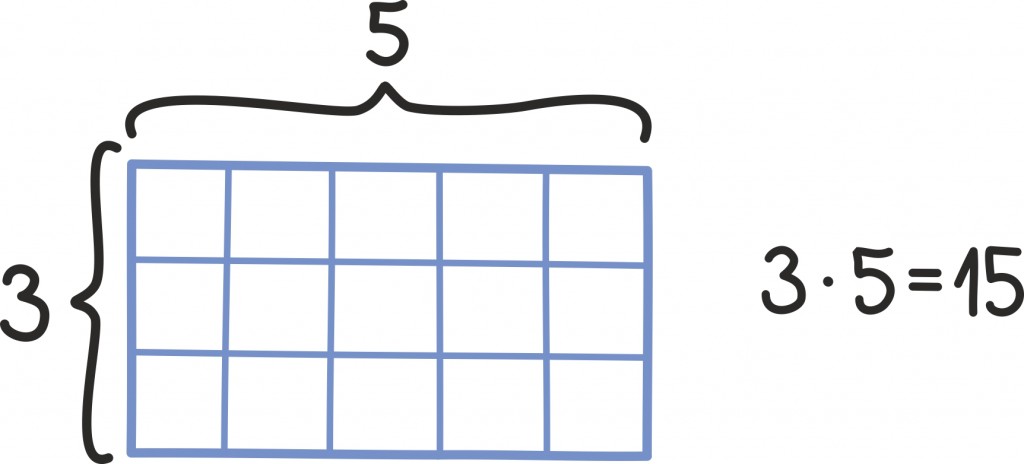
Mõtleme nüüd, kuidas oma ruudukujulise jupi abil välja nuputada ristküliku pindala. Kui küljepikkused on piisavalt sõbralikud, on see lihtne: näiteks jooniselt näeme, et külgedega 3 ja 5 ristküliku pindala on 3 · 5 = 15 ning külgedega 3⁄7 ja 1⁄2 ristküliku pindala on 3⁄14.
Ilmselt pole raske märgata, et näiteks kõik ratsionaalarvuliste küljepikkustega ristkülikud on sõbralikud: saame alati leida mingi imepisikese ruudu, mille abil ristkülik ruudukestega täielikult katta. Iga kord saame tulemuseks, et a · b ristküliku pindala on täpselt S = a · b.
Edasi peame taas kasutama ruudu küljepikkuse leidmisel mainitud „pidevuse printsiipi” – kui meil on mingi pidevalt muutuv reaalarvuline suurus, siis piisab sellest, kui me teame tema väärtusi ainult ratsionaalarvulistes kohtades. Nii võimegi väita, et iga a · b ristküliku pindala on
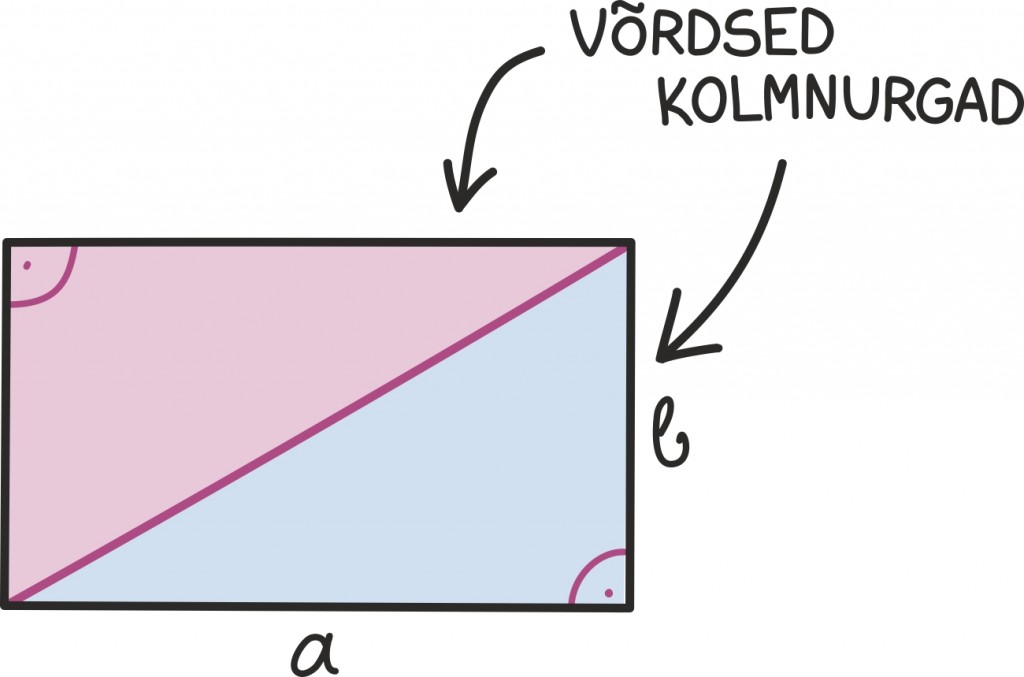
Kolmnurkadest on kõige lihtsam alustada täisnurksete kolmnurkadega – neid kaks tükki kokku pannes saame täpselt ristküliku:
Siit pole muidugi raske järeldada, et täisnurkse kolmnurga pindala on pool moodustunud ristküliku pindalast ehk
kus a ja b on tema kaatetite pikkus.
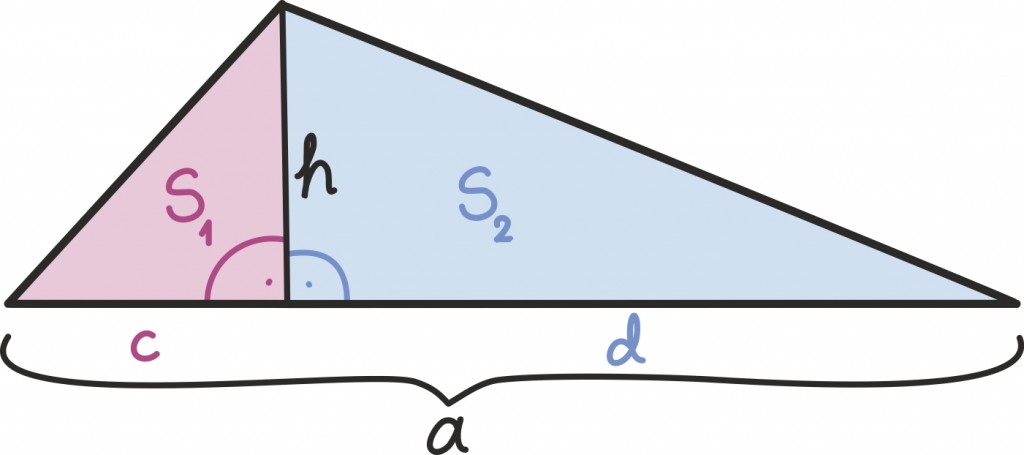
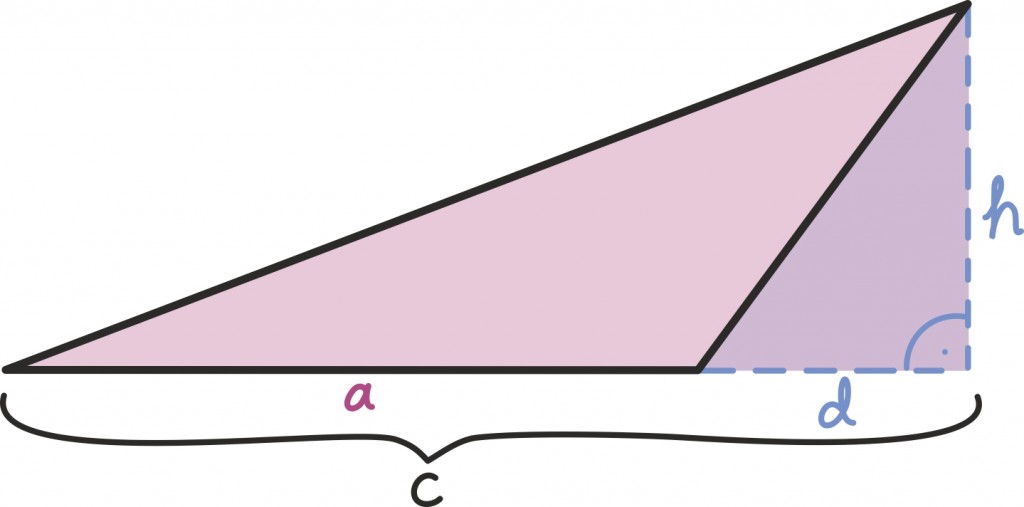
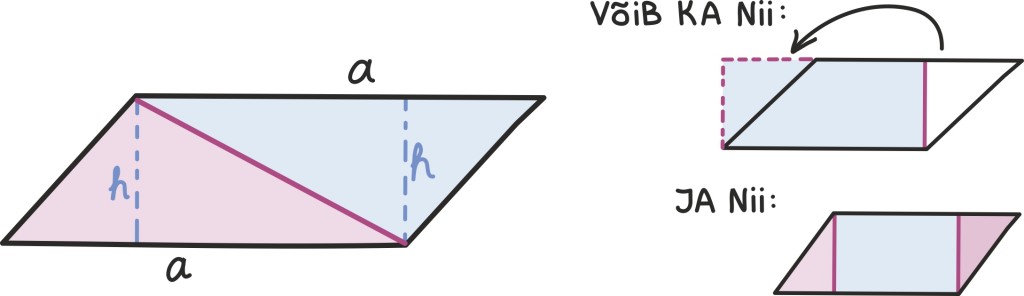
Aga nüüd võime ju etalonina juba kasutada ka täisnurkseid kolmnurki ja see teeb iga teise kolmnurga pindala leidmise väga lihtsaks: tõmbame lihtsalt kolmnurka mõne kõrguse ja jagame ta kaheks täisnurkseks kolmnurgaks!
Isegi kui joonised on erinevad, näeme, et järeldus on nii kolmnurga sisse kui kolmnurgast välja jääva kõrguse puhul sama – iga kolmnurga pindala on
kus a on mõni kolmnurga küljepikkus ja h tema vastastipust tõmmatud kõrguse pikkus.
Rööpkülik ja trapets
Rööpküliku võime jagada lihtsalt kaheks kolmnurgaks. Nii näeme, et rööpküliku pindala on S = a · h, kus a on tema vaadeldav küljepikkus ning h nende külgede vaheline kaugus. See tuleneb muidugi sellest, et mõlema kolmnurga pindala on eelmise osa põhjal
Nagu jooniselt näeme, võime rööpküliku pindala tuletada veel vähemalt kahel erineval moel:
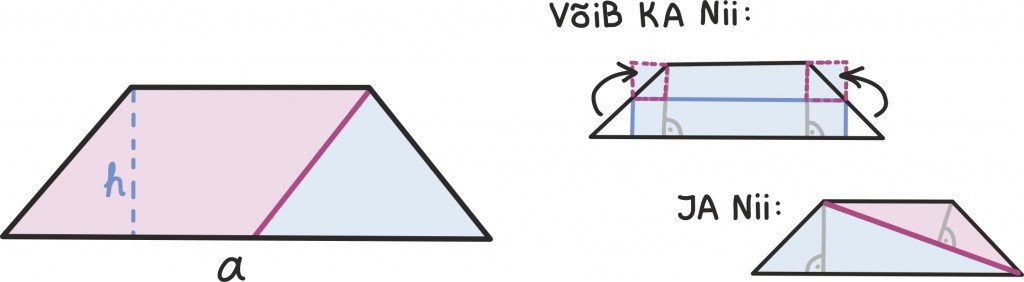
Ja trapets? Sama lugu, kasutame seniseid etalone, täisnurkseid kolmnurki ja ristkülikut, ning saamegi väikese kavaluse abil õpetaja väljakuulutatud tulemuse.
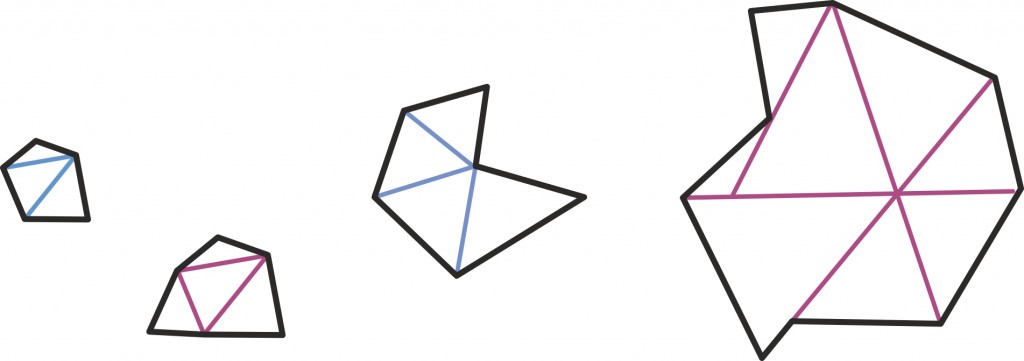
Tegelikult saame ju nüüd leida ka iga viisnurga, kuusnurga või ka kakssadanurga pindala, kui ainult kannatust jagub: võime nad ju alati jagada ühel või teisel viisil kolmnurkadeks (nii kuidas mugavam on) ja kolmnurkade pindalad kokku liita.
Ringi ümbermõõt ja pindala
Ring on oma olemuselt üks lihtsamaid ja ilusamaid kujundeid. Nagu nägime kuulsate arvude peatükis, võib teda ka mitmel moel defineerida ning temast mitmel moel mõelda [lk 96]. Siiski, hoolimata sellest, et ring on peale vaadates ilus ja lihtne kujund, peab temaga matemaatiliselt ümber käima teistmoodi ja isegi pisut keerulisemalt kui hulknurkadega.
Ringi ümbermõõduga pole asi siiski liiga hull. Kuna π on juba defineeritud kui ümbermõõdu ja diameetri suhe
siis ümbermõõdu P saabki sealt lihtsalt avaldada:
Traditsiooniliselt kirjutatakse see välja ringi raadiuse abil:
Kuidas aga leida ringi pindala?
Meie seniseid pindalade etalone on siin raskem ära kasutada – kõik nad olid nurgelised, samas kui ringjoon on ju kenasti kaardus. Seega peame olema kavalamad.
Üks võimalus on siiski kasutada juba teadaolevaid etalone, kuid seda koos integraaliga. Tuletame meelde, et integraali abil saame lähendada kujundite pindalasid, jagades kujundi õhukesteks ristkülikukujulisteks juppideks ning liites nad kokku. Piirprotsessis, kus õhukesi tükke on järjest enam, saamegi vastuseks täpse pindala. Sellest on meil natuke pikemalt juttu integraali peatükis [lk 347].
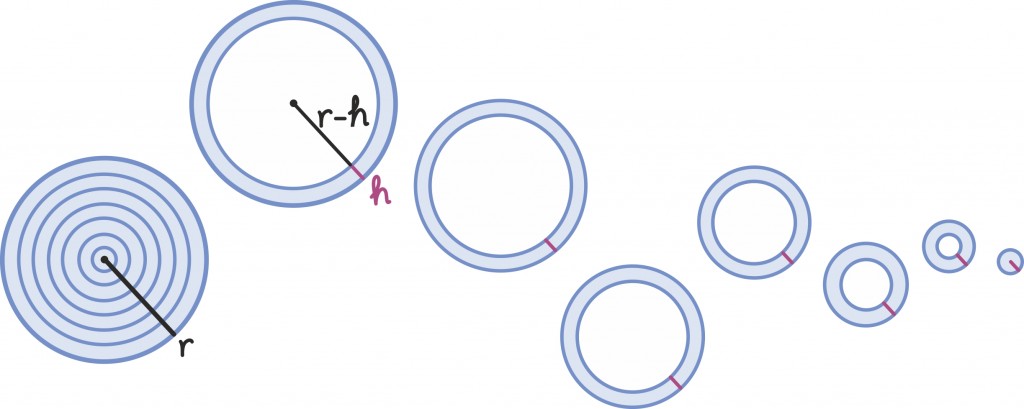
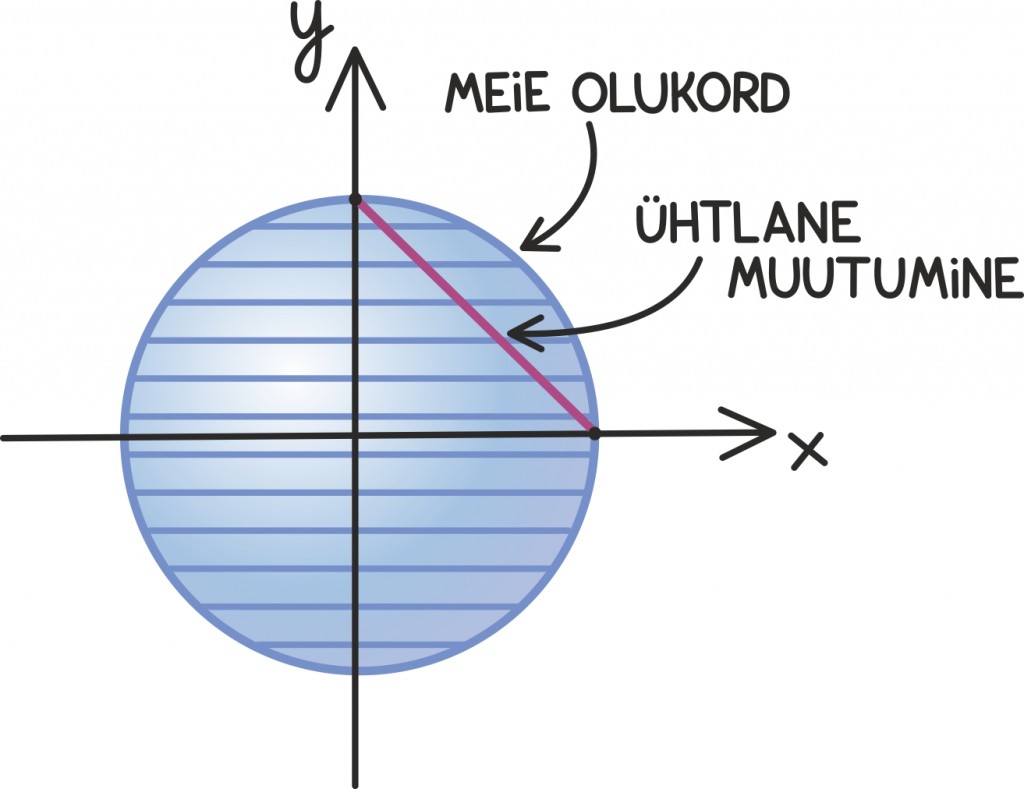
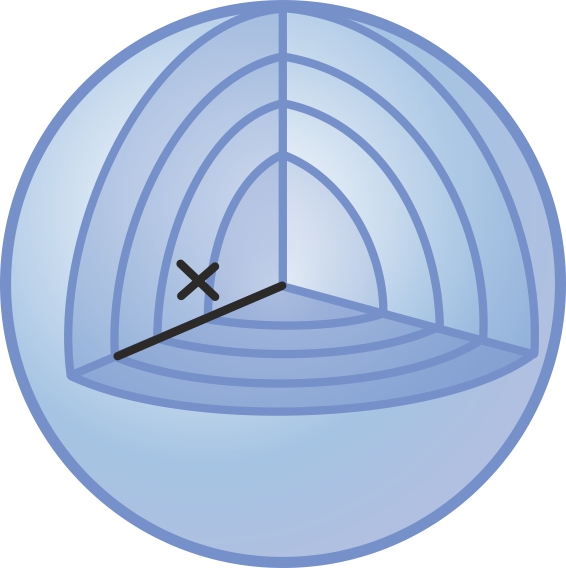
Siin kasutame vägagi sarnast ideed, ainult loobume kujundi ristkülikuteks jagamisest ning jagame ta hoopis väga paljudeks peenikesteks rõngasteks paksusega h, mis on õige sarnased juba ringidele. Nende raadiused muutuvad siis 0-ist kuni r-ini sammuga h.
Iga väike rõngas panustab algringi pindalasse umbkaudu 2πxh, kus x on näiteks rõnga välimise ringi raadius. Tõepoolest, kui paksus h on väga väike, siis ei pea rõnga sise- ja välisraadiust eristama. Pindala leidmiseks peame seejärel liitma kokku kõik need lõpmata paljud ümbermõõdud ja saame
Siin x1, … xn moodustavad aritmeetilise jada vahega h ja seega lähendavad lineaarfunktsiooni. Nüüd peaks meenuma, et see on juba väga sarnane meie määratud integraali kirjeldusele. Tõepoolest, piirprotsessis, kus ketaste paksus h→0, võimegi pindala kirja panna määratud integraali abil [lk 340]:
Edasi jääb vaid integreerida ja leiamegi kuulsa ringi valemi:
Kui tahame lugu veel enam integraali ja tuletise raamistikus näha, võib mõelda, et ringi pindala muutumise kiiruse annab just tema ümbermõõt. See on üsna loomulik, kuna ringi raadiust õige pisut, h võrra suurendades, muutub ringi pindala umbes hP võrra. h oleks selles kontekstis seega „aja parameetriks” ning kiiruse annakski ümbermõõt P.
Ruumiliste kujundite pindalad
Lisaks kahemõõtmelistele kujunditele võib meid muidugi huvitada ka mõne kolmemõõtmelise kujundi välispinna suurus.
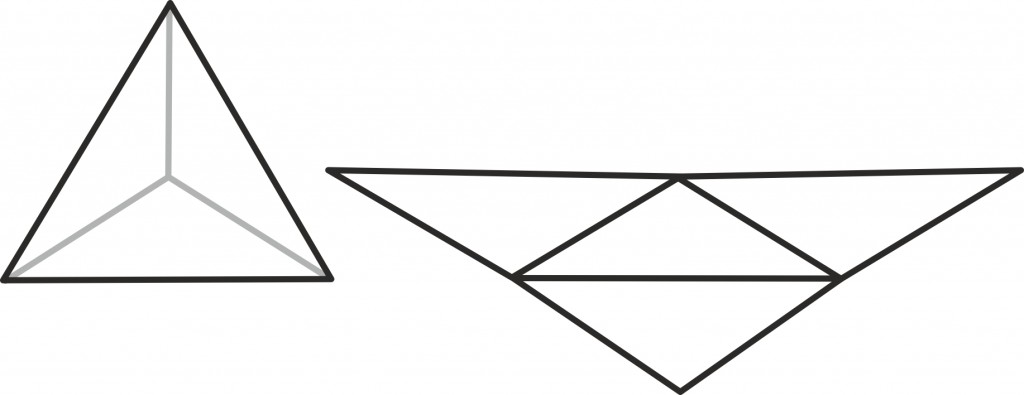
Hulktahukate ehk igasugu erinevate risttahukate ja püramiididega, mille tahud on hulknurksed, käib asi üsna lihtsalt: lõikame kujundi mööda servasid lahti ning arvutame iga tahu pindala eraldi välja. Liites need kõik kokku, saamegi kogu pindala.
Näiteks kolmnurkse põhjaga püramiidi külgpindala leidmiseks peame kokku liitma nelja kolmnurga pindala.
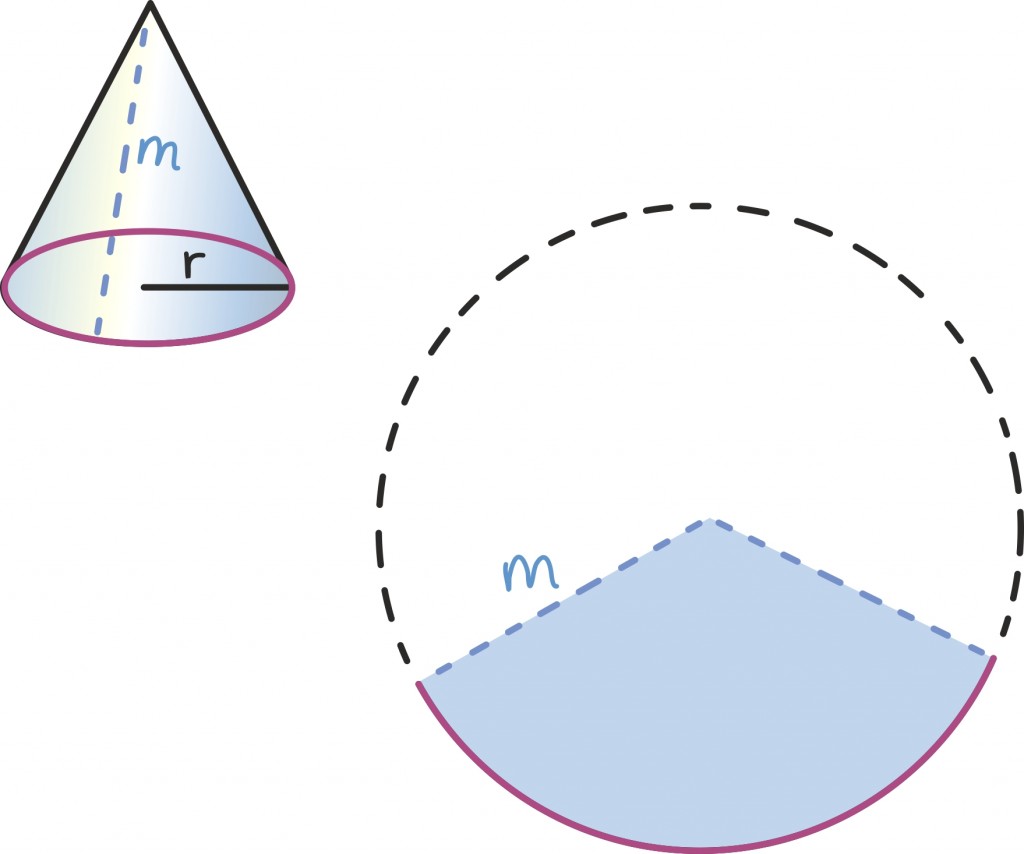
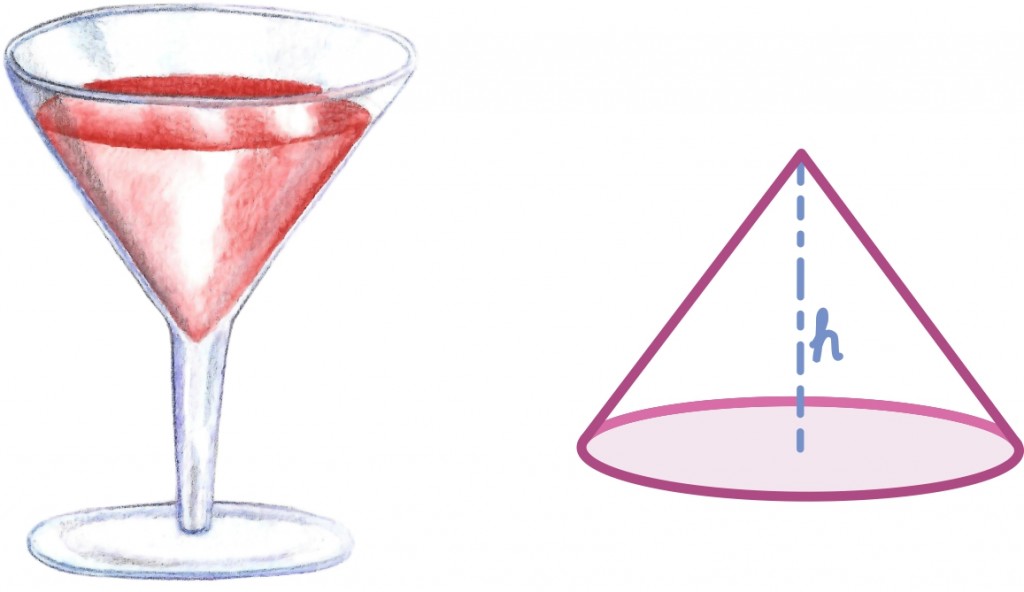
Koonuse pindala
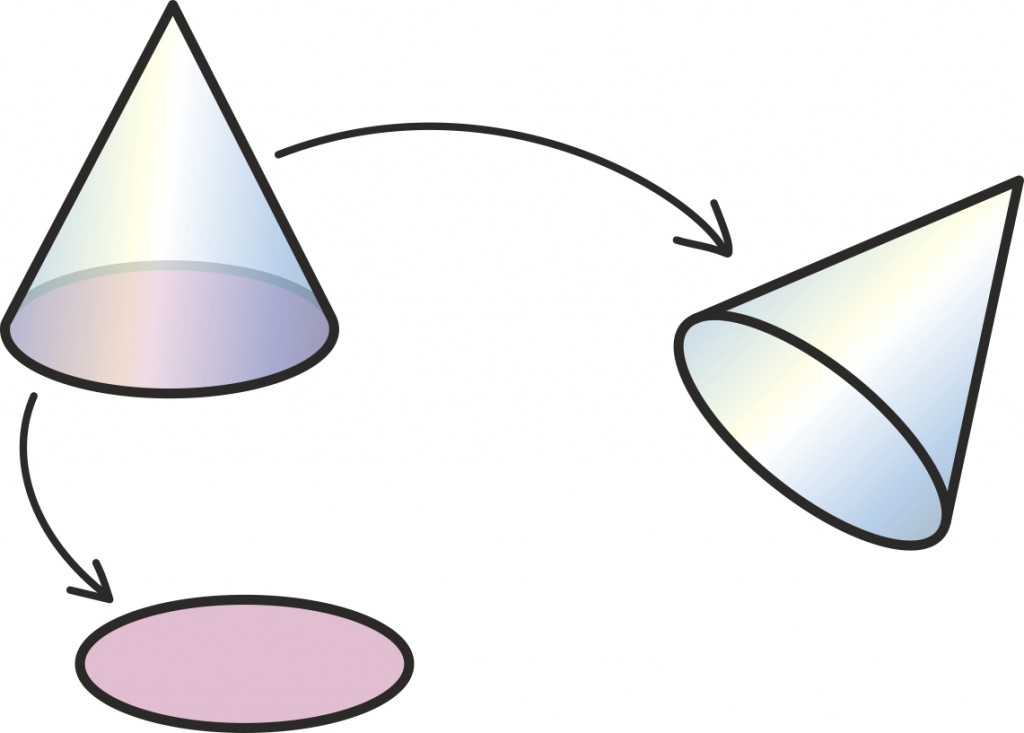
Üldiselt läheb kumeramate kehadega olukord keerulisemaks, aga koonuse korral aitab siiski üsna sarnane strateegia. Alustuseks võime koonuse pinna jagada kaheks – saame ringikujulise põhja ning teatava kujuga külgpinna.
Kuna ringi pindala juba oskame leida, on põhja pindala arvutamine kerge. Aga kuidas leida selle allesjäänud koonuselise tüki pindala?
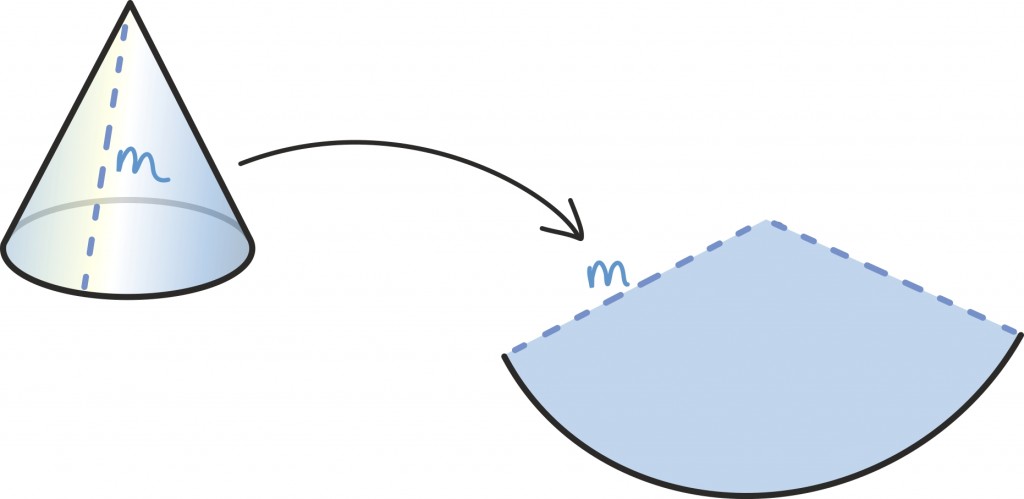
Seegi kord aitab meid veel lõikamine ning tasandile asetamine. Nimelt kui lõikame koonuse külgpinna mööda moodustajat – ehk mööda suvalist koonuse tippu ja põhja äärt ühendavat sirglõiku – lahti ja laotame tasandile, saame ilusa ringi sektori.
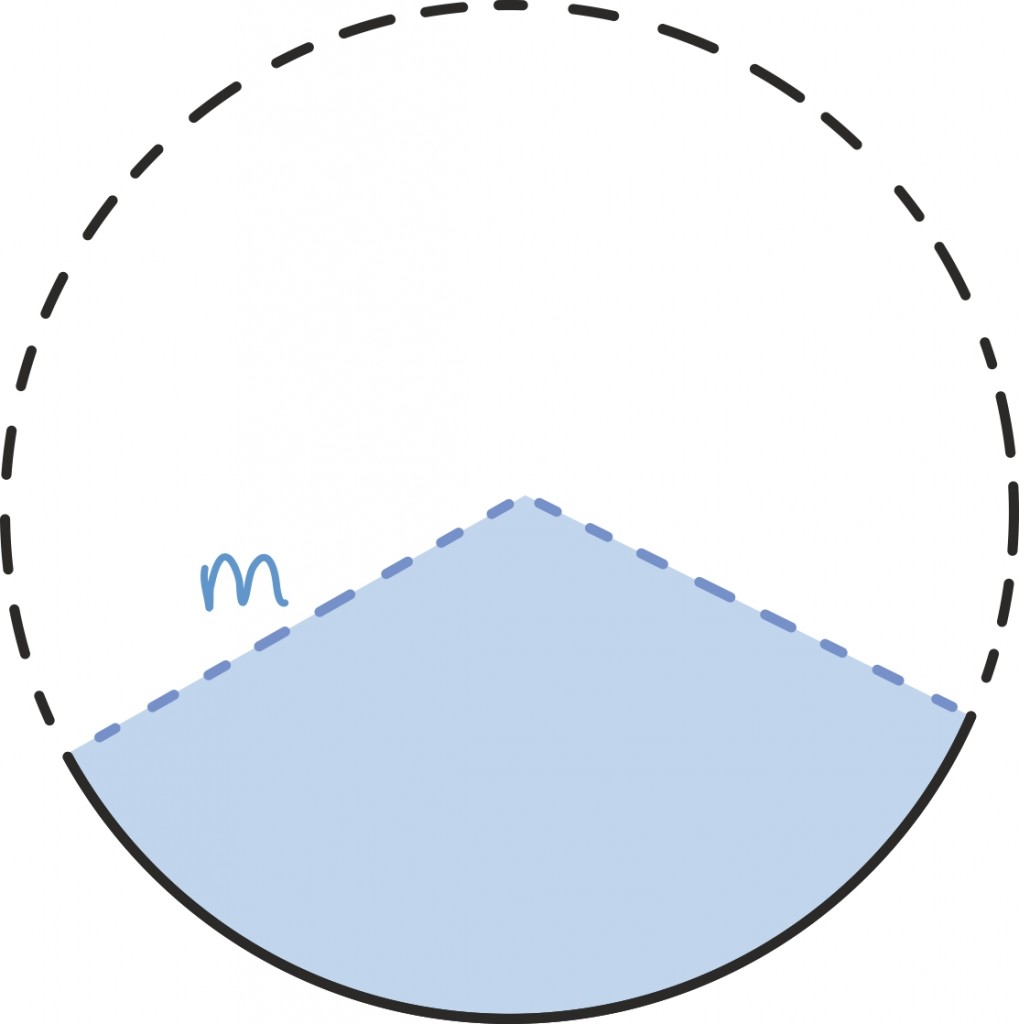
See sektor moodustab teatava osa suurest ringist raadiusega m, kus m on siis niinimetatud koonuse moodustaja. Selle algse ringi pindala oskame jälle lihtsalt leida:
Seega oleks vaja lihtsalt aru saada, kui suure osa moodustab laiali laotatud sektor kogu ringist. Ringjoone sektori pindala suhe kogu ringi pindalasse on aga täpselt sama kui sektori kaarepikkuse suhe kogu ringjoone ümbermõõtu. Kuna kogu ringi ümbermõõt on meile teada (2mπ), siis piisab lihtsalt sektori kaare pikkusest. Sektori kaare pikkus on aga täpselt koonuse põhja ümbermõõt! Seega, kui põhja raadiuseks on näiteks r, siis saame põhja ümbermõõduks ja ka kaare pikkuseks 2rπ.
Kui jagame saadud tulemused, näeme, et sektori pindala moodustab kogu pindalast
Nüüd võime külgpindala leida, korrutades saadud suhte läbi suure ringi pindalaga:
Liites põhja pindala:
Võime leida ka koonuse täispindala
Kera pindala
Kera pindala leidmiseks aga mõnest lõikamisest enam tõesti ei piisa. Võite proovida apelsinikoort mõistlikult laua peale laiali laotada, nii et ükski koht õhus ei oleks – lihtne see ei ole. Tuleb kasutada juba ringi pindalast tuttavat integreerimise strateegiat.
Intuitiivselt tahaksime ka seekord pinna rõngasteks jagada ning seejärel nende rõngaste pindalad osavalt kokku liita.
Ringi pindala leidmisest on olukord pisut keerulisem, kuna rõngaste pindalad ise ei muutu enam ilusalt ühtlaselt.
Seega piirdume siinkohal lihtsalt kera pindala valemiga:
Kera ruumala juures anname siiski ka ühe viisi selle pindala leidmiseks.
Mõned ruumalad
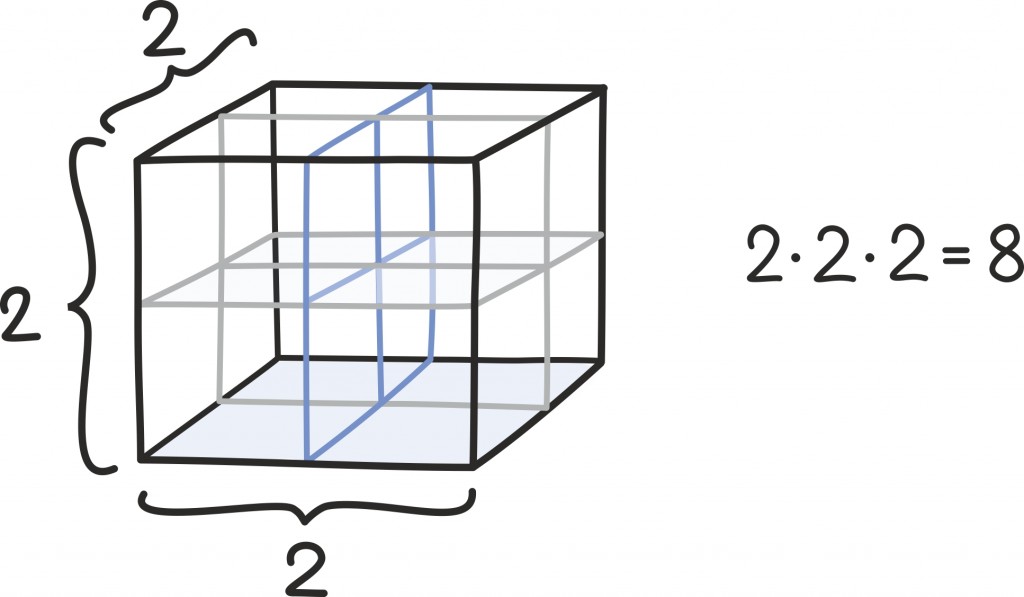
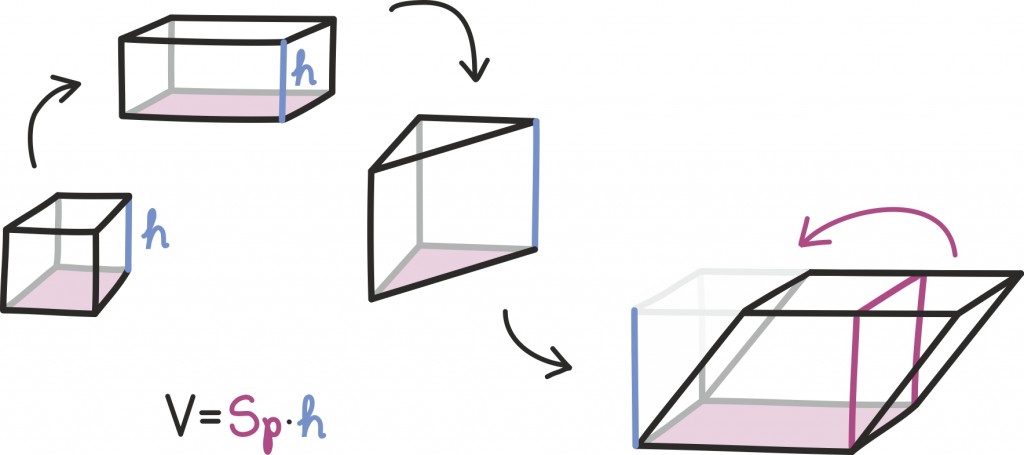
Laias plaanis võime ruumalade leidmisel käituda üsna analoogiliselt pindalade juhule: alustame kuubi ruumalast, siis leiame risttahuka ruumala, seejärel rööptahuka ruumala ja nii edasi.
Natuke keerulisemaks läheb püramiidide korral, aga siiski aitab natukene kavalust meid hädast välja.
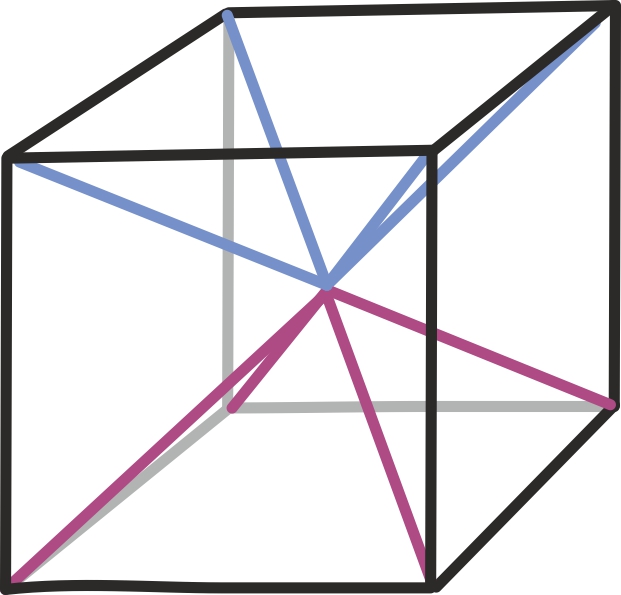
Näiteks toodud jooniselt näeme, kust tuleb vähemalt ruutpüramiidi korral kurikuulus üks kolmandik: nimelt saame täita ühikkuubi kuue võrdse ruumalaga püramiidiga, mille kõrgus on täpselt pool kuubi küljest.
Kõikide võimalike eripüramiidide jaoks samasuguste konstruktsioonide väljanuputamine osutub juba aeganõudvaks, kuigi on ilmselt võimalik nii kaua, kuni aluspinnaks on mõni hulknurk. Jällegi on idee alustada lihtsamatest püramiiditüüpidest ning samm-sammult minna üldise kuju poole – see osutub üsna pikaldaseks, kuna peame sisuliselt iga püramiidi külge ükshaaval lihtsamast keerulisemaks muutma.
Võib siiski kinnitada, et püramiidi ruumala valem jääb samaks:
kus Spõhi on seekord püramiidi aluse pindala ning h tema vastastipust tõmmatud kõrgus. Seesama valem jääb kehtima ka siis, kui aluseks on hoopis ring.
Toodud valemi sarnasus kolmnurga pindala valemiga võib mõtlema panna, kas neil kahel on mingi seos – räägime mõlemal korral ju alusest ja kõrgusest ning eesolev kordaja paistab täpselt seoses olevat ruumimõõtmete arvuga. See seos põhineb tegelikult väga lihtsal mõttel, mida juba ka mainisime.
Nimelt nägime ringi pindala juures, et ringi raadiust suurendades võime mõelda, et ringi pindala kirjeldava funktsiooni tuletiseks on tema ümbermõõt.
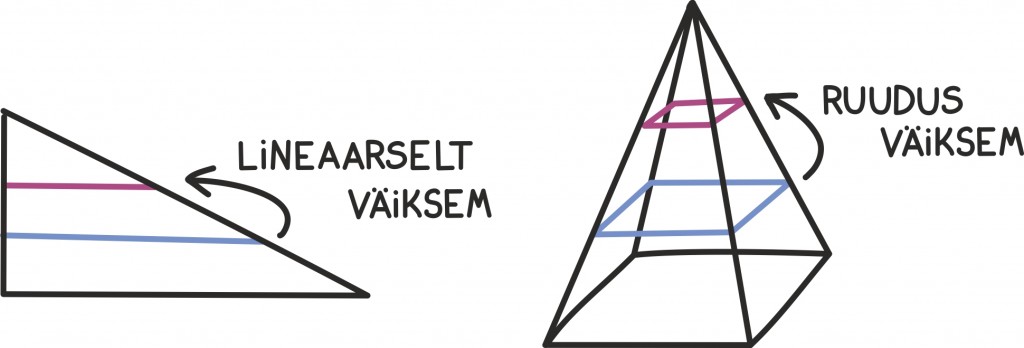
Samamoodi võime mõelda, et mõõtes kolmnurga kõrgust, on kolmnurga pindala muutumise kiiruseks tema alumise külje pikkus. Kui aga leiame püramiidi ruumala kõrgusest sõltuvalt, on muutumise kiiruseks hoopis tema põhja pindala:
Nüüd on lihtne veenduda, et kolmnurga aluse pikkus sõltub tema kõrgusest lineaarselt – ehk seda võib kirjeldada funktsiooni abil. Püramiidi pindala aga muutub kõrguse suhtes nagu ruutfunktsioon ax. Esimese integreerimisel saame ette kordaja 1⁄2, sest kui seame integreerimisega kaasaskäiva konstandi nulliks, saame
ning teise integreerimisel leiamegi kordaja 1⁄3?:
Täpsemat näidet esimesest viisist nägime ringi pindala leidmisel, teise näite teeme läbi nüüd kera ruumala arvutamiseks.
Kera ruumala
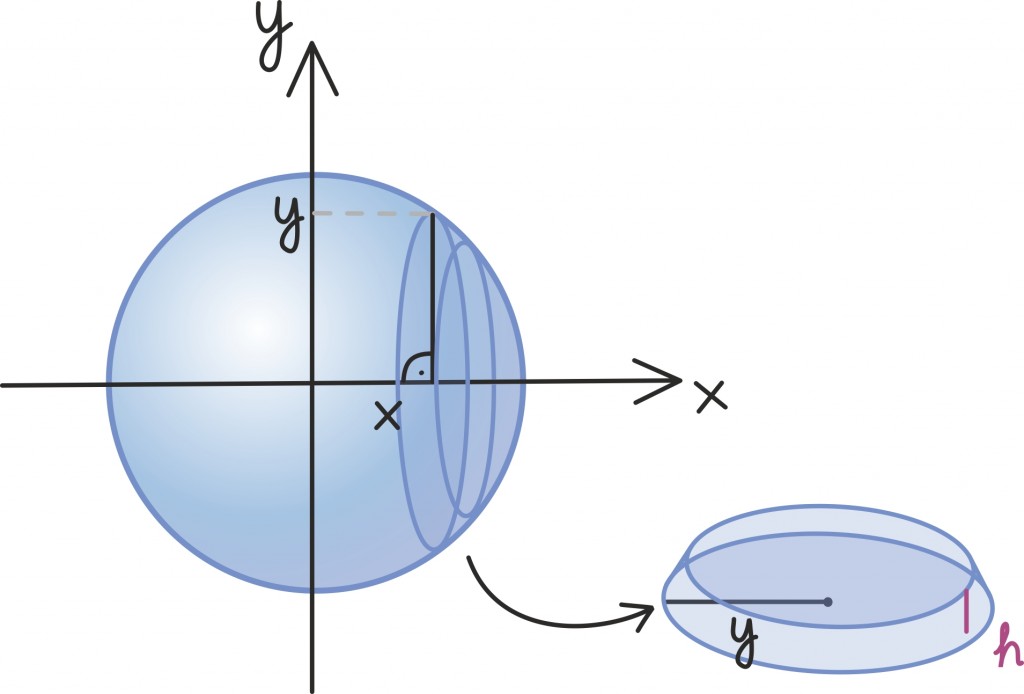
Kera ruumala on jällegi raske leida lihtsalt nurklike etalonide abil. Peame kasutama ringi pindala puhul abiks olnud strateegiat – integreerimist. Teisisõnu lähendame kera paljude õhukeste ketastega, leiame nende ruumalad ning liidame nad kokku. Piirprotsessis saame integraali, mis annabki meile koguruumala [lk 347].
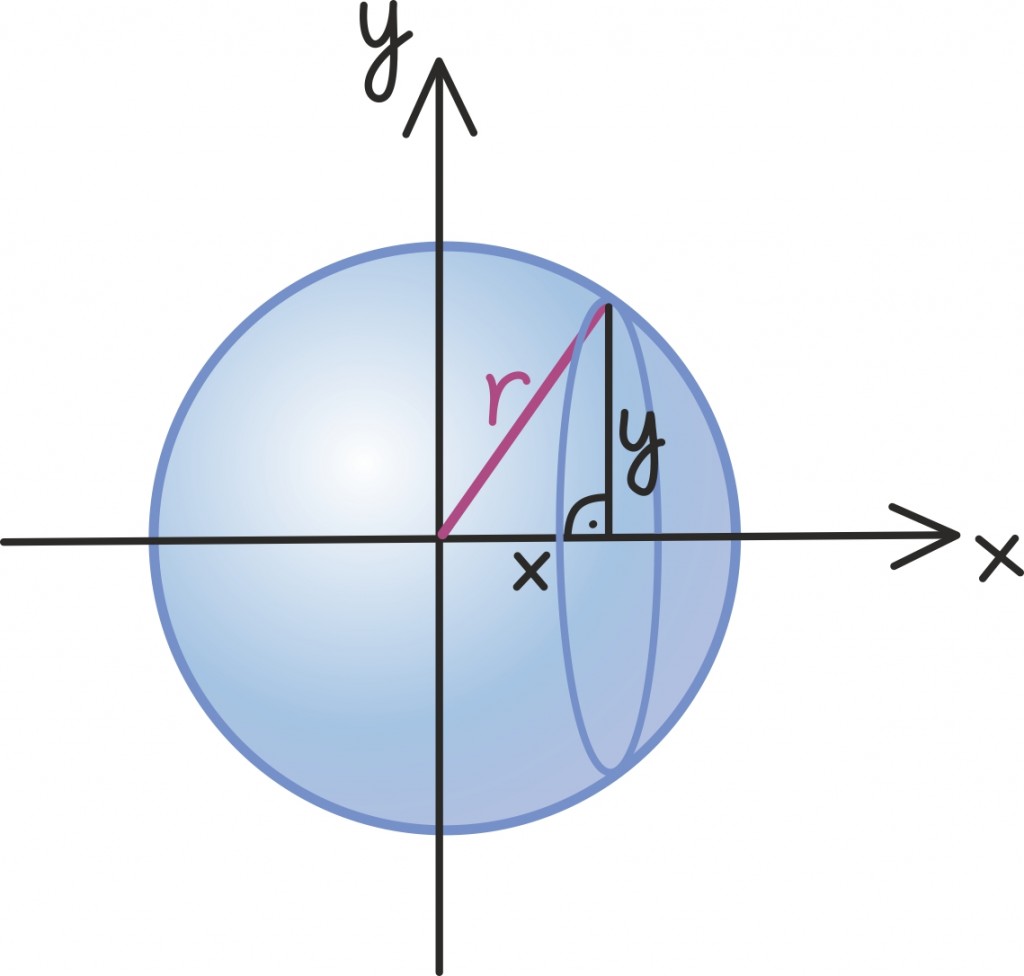
Tähistame tähega x horisontaalset kaugust kera keskpunktist ning tähega y kera pinnal asuva ringjoone raadiust tollel kaugusel. Ketta, mille välimine äär on kaugusel x ning mille paksus on h, ruumala on umbkaudu h · πy2 ehk πhy2.
Selle ringjoone raadiuse y, mis sõltub x-ist ja kera raadiusest r, saame avaldada Pythagorase teoreemi kaudu: y2 = r2 – x2.
Neid kettaid aina väiksema paksuse korral kokku liites saame nagu kera pindala leidmiselgi integraali [lk 340], seejuures vasemalt äärelt paremale välja jõudmiseks muutub horisontaalne kaugus x vahemikus [–r, r]. Seega võime ruumala kirjutada järgmise integraalina:
Seda oskame kooliõpiku abil juba arvutada:
Tulemuseks saamegi kera ruumala valemi
Huvitav on see, et sellest kera ruumala valemist saame tegelikult nüüd tuletada ka kera pindala valemi. Nimelt võiksime ju ka mõelda, et kera koosneb mitte ketastest, vaid hoopis sfäärilistest kihtidest:
Seega saaksime kera ruumala, kui liidaksime kokku nende sfääriliste kihtide ruumalad. Keskpunktist kaugusel x asuva peenikese sfäärilise kihi ruumala oleks nüüd umbes Sxh, kus Sx on raadiusega x kera pindala ning h siis õhukese sfääri paksus. Seega võiksime analoogiliselt eelnevaga kirjutada ruumala integraalina üle nende sfääriliste kihtide:
See aga tähendab täpselt, et kui vaatame kera ruumala kui funktsiooni raadiusest, siis on kera pindala selle funktsiooni tuletis! Seega kui teame juba kera ruumala, võime leida tema pindala, kasutades integraali ja tuletise vahelist seost.
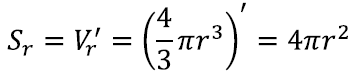
Kochi lumehelves
Muidugi tahaksime, et matemaatikas oleks kõik nii, nagu meie vaist seda õigeks peab. Siiski selgub, et niipea kui mõne definitsiooni rangelt matemaatiliselt kirja paneme, alustab ta justkui oma elu, libiseb meie käe alt välja ja korraldab midagi üllatavat. Tihti peame seejärel matemaatikaga paremaks läbisaamiseks oma intuitsiooni ümber kujundama.
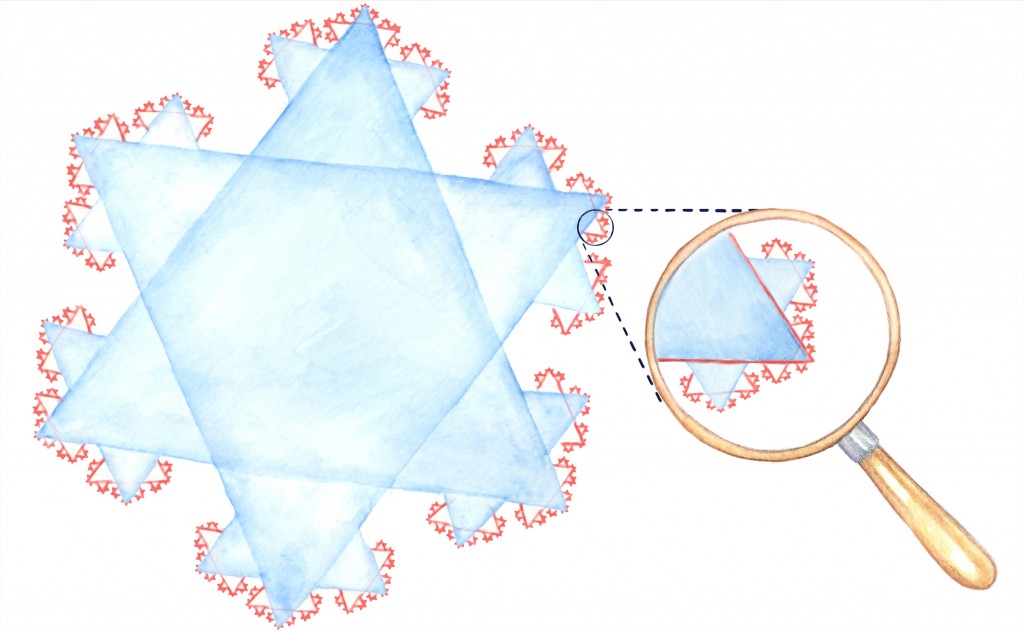
Kirjeldame järgnevalt ühte kujundit, mis näibki algul pigem mõistusevastane: tal on lõplik pindala, aga lõputu ümbermõõt. Seda kujundit kutsutakse Kochi lumehelbeks.
Kochi lumehelbe saamiseks peame läbima järgmise protsessi:
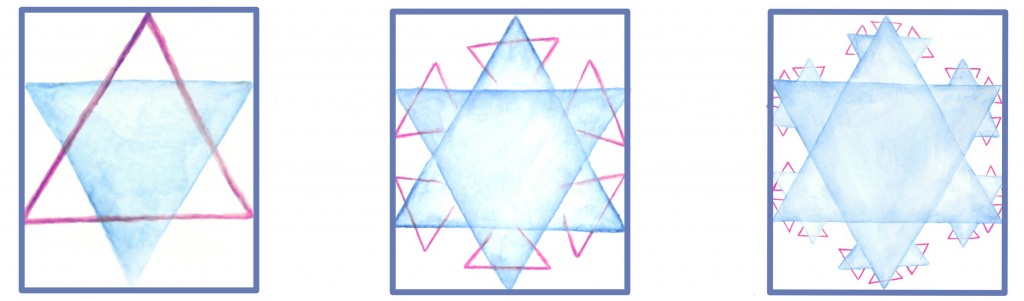
- alustame võrdkülgsest kolmnurgast,
- esimesel sammul jaotame iga külje kolmeks võrdseks osaks ja ehitame iga külje keskmisele kolmandikule väljapoole võrdkülgse kolmnurga, nagu jooniselt näha, võib nüüd eristada kuut väiksemat kolmnurka, millest igal on kaks väljapoole avatud külge,
- edasi konstrueerime analoogselt eelnevaga iga väljapoole avatud külje keskele uuekolmnurga,
- Aina jätkame ja jätkame protsessi uute, väiksemate külgedega…
Nagu jooniselt näeme, tekib nii midagi lumehelbe sarnast. Kui protsessi kangekaelselt jätkata, näeb tekkiva kujundi piirjoon iga suurusega luubi all välja umbes ühesugune (alati paistab, et on üks külg, mille keskele on konstrueeritud kolmnurk, ja siis veel natukene väikest müra):
Mis võiks olla tekkiva kujundi ümbermõõt? Kui alguses on kolmnurga ühe külje pikkus 1, siis pärast esimest etappi oleme külje asendanud 4 lõiguga, millest igaühe pikkus on 1⁄3 ehk kokku on tema pikkus 4⁄3. Igal järgmisel etapil on 4 korda rohkem lõike, kuid iga lõik on 3 korda lühem ehk lõikude kogupikkus suureneb 4⁄3 korda.
Seega pärast sajandat konstruktsiooni on lõikude kogupikkus juba
ning protsessi lõpmatult jätkates muutub ka kujundi ümbermõõt lõpmata suureks:
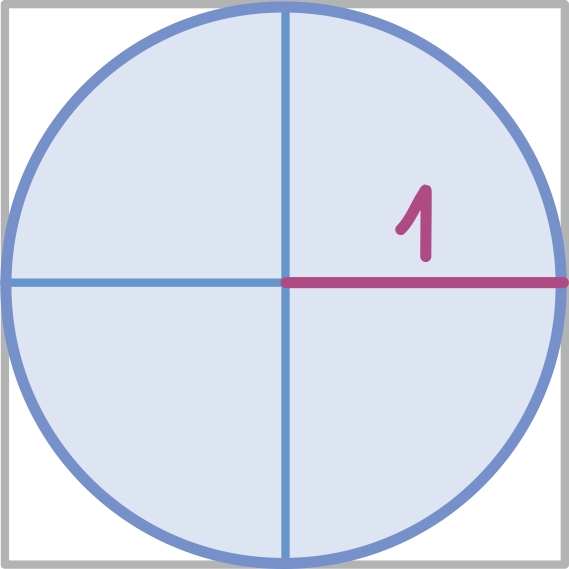
Lähemalt vaadeldes selgub samas, et pindala ei saa sellel kujundil väga suur olla ja kindlasti peab ta olema lõplik. Nimelt mahub Kochi lumehelves näiteks alati joonisel toodud sinisesse ristkülikusse:
Pärast mõningat arvutustööd selguks, et tema pindala on täpselt
Kui nüüd järele mõtleme, miks meile toodud olukord paradoksaalne tundub, siis ilmselt on põhjus väga lihtne: igapäevaelus me ilmselt sellist kujundit kohanud pole, kus ümbermõõt oleks lõpmatu ning pindala lõplik. Meie masinavärk ei luba lihtsalt selliseid pikkuseid mõõta: päriselus ei ole meil tegelikult ju kasutada lõpmatu suurendusega luupe ning iga lõpliku suurusega luubi korral tunduks ka Kochi lumehelbe ümbermõõt lõplik. Samuti paistab, et tänane füüsika ei tahaks hästi selliseid kujundeid lubada.
Siiski, matemaatikat need kaalutlused ja kitsendused ei sega – võime sama vabalt leida ka näiteks lõpmatu pindala ja lõpliku ruumalaga kujundeid (näiteks niinimetatud Gabrieli pasun) ning teisi sarnaseid veidrikke.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!