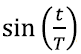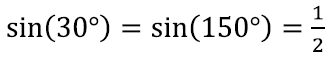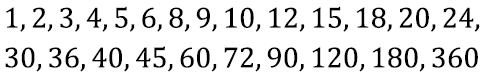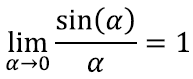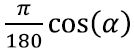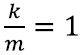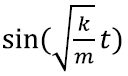Trigonomeetria ja perioodilised funktsioonid
Eelmises peatükis jõudsime trigonomeetriliste funktsioonideni, uurides küljepikkuste suhteid täisnurkses kolmnurgas. Saadud funktsioone kasutasime edasi seoste leidmiseks suvalise kolmnurga küljepikkuste ning nurkade vahel.Tänu neile seostele muutus kolmnurga puuduvate elementide kindlaks tegemine hoobilt üsna lihtsaks.
Siinus ja koosinus tulevad funktsioonidena aga esile veel teiseski kontekstis – looduse perioodiliste ehk korduvate protsesside kirjeldamisel.
Seda võib igaüks (juhul kui koristamine vastumeelt ei ole) ka kodus proovida. Seo pika nööri otsa üks korralik pang, kalla värvi täis ning tee põhja sisse auk. Lisaks varu suur rull paberit.
Nüüd pane see pang pendlina võnkuma ning tõmba paberit ühtlase kiirusega pange alt läbi. Paberile tekkiv värvijoon ongi ilus siinuse või koosinuse graafik.
Skeptiline lugeja võib muidugi kahelda, miks peaks paberile joonistuma täpselt siinus või koosinusfunktsioon ja mitte mõni teine sarnase kujuga perioodiline funktsioon.
See kahtlus on igati õigustatud – on ju nii palju erinevaid perioodilisi funktsioone, miks peaks loodus just trigonomeetriliste funktsioonide otsa komistama? Ometigi komistab. Selle põhjendamine on aga juba pisut keerulisem ning nõuab ka parasjagu füüsikat – huvitunu ja skeptik saab sellest lugeda lisapeatükist [lk 236].
Järgnevalt üritame aga intuitiivselt aru saada, kuidas perioodilised liikumised trigonomeetriaga seotud on, ja teeme seda kõige kaunima perioodilise liikumise, ringliikumise näitel.
Ringliikumine ja trigonomeetria
Lähed sõitma 100-meetrise diameetriga vaaterattaga. Kas oled mõelnud, kuidas muutub vaaterattaga sõidu ajal Sinu kõrgus maapinnast? Võibolla Su kaaslane kardab kõrgust, võibolla armastab. Oskad talle öelda, kui palju aega veedate äärmustes – hästi kõrgel või hästi madalal – ning kui palju ülesminekul ja allatulekul?
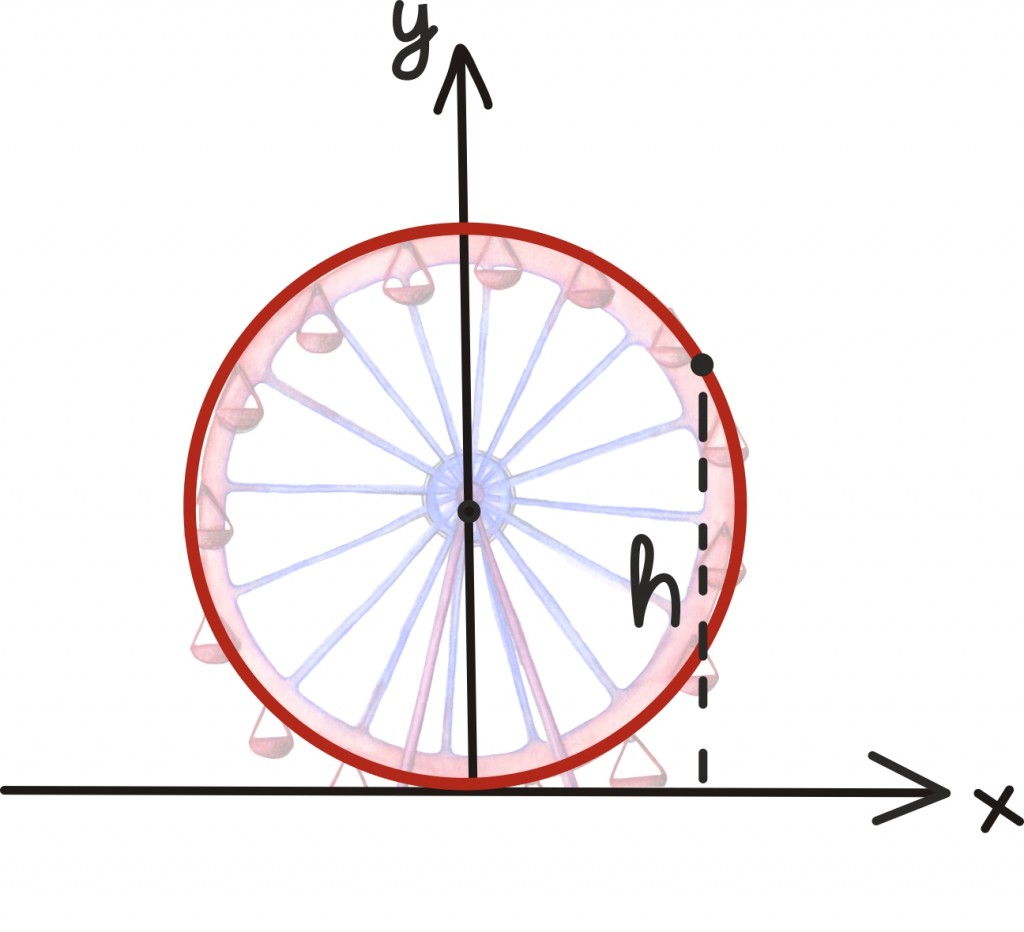
Neile küsimustele saab matemaatiliselt kenasti vastata. Matemaatiliseks lähenemiseks peame kõigepealt nii mõnedki detailid ära unustama: näiteks selle, kui ilus on vaade, kui kaunis kaaslane või kui logu on vaateratas ise. Järele jääb pöörlev ringjoon koos punktikesega, millele võime mõõtmiseks taustale lüüa ka koordinaattasandi nii, et x-teljeks on maapind.
On üsna mõistlik oletada, et vaateratas liigub ühtlase kiirusega – muidu saaks ju mõnes kabiinis istujad ägedamat sõitu kui teised.
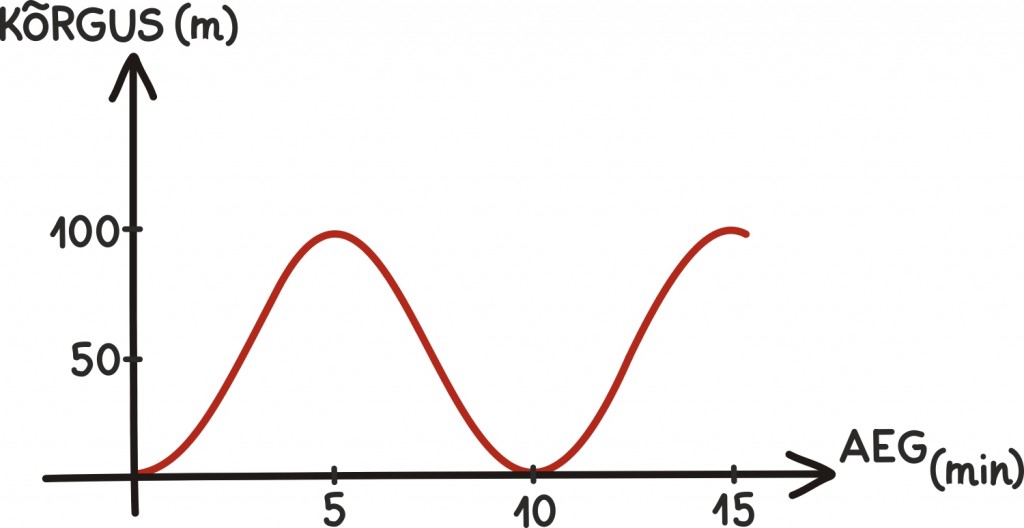
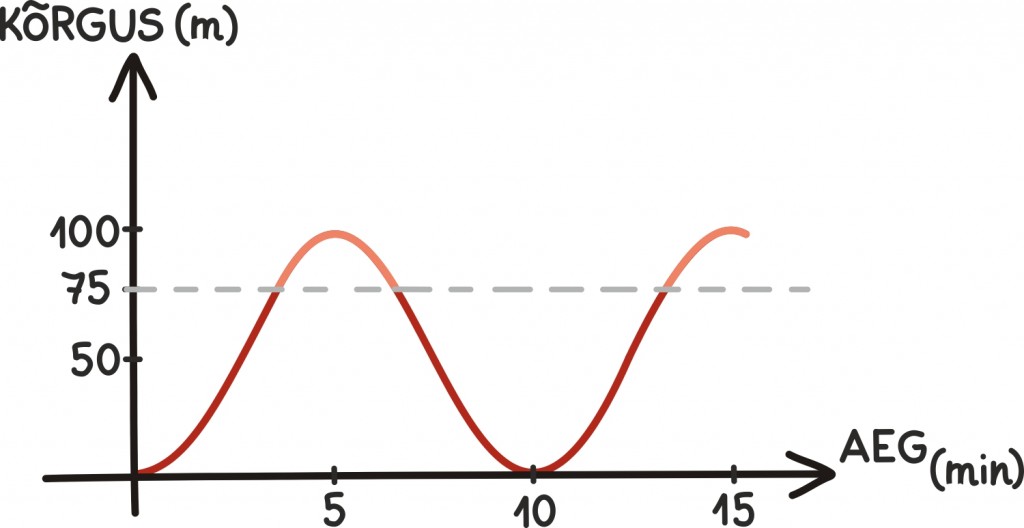
Kõrgus on nüüd vastavuses teljestiku y-koordinaadiga. Kui oletame lisaks, et täispöörde läbime 10 minuti jooksul, võime joonistada ka oma kõrguse profiili. Peale ronid vaaterattale muidugi päris alt.
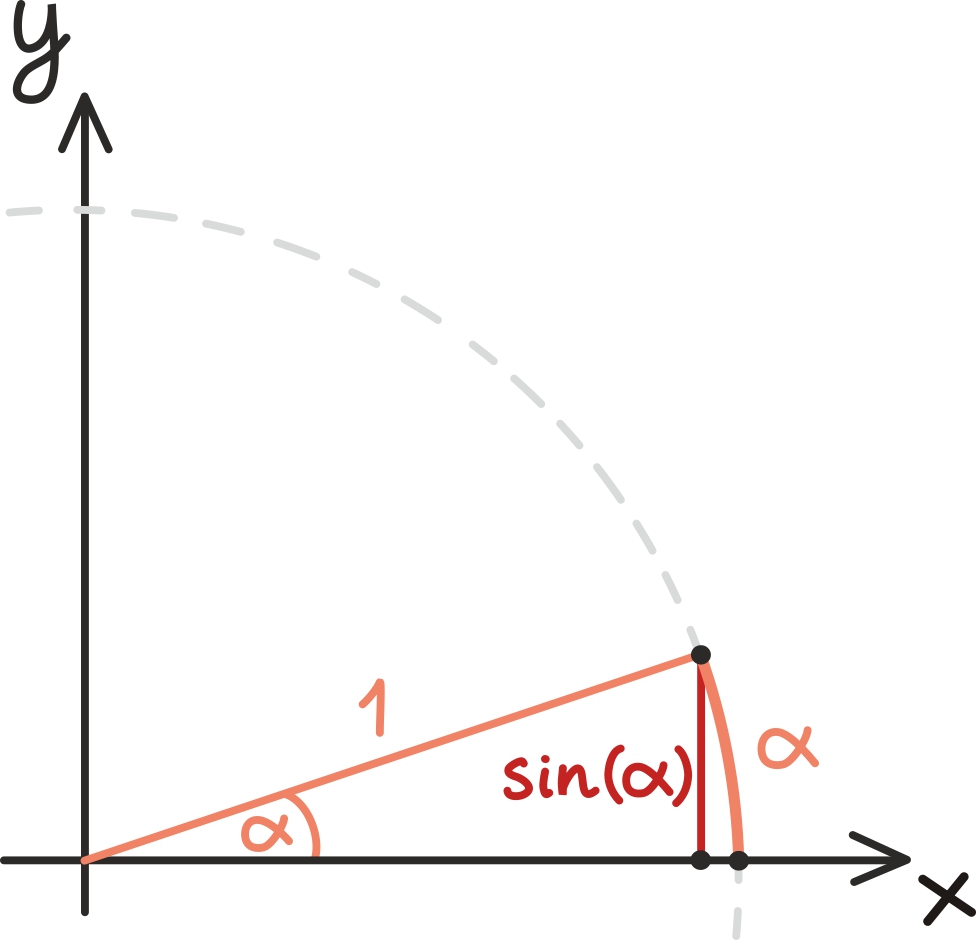
See näeb ju aga välja täpselt nagu siinusfunktsioon, ainult pisut ülespoole nihutatult ning pisut suurendatult. Ja tõepoolest, tuletades meelde, kuidas me eelmises peatükis siinusfunktsiooni defineerisime, ei tohiks see üllatada.
Defineerisime ju nurga siinuse täpselt kui nurga haara ja ühikringjoone lõikepunkti y-koordinaadi. Seega kui nüüd nurka ühtlaselt suurendada, saamegi ringliikumise ja seega kõrguskoordinaat joonistab siinusfunktsiooni. Muidugi, see funktsioon ei pruugi olla täpselt kujus sin(t), vaid võib olla kujus
kus T on aeg, mis kulub ühe täispöörde jaoks.
Nüüd võime ka vastata tekkinud küsimustele. Kui palju aega veedad vaaterattaga päris üleval, kõrguse ülemises neljandikus?
Graafikul huvitab siis meid, kui palju aega asub kõrgusfunktsioon oma maksimumi suhtes ülemises neljandikus:
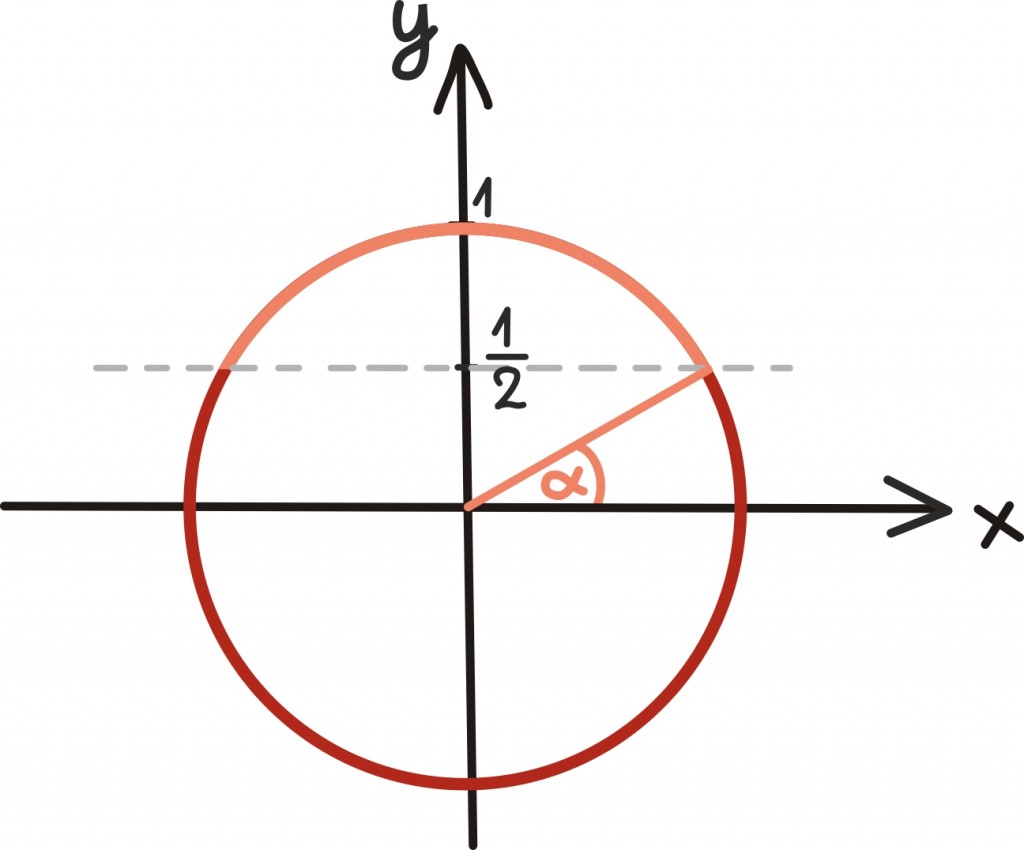
Kuna liikumine on ühtlane ja veedame ringjoone igas punktis sama kaua aega, võime oma küsimuse ümber tõlgendada üsna lihtsaks geomeetriliseks küsimuseks: kui suur osa ühikringjoonest asub kõrgemal kui ½?
Seega on vaja lihtsalt leida, milliste x-i väärtuse korral on sin(α) ≥ ½. Õnneks näitab järgnev ilus geomeetriline konstruktsioon täpselt, et
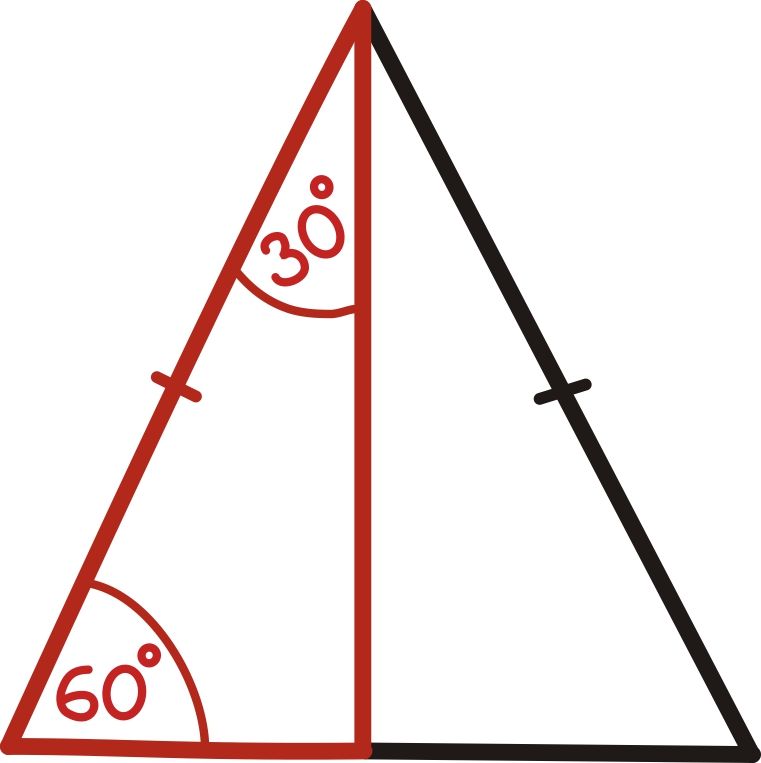
Joonistame 60º-30º kraadi kolmnurgale juurde teise samasuguse. Kuna tekkinud kolmnurk on võrdkülgne, siis tema servad on võrdsed. Järelikult sin(30º) on pool külge jagatud terve küljega ehk 0,5.
Kuna 150 – 30 = 120 kraadile vastav ringjoone osa on täpselt kolmandik kogu ringjoonest, võimegi öelda, et ülemises neljandikus veedate kolmandiku koguajast. Päris hea tehing!
Meelde jätta võiks sellest peatükist aga hoopis seda, et trigonomeetrilistele funktsioonidele võibki läheneda ka hoopis ringliikumise vaatevinklist!
Sulle võivad huvi pakkuda need õppematerjalid:
Kirjalik liitmine
Ruutjuur, tehted ruutjuurtega
8. klassi matemaatika teooriavideod
Üksliikmed, hulkliikmed ja tehted nendega
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine eelkoolile
Harjutusülesandeid matemaatika riigieksamiks
Funktsioonid ja nende graafikud
Ruutvõrrand
Hariliku murru kordamine
Tasandilised kujundid
Liitmine 10 piires
Numbrilised seosed
Kell ja kellaaeg
II kooliastme matemaatika reeglite kordamine
Geomeetria
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Liitmine ja lahutamine 10 piires
Funktsioonide graafikud
Algebralised murrud
Kraadid ja radiaanid
Seni oleme hoidunud arutelust, kuidas nurka peaks mõõtma – kas seda oleks targem teha kraadides või radiaanides? Õigupoolest oleme seda seni teinud ainult kraadides. Ometigi on nii mõnigi kord kasulikum kasutada hoopis radiaane.
Juba kraadidest ja radiaanidest mõtlemine on üsna erinev.
Kraadid
Kraadides mõõtmine on nurga tipus istujale. Kraadide leidmiseks vaatame lihtsalt, kui suure osa täispöördest moodustab nurk kahe nurgahaara vahel.
Kraadides arvestatakse näiteks tihti kaugete objektide mõõte ja vahemaid.
Kraadide juurde käib ka üks huvitav kokkulepe. Nimelt tundub, et kuskil ajaloohämaras on mingi hetk üsna vägivaldselt otsustatud, et täispööre olgu täpselt 360 kraadi. Muud nurgad arvestatakse siis vastavalt sellele, kui suure osa täispöördest nurk moodustab – näiteks pool pöördest on siis täpselt 180 kraadi.
Aga miks peaks täispööre olema just 360 kraadi ja mitte näiteks 100 või 222 kraadi?
Paistab, et see võib seotud olla päevade arvuga aastas – vanasti tundus, et taevased objektid teevad ringi peale umbes 360 ööpäeva jooksul.
Lisaks on arvul 360 kena omadus, nimelt jagub ta väga paljude erinevate arvudega. Kõik järgnevad arvud on tema jagajad, neid on kokku tervelt 24:
Nii saab aastat jagada väga paljudeks erinevateks ühepikkusteks täistsükliteks. Näiteks senini on ju kasutusel 12 kuud, mille pikkused on küll meie teadmiste varal ebaühtlaseks muutunud.
Radiaanid
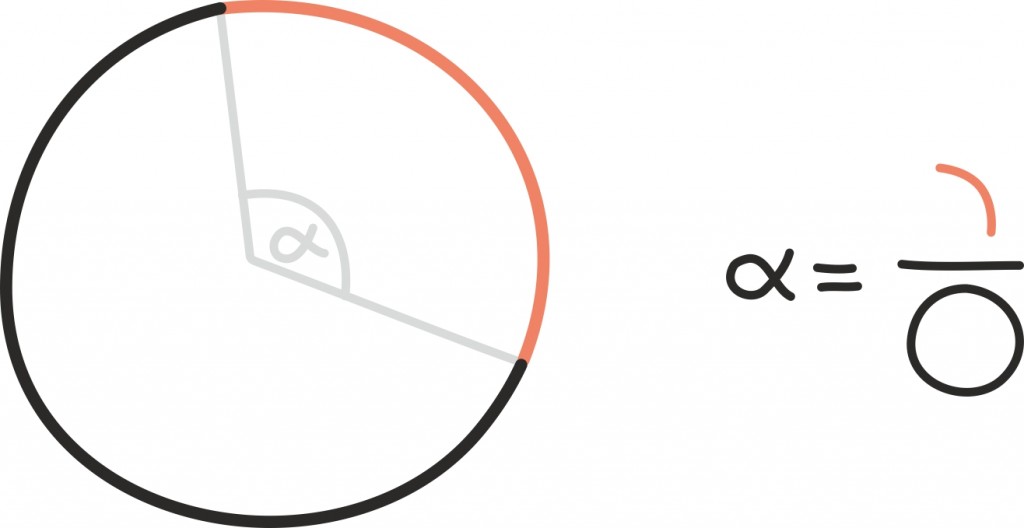
Nurga radiaanmõõdu arvestamiseks on vaja minna ja ringjoone kaare pikkus korralike sammudega ära mõõta – seega on siinkohal tegemist matkamehe nurgamõõduga.
Kui kraadide leidmiseks arvutasime, kui suure osa moodustab nurk täispöördest, siis radiaanide puhul lööme kokku selle ringjoone osa pikkuse, mille moodustab nurga haarade vahele jääv ühikringjoone kaar.
Tuletame meelde, et ühikringjoone pikkus on 2π ning seega on täispöörde suuruseks 2π radiaani. Poole pöörde suuruseks jääb aga näiteks π radiaani.
Ka radiaanide juures on tegelikult mängus teatud meelevaldne valik – miks me pidime just valima ühikringjoone? Kui oleksime oma nurgamõõduks valinud näiteks raadiusega 0,5 ringjoone, osutuks täispöörde suuruseks π radiaani. Kas see poleks kenam? Või oleks hoopis kenam, kui π ise oleks teisiti defineeritud [lk 101]?
Kumba neist ikkagi kasutada?
Tuleme nüüd tagasi peatüki alguses püstitatud küsimuse juurde: kas kasutada kraade või radiaane? Selgub, et see oleneb kontekstist. Nii kaua kui kasutame trigonomeetriat ainult kolmnurkadega tegelemiseks, suurt vahet ei olegi – kraadid ja radiaanid on mõlemad ühtmoodi head ning kasutame neid siin raamatuski läbisegi.
Nii pea kui aga hakkame trigonomeetriliste funktsioonidega tegelema, tuleks eelistada radiaane.
Näiteks radiaane kasutades on siinusfunktsiooni graafiku tõus nullpunkti juures täpselt üks ehk matemaatiliselt:
Tänu sellele ilusale omadusele on näiteks siinusfunktsiooni sin(α) tuletis [lk 320] radiaanide korral cos(α), kraadide korral aga hoopis
Miks see nii peaks olema, näeme juba varsti [lk 251].
Lõpuks ei ole ka väga hullu, kui sõbraga erinevat mõõtu kasutate, radiaanidest kraadidesse ja tagasi viivad lihtsad teisendused. Radiaanidest kraadide saamiseks peame nurga korrutama lihtsalt
ga ning vastupidi kraadidest radiaanide saamiseks korrutama
ga.
Meie oleme seni töötanud kraadidega, aga nüüd lähemegi vahelduseks hoopis radiaanidele üle ja edasi kasutame neid täpselt nii, kuidas tuju on.
Koosinus, siinus ja elastne vedru*
See alapeatükk on skeptilisele ja huvitunud lugejale, kes ei taha uskuda, et pendel on seotud just täpselt siinuse ja koosinusega, mitte mõne muu perioodilise funktsiooniga.
See on igati õigustatud kahtlus!
Õnneks annavad füüsika ja matemaatika käsikäes siiski hea põhjendatud vastuse. Lihtsuse mõttes käsitleme küll siin peatükis hoopis elastset vedru, aga situatsioon ja ideestik on täpselt sama:
- meil on üks keha
- mida liigutab üksainus jõud,
- mis surub objekti tagasi tasakaaluasendisse,
- aga kahjuks liiga tugevasti ning keha jääb võnkuma tasakaaluasendi ümber.
Elastse vedru korral on mõjuvaks jõuks elastsusjõud. Inglise füüsik Hooke tegi 17. sajandil hoolega katseid ja veendus, et mida pikemalt on vedru välja venitatud, seda suurem jõud tõmbab teda kokku ning vastupidi, mida rohkem vedru on kokku surutud, seda suurem jõud lükkab teda jälle lahti.
Hooke oli hoolikas sell ja ta mõõtis ka täpselt välja, kuidas see jõud täpselt vedru väljavenitusest või kokkusurutusest sõltub. Ta tegi kaks järeldust:
- jõud on erinevatest materjalidest vedrude jaoks erinev,
- jõud sõltub täpselt ühtemoodi vedru pikkuse muudust – alati võrdeliselt.
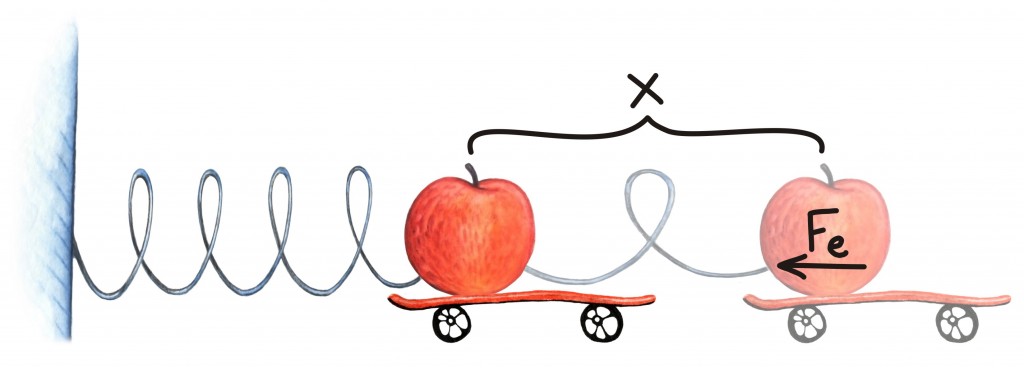
Tähistame nüüd vedru suurusemuutu tasakaaluasendi suhtes x-ga (positiivse x-i korral on vedru välja veninud, negatiivse korral kokku surutud) ning keha materjali jäikust iseloomustavat tegurit k-ga. Sel juhul väidab Hooke’i seadus, et vedru algkujusse kiskuvat elastsusjõudu Fe võib igal ajahetkel t kirjeldada valemiga
Samaaegselt oli Hooke’i kaasaegne ja rahvuskaaslane Newton leidnud veelgi üldisemaid printsiipe meid ümbritseva maailma kirjeldamiseks.
Ta märkas, et kui kehale mõjub mingi jõud, siis keha kiirendus – see, kuidas keha liikumiskiirus muutuma hakkab, – sõltub täpselt võrdeliselt mõjuvast jõust.
Veelgi enam, ta avastas, et mõõtes ka keha massi, võib ta täpselt kirjeldada, kuidas jõud keha kiiruse muutuma paneb: tähistades keha kiirendust a-ga, tema massi m-iga ning kehale ajahetkel t mõjuvat kogujõudu F(t)-ga, võib Newtoni teise seaduse välja kirjutada kujus:
Meie olukorras on ainus vedrule mõjuv jõud igal hetkel antud täpselt eeltoodud elastsusjõuga, mis tema kuju taastada üritab. Gravitatsiooni võime näiteks lihtsalt eirata, kuna horisontaalset liikumist ta ei mõjuta.
Seega võime kirjutada, et vedrule mõjub kogujõud F= Fe, ning valemitest asendades saame
Nii on liikumine igal ajahetkel t kirjeldatud võrrandiga
Selles võrrandis on peidus kaks arvkonstanti m ja k, mis sõltuvad keha omadustest; a(t) ja x(t) kirjeldavad aga igal ajahetkel vastavalt vedru venituse kiirendust ja väljavenituse suurust.
Ometigi on intuitiivselt üsna selge, et ühe objekti kiirendus – tema kiiruse muutumine – on juba olemuslikult ka seotud tema asupaigaga.
Seda seost toob täpsemalt esile tuletise peatükk [lk 320]. Nimelt kiirenduse näol on tegemist läbitud teepikkust või teisisõnu vaadeldava keha asukohta kirjeldava funktsiooni teise tuletisega. Isegi kui tuletis tundub ohtliku sõnana, ei ole selles suurt midagi keerulist – funktsiooni esimene tuletis näitab lihtsalt, kui kiiresti funktsiooni väärtus muutub, ning funktsiooni teine tuletis näitab, kui kiiresti see muutumine ise muutub. Nii ongi näiteks kiirus teepikkuse esimene tuletis ning kiirendus tema teine tuletis.
Seega ütleb meie võrrand, et igal hetkel t on vedru venituse muutumise kiirendus võrdeline tema kogumuutusega:
Võime neid iga ajahetke kohta antud võrrandeid vaadata ka ühe seosena üle kogu aja korraga – seosena ajast sõltuva funktsiooni ning tema teise tuletise vahel.
Sellist võrrandit, mis seostab funktsiooni ja tema tuletisi nimetatakse uhkelt diferentsiaalvõrrandiks – diferentseerimine tähendab ju lihtsalt tuletise võtmist. Nende lahendamine päris käkitegu pole, aga sel korral võib sellega siiski hakkama saada, kui meenutame trigonomeetriliste funktsioonide tuletisi.
Siinusfunktsiooni sin(t) tuletiseks on cos(t) ning sarnasel on koosinusfunktsiooni cos(t) tuletiseks – sin(t).
Need kaks teadmist kokku pannes näeme, et siinusfunktsiooni teine tuletis on – sin(t). Seega rahuldab ta etteantud diferentsiaalvõrrandit, juhul kui
Saamegi ilusa siinuskujulise liikumise, mille periood on täpselt 2π.
Kui aga
on mõne teise väärtusega, peame vastuse leidmiseks muutma oma siinuslaine sagedust kas aeglasemaks või kiiremaks.
Tuleb välja, et üldjuhul on sobivaks lahendiks
Siingi võiks veel nuriseda – sarnaselt sobib ju lahendiks ka koosinusfunktsioon ning veelgi enam, ka koosinus ja siinusfunktsiooni summa! Vedru võngub ju aga ometigi täpselt ühtemoodi, mitte mitut moodi korraga. Tõepoolest, selgub, et puhta siinus- või koosinusfunktsiooni määramiseks tuleb teha veel üks tähelepanek. Nimelt on vedru kiirus kõige suurema väljavenimise ja kokkusurutuse hetkel võrdne nulliga. See tuleneb energia jäävuse seadusest – neil hetkedel on kogu energia muundunud potentsiaalseks energiaks. Seda teadmist arvesse võttes on meie siinusfunktsioon juba üheselt määratud.
Loodame, et nüüd on ka skeptilisem lugeja veendunud, et vedru või ka pendli perioodilise liikumise kirjeldamiseks ei sobi sugugi mitte mingi suvaline siksak või muu perioodiline funktsioon. Sobib just meile juba teada ja tuntud siinusfunktsioon.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!