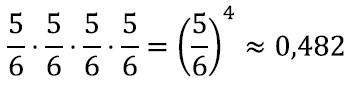Tõenäosusteooria tähendus ja kasutamine
Tõenäosus tundub lihtne ja intuitiivne mõiste. Ühe kindla sündmuse tõenäosus võiks tähendada täpselt seda, kui tihti see konkreetne sündmus juhtub võrreldes teiste, temaga konkureerivate sündmustega.
Teisisõnu tahaksime sümbolite keeles lihtsalt defineerida:
See definitsioon on siiski üsna hägus, sest ta jätab vastamata päris paljudele küsimustele.
- Milliseid teisi sündmuseid me sageduse arvutamiseks arvesse peaksime võtma? Koduõues täringuga kuue viskamine ei ole ju kuidagi seotud näiteks kaardipaki segamisega Austraalias, aga on seotud sama täringuga kahe või kolme viskamisega.
- Kui palju vaatlusi on vaja teha, et võiksime sündmuse sageduse mõistlikult välja arvutada? Ilmselt ühest vaatlusest ei piisa – sel juhul võiks ju tõenäosus olla ainult null või üks. Aga kas näiteks kolmesajast on küll?
- Mida teha sündmustega, mis võivadki juhtuda ainult maksimaalselt üks kord? Tahaksime ju võrrelda tõenäosuseid, et üks või teine meie sõber saab presidendiks, või isegi rääkida tõenäosusest, et maaväline elu eksisteerib. Sageduse abil tõenäosusest mõtlemine on sel juhul üsna selgelt raskendatud.
Selgub, et hoolimata nendest küsimustest on tõenäosus igati mõistlik idee väga paljudes erinevates olukordades. Tema käsitlus nõuab küll tõesti natuke rohkem täpsust, kui alguses välja pakutud idee. Järgnevalt selgitame mõne loo abil, kuidas tõenäosusest võiks mõelda, kuidas teda võib elu kirjeldamisel rakendada ning milliseid ohte mõlemal juhul silmas tuleks pidada.
Väike mündilugu ehk mida tõenäosus ikkagi tähendab?
Hans ja Grete istuvad keset metsa pimedavõitu onnis. Hans, keda pimeduses istumine järsku ära tüütab, süütab salaja kaasa võetud küünla, võtab taskust välja särava mündi ning hakkab Gretet tõenäosusteooriaga kiusama.
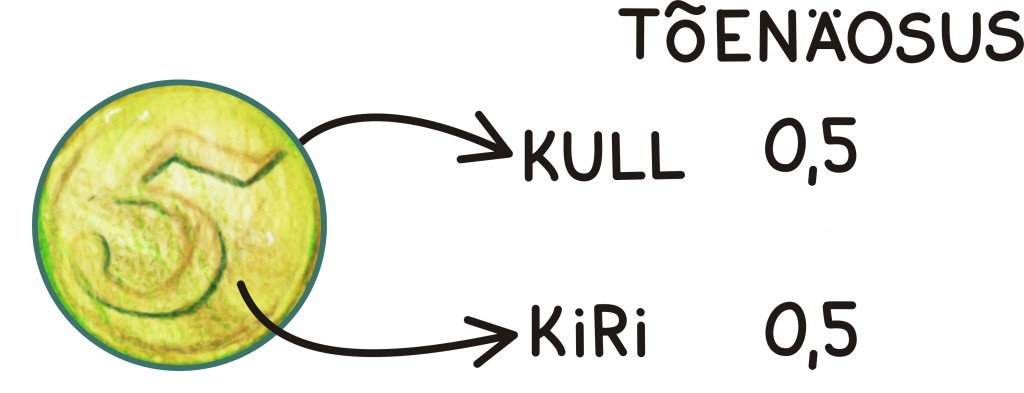
Hans: Grete, mis on tõenäosus, et ma nüüd viskan oma mündiga kulli ja mitte kirja?
Grete: Kallis Hans, kindlasti hakkad mind nüüd kavaldama, aga praegu arvan küll, et kull ja kiri on täiesti võrdväärsed ning seega on tõenäosus täpselt pool.
Hans viskab sõnagi lausumata münti, aga kohe, kui münt käeseljale maandub, katab ta teise käega, nii et tulemust ei näe ei Grete ega Hans isegi.
Hans: Aga nüüd, Grete, mis on tõenäosus, et siin käe all varjus olev münt varjab kulli?
Grete: Ma ei ole harjunud niimoodi tõenäosusest mõtlema – münt on ju juba visatud, nüüd tal kas on kull pealpool või ei ole. Kuidas ma nii tõenäosusest üldse rääkida saan?
Hans: Aga kas sa oleksid nõus näiteks kihlveoga, kus ma annan sulle kaks šokolaadi, kui tegemist on kulliga, ning sina mulle ühe, kui tegemist on kirjaga?
Grete: See tundub sinust palju lahkem kui tavaliselt. Ma oleksin nõus küll. Sa tead sama vähe kui mina, meie mõlema meelest võiks praegu mündi peal olla sama hästi nii kull kui kiri… Seda sa vist mõtlesidki tõenäosuse all? Minu meelest on tõenäosus, et münt on kull, endiselt pool.
Hans: Väga hea, Grete, väga hea.
Hans piilub nüüd ise münti ja ütleb Gretele, et tegemist on kulliga, ent ei näita seda veel Gretele.
Hans: Mis on Sinu meelest nüüd tõenäosus, et münt on kull?
Grete: Münt ise on ammu juba visatud ja nüüd sa ju just ütlesid, et see on kull, kuidas ma siis saan veel tõenäosusest rääkida?
Hans: Aga Grete, enne ütlesin ma ka sulle, et mul ühtegi küünalt ei ole, sest tahtsin natuke aega sinuga pimedas olla.
Grete: Seega sa võiksid jälle valetada nagu enne?
Hans: Võiksin.
Grete: Münt on visatud, ta on kas kull või kiri, sina juba tead tulemust, ütled mulle, et tegemist on kulliga, ja nüüd peaksin mina ütlema, mis on tõenäosus, et tegemist on kulliga. Ma ei saa enam midagi aru.
Hans: Mõtle, Grete, muidu kustutan küünla jälle ära!
Grete: Ma proovin ju. Kui sa mulle kunagi ei valetaks, siis oleks tegemist kindlasti kulliga ja tõenäosus oleks seega üks. Kui sa kogu aeg valetaksid, oleks tegelikult kiri ülalpool ning kulli tõenäosus oleks null. Kui sa ajaksid kogu aeg täiesti suvalist juttu, siis võiksin sinu ütlust ignoreerida ja tõenäosus oleks jälle pool. Aga…
Hans: Aga vahepeal ma ikka räägin tõtt ka. Näiteks siis, kui ütlesin, et oleme kadunud.
Grete: Jah, kahjuks või õnneks küll. Seega tõenäosus, kas münt on kull või mitte, on nüüdseks hoopis tõenäosus, kas sa räägid tõtt või mitte.
Hans: Väga tubli, Grete. Kas sa seda tõenäosust tead?
Grete: Ei tea.
Hans: Aga kas sa saaksid seda kuidagi leida?
Grete: Kui ma oleksin kõik meie jutuajamised lindistanud ning seejärel loeksin pärast kokku, kui palju kordi sa oled valetanud ning kui palju tõtt rääkinud, siis võiksin seda tõenäosust vähemalt hinnata.
Hans: Grete, lindistamine ei ole ilus, Edgar korra juba proovis.
Grete: Tõsi, Hans, aga mis on see tõenäosus, et ka mina vahele jääksin?
Sulle võivad huvi pakkuda need õppematerjalid:
Peastarvutamine I kooliastmele
Liitmine ja lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruutjuur, tehted ruutjuurtega
Ratsionaalavaldised
Algebralised murrud
Tasandilised kujundid
8. klassi matemaatika teooriavideod
Liitmine 20 piires
Geomeetria
Kirjalik liitmine
Funktsioonide graafikute lõikepunktide leidmine
Kirjalik lahutamine
Peastarvutamine eelkoolile
Ruumilised kujundid
II kooliastme matemaatika reeglite kordamine
Lahutamine 20 piires
Ruutvõrrand
Funktsioonide graafikud
Harjutusülesandeid matemaatika riigieksamiks
Järelnoodid
Tõenäosustest rääkides peab olema väga hoolikas, mis sündmuse tõenäosusest just parasjagu räägime. Iga tõenäosuslik kirjeldus on tegelikult lihtsustus maailmast – me ei tea täpselt, mis juhtub, aga tahame seda ennustada või kirjeldada. Tõenäosusliku kirjelduse jaoks loetleme sündmused, mis juhtuda võiksid, ning anname neile hinnangud, kui tihti üks või teine neist juhtub. Need hinnangud ongi sisuliselt niinimetatud tõenäosused.
Nagu nägime, sõltub nende hinnangute või tõenäosuste määramine meie enda teadmistest. Kui teame, et münt on sümmeetriline, võiksime hinnata, et kulli või kirja viskamine on täpselt pool.
Kui aga teaksime, et ta on natukene vildakas, on selle hinnangu andmine palju raskem – peaksime ilmselt tegema enne sadu viskeid ning selle põhjal tõenäosust hindama. See hinnang jääks aga alati ligikaudseks ja peegeldaks lihtsalt meie tolle hetke teadmist.
Tõenäosusteooria algus ehk kuidas valed arvutused viivad pankrotti
Tõenäosusteooria algusloo kohta on liikvel huvitav legend. Selle legendi kohaselt ei ole tõenäosusteooria aluskiviks sugugi intellektuaalne huvi, vaid hoopis kirglik hasartmäng. Nimelt hakkas paadunud ja tunnustatud hasartmängur ning amatöörmatemaatik Chevalier de Méré (1607–1684) enda loodud reeglitega järsku täringumängus pidevalt kaotama.
Probleemile lahenduse leidmiseks otsustas ta kirjutada ühele oma heale sõbrale, kuulsale prantsuse matemaatikule ja filosoofile Blaise Pascalile (1623–1662). See 17. sajandil kirjutatud murekiri panigi praeguse arusaama kohaselt aluse tõenäosusteooria arengule.
Oma kirjas kurtis Chevalier de Méré Blaise Pascalile, et täringutepaar, mis oli talle sisse toonud hulgaliselt raha, on nüüd järsku hakanud alt vedama.
Algupäraselt oli kihlvedu järgmine: Chevalier de Méré väitis, et ta suudab nelja viskega raudselt vähemalt korra kuue visata. Kirja autorile tundus loogiline, et sellise kihlveoga peaks rohkem võitma kui kaotama, ning aja jooksul saadud võidud aina süvendasid seda uskumust. Kui alguses leidus tublisti huvitunud mängijaid, kes olid oma kuueviskamisandes kindlad, ei jätkunud kihlvedusid siiski kuigi kauaks – Chevalier de Méré pidevad võidud kahandasid kiiresti nende inimeste arvu, kes mänguga soostusid.
Nii otsustas Chevalier de Méré mängureegleid muuta. Nüüd väitis ta, et suudab täringupaari viskega saada vähemalt korra topeltkuued. Ta oli veendunud, et siingi peaks kihlvedu tema kasuks olema. Ometigi hakkas aga vaene Chevalier de Méré aina kaotama…
Kuna temagi argumendid olid ta enda meelest üsna matemaatilised, läks ta oma tusatujus nii kaugele, et kuulutas matemaatika ja päriselu vahelise suhte olematuks. Nagu kohe näeme, matemaatika temaga siiski päris nõus ei ole.
Mida arvab Chevalier de Mere kihlvedudest matemaatika
Chevalier de Méré väitis, et ta suudab:
- visata nelja täringuga vähemalt ühe kuue,
- visata kahekümne nelja täringupaariga vähemalt korra topeltkuued.
Esimese kihlveoga oli ta rikkaks saamas, ent teisega mängis oma varanduse kärmelt maha. Chevalier de Méré oleks nende kihlvedudega raha kokku ajanud parajasti siis, kui ta oleks rohkem kui pooltel kordadel suutnud oma lubatut täita.
Kuidas oleks ta võinud ette juba aimata, kui tihti ta võidab või kaotab?
Üks võimalus oleks olnud leida täringuviskele tõenäosuslik kirjeldus. Nimelt, üks tõenäosuse tõlgendus on ju just nimelt sageduslik – tõenäosus näitab, kui tihti üks või teine sündmus meie kirjelduse kohaselt pikas perspektiivis juhtub. Rohkem kui pooltel kordadel tähendab seega, et selle sündmuse tõenäosus on suurem kui pool.
Näeme, et armas hasartmängur pidanuks rikkaks saama parajasti siis, kui tal oleks olnud täringuviskest täpne kirjeldus ning mõlema tema lubaduse tõenäosus selles kirjelduses oleks olnud poolest suurem.
Täringuviske tõenäosuslik kirjeldamine on üsna lihtne. Nii kaua kui mäng on aus (ja vaevalt et petturiga keegi täringuid viskaks!) on mõistlik eeldada, mõelda või postuleerida, et kõik täringu küljed on võrdväärsed – on võrdne võimalus, et viskel tuleb ükskõik milline külgedest. Seega on kõikide nende tõenäosus täpselt 1⁄6.
Esimese kihlveo korral on soodsaks sündmuseks see, et visatakse nelja viske jooksul vähemalt korra üks kuus. Selgub, et lihtsam on aga arvutada selle sündmuse vastandsündmuse tõenäosust – ehk siis sündmuse, et igal viskel visatakse üks kuni viis silma, tõenäosust. Nimelt piisab sel juhul iga viske eraldi uurimisest ja nende sidumisest sõltumatute sündmuste reegli abil.
Tõenäosus, et ühel viskel viskame üks kuni viis silma, on 5⁄6. Kõik visked on aga omavahel sõltumatud ning võime nende tõenäosused kokku korrutada, leidmaks tõenäosus, et me ei viska ühtegi kuut. See on parasjagu
Kuna vastandsündmuste tõenäosuste summa on üks, siis järeldame, et vähemalt ühe kuue viskamise tõenäosus on umbes 0,518 ehk rohkem kui pool. Siit tulevad võidud!
Ka teise kihlveo korral on lihtsam välja arvutada vastandsündmuse tõenäosust – tõenäosust, et igal täringupaari viskel ei saada topeltkuut. Iga sellise viske tõenäosus on täpselt 35⁄36, kuna kokku on 36 võimalikku paari. Seega leiame, kasutades jällegi sõltumatute sündmuste reeglit, et mitte ühegi kuute paari viskamise tõenäosus on
See on aga rohkem kui pool! Seega on ühe 12 silmaga täringupaari viskamise tõenäosus omakorda vähem kui pool ning selge see, et härra de Méré oma rahast ilma jäi.
Matemaatika igal juhul süüdi pole!
Mille vastu Chevlier de Méré siis eksis? Selle asemel, et hoolsalt arvutada (peab tunnistama, et tol ajal ei olnud muidugi arvude 24. astme leidmine nii väga lihtne), uskus ta oma intuitsioonil põhinevat mõtteviisi. Ta arutles, et kahe kuue viskamine kahel viskel on 6 korda vähem tõenäoline kui ühe kuue viskamine ühel viskel ja et seega tuleb 6 korda rohkem viskeid teha, et seda kompenseerida. Kõlab isegi päris usutavalt?
Kas mu sõbrannast saab riigikogu liige ehk tõenäosuste määramise raskustest
Tore oleks vahel Toompeal teed juua. Üks võimalus selle unistuse realiseerumiseks on see, kui parimast sõbrannast saab Riigikogu liige. See ei ole sugugi kindel, aga päris võimatu ilmselt ka mitte. Kas sellele on võimalik mingi mõistlik tõenäosuslik hinnang anda?
Selle jaoks oleks meil vaja jällegi mingit tõenäosuslikku kirjeldust. Kõige lihtsam võimalik kirjeldus tegelebki ainult lõpptulemusega: meie sõber kas saab või ei saa Riigikogu liikmeks, seega on meil täpselt kaks elementi, millele tahaksime tõenäosused külge pookida. Lisaks peaks nende tõenäosuste summa olema veel üks – seega sisuliselt jääb hinnata ainult üks arv.
Kogu raskus on aga neile võimalustele tõenäosuste määramises. See ongi ju täpselt meie küsimuse ümbersõnastus! Kuidas neid tõenäosuseid määrata?
Võrdväärsuse eeldus siin kehtivat ei paista – tundub siiski tõenäolisem, et sõbrannast ei saa Riigikogu liige. Seega pool ja pool peame ilmselt välja jätma.
Ka statistika ei paista kohe kaasa aitavat: meil on ju üks konkreetne sõbranna ja temaga saame katset teha täpselt ühe korra ja see katse saab läbi alles mitmekümne aasta pärast!
Seega selgub, et meie matemaatiline mudel on liiga täpne – peame seda hajusamaks muutma, et üldse midagi öelda või ennustada.
Üks viis selle tegemiseks on sõbra unikaalsusest loobuda. Võiksime küsida hoopis: mis on tõenäosus, et mõni neiu saab Riigikogu liikmeks? Siin võiksime küll kõik Eesti naiskodanikud kokku arvata ja vaadata, paljud neist on saanud Riigikogu liikmeteks, ning hinnang olekski käes!
Aga ometi, meie sõbranna ei ole ju lihtsalt üks tavaline eestlanna. Tal on näiteks punane pea. Ehk mängib see olulist rolli, ehk peaksime ka seda arvesse võtma? Või seda, et ta on väga tark? Kuidas seda otsustada?
Ideaalis tuleks teha statistikat! Otsustada, millised omadused (juuksevärv, haridus, jalanumber jpt) mängivad rolli Riigikogusse valimisel ja millised ei mängi. Liiga palju omadusi arvesse võtta ei saa – muidu jõuaksime jälle olukorda, kus ainult meie sõbrannal ongi kõik need omadused. Samas, liiga vähe omadusi arvesse võttes oleksime liiga ebatäpsed.
Hea tõenäosusliku kirjelduse ning sinna sobivate tõenäosuste leidmine on väga raske. Mõnikord üritatakse sellest üle hüpata ja mitte täpsustada, mille kohta täpselt tõenäosuslik kirjeldus käib, või jätta teatamata, kust on tõenäosused ise võetud – on nad pärit eeldustest, on nad pärit mingitest andmetest, millistest andmetest nad pärit on.
Näiteks kui reklaam ütleb, et hambapasta tapab 99% bakteritest, siis mida see tähendab? Mis on see tõenäosuslik kirjeldus seal taustal?
Kas see tähendab, et bakterikultuuridele pandi mitmeid kordi peale hambapastat ning 99% juhtudest tapeti kõik bakterid? Milliseid baktereid sel juhul üldse kasutati, kas neid, mis on suus, või suvalisi, mis ehk kannatavad vähem fluori? Millises keskkonnas neid kasvatati? Miks see peaks üldistuma suukeskkonnale?
Või äkki mõõdeti tõesti bakterite arvu suus enne hambapesu ja pärast hambapesu ning iga kord oli pärast pesu alles 1% baktereid? Kas alati just täpselt 1% või keskmiselt 1%?
Arv 99% on ilus, aga mida ta ikkagi tähendab?
Kes on kõrgema IQ-tasemega ehk jaotuste võrdlemine
Oletame, et mingil kummalisel põhjusel tahaksime omavahel võrrelda mehi ja naisi või noori ja vanu. Üldiste järelduste tegemiseks ei piisa sel juhul mõne konkreetse paari tulemuste või mõõtude võrdlemisest. Näiteks selle jaoks, et öelda, kas mehed või naised on pikemad, ei saa ju võtta lühimat meest ja pikimat naist. Tuleb ikka ühte patta panna andmeid paljude meeste kohta, teise andmeid paljude naiste kohta ning võrrelda nende padade sisusid.
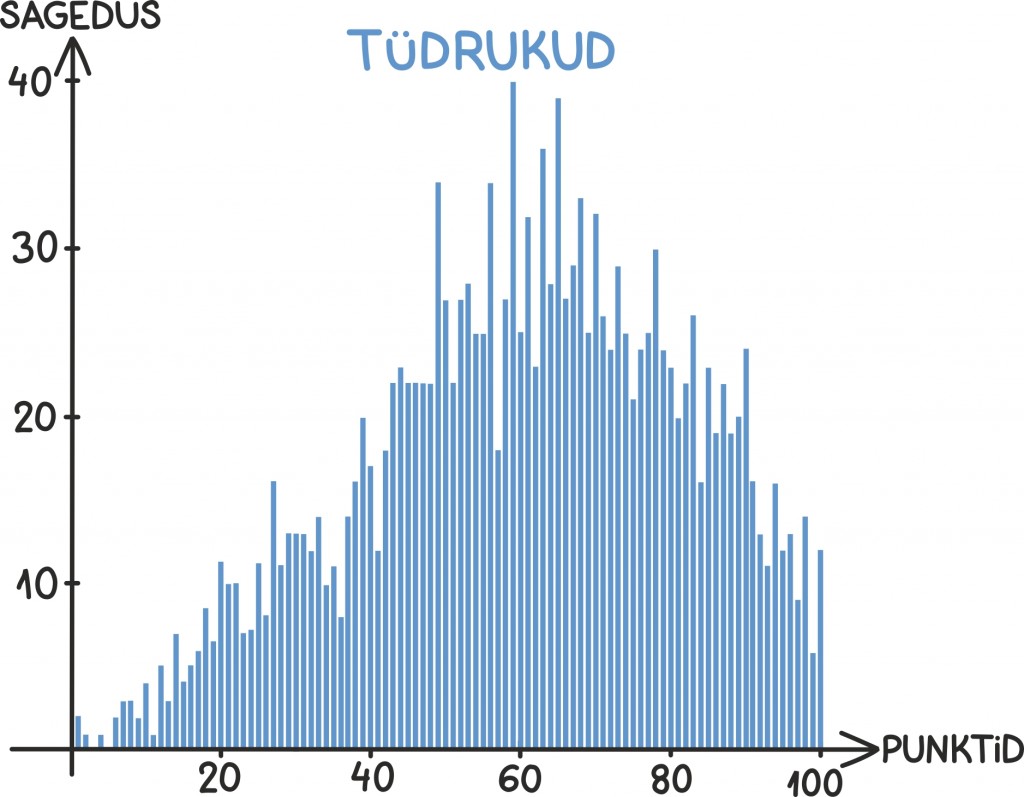
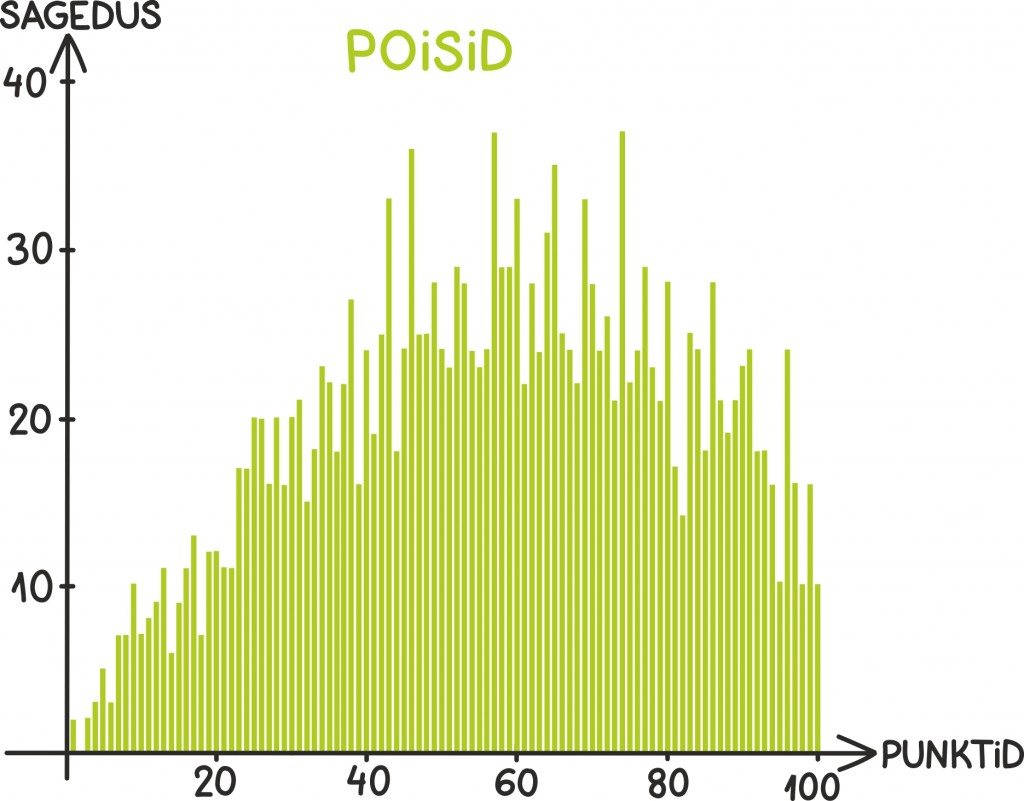
Kõiki andmeid ühes pajas koondabki endas tõenäosus- või sagedusjaotus. Tihti esitatakse neid jaotuseid graafiliselt, histogrammi abil, mis näitabki, kui sagedasti üks või teine sündmus juhtus. Näiteks siin on hirmutamiseks toodud matemaatika eksamitulemuste jaotus eraldi poiste ning tüdrukute jaoks:
Kuna jaotuste kõrvutamisel ei võrdle me enam kahte arvu, vaid kahte pajatäit arve, pole see kõrvutamine ega selle põhjal järelduste tegemine enam sugugi nii lihtne ja ühene.
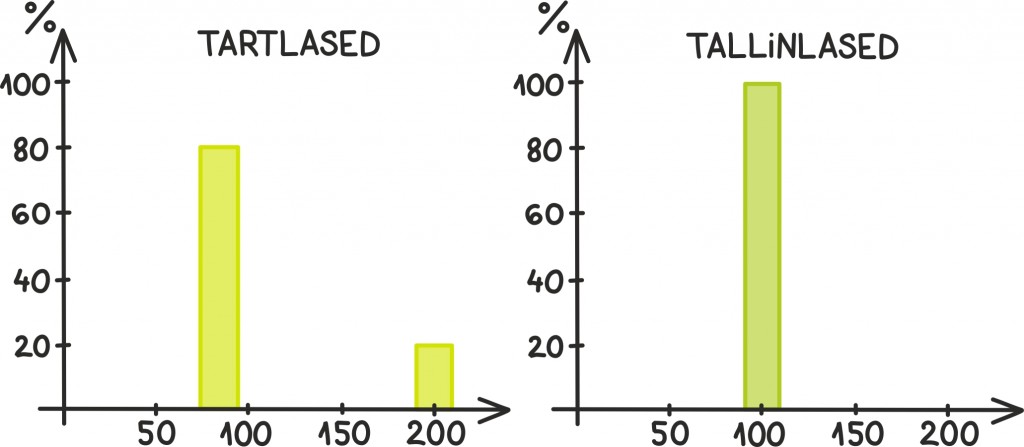
Näiteks oletame, et meil on kaks hõimu „tartlased” ja „tallinlased” ning meil on teada mõlema hõimu kõikide liikmete IQ-testi tulemus. Hõimus „tartlased” on 20% inimestest IQ 200 ning 80% IQ 80. Hõimus „tallinlased” on kõikidel võrdselt IQ 100.
Kumb hõimudest on kõrgema IQ-tasemega?
Ühelt poolt on hõimus „tartlased” keskmine IQ-tase: 0,2 · 200 + 0,8 · 80 = 104 ning hõimus „tallinlased” vaid 100. Teiselt poolt on kõik hõimu „tallinlased” liikmed kõrgema IQ-tasemega kui tervelt 80% hõimu „tartlased” liikmetest.
Selgub, et meie küsimus on liiga ebatäpne: mida me ühe hõimu kõrgema IQ-taseme all silmas pidasime? Seda, et tema keskmine IQ-tase on kõrgem? Et suurema osa tema liikmete IQ-tase on kõrgem? Et hõimu minimaalne või maksimaalne IQ-tase on kõrgem? Või et kõik need parameetrid on kõrgemad? Need on kõik erinevad küsimused ning vastused võivad olla vastukäivad.
Tihti ongi kõige lihtsam jaotuseid võrrelda nende graafikute põhjal. Nii on lihtne märgata, kummas jaotuses on suuremad maksimumtulemused, kuhu umbes jääb keskmine tulemus ja nii edasi. Kohe võib ka silma jääda, et mingit mõistlikku võrdlust ei saagi teha.
Geomeetriline tõenäosus ehk kuidas leida tõenäosuse abil pii väärtust
Koolipingis räägitakse ka millestki, mille nimi on geomeetriline tõenäosus. Geomeetriline tõenäosus ei ole matemaatilise tõenäosuse alternatiiv, tegemist on lihtsalt veel ühe viisiga, kuidas tõenäosust tõlgendada ning mille raames ka küsimusi esitada. Ka siin üritame teatud sündmusi kirjeldada ja nende mahtu mõõta, teeme seda lihtsalt geomeetria abil.
Kahemõõtmelises maailmas põhineb geomeetriline tõenäosus pindaladel. Tõlgendame kõike võimalikku, mis juhtuda võiks, mingi piiratud tasanditükiga ning meid huvitavat sündmust mingi kujundiga selle tüki piires. Selle sündmuse tõenäosuse saaksime siis täpselt, leides meid huvitava kujundi ning kogu tasanditüki pindalade suhte.
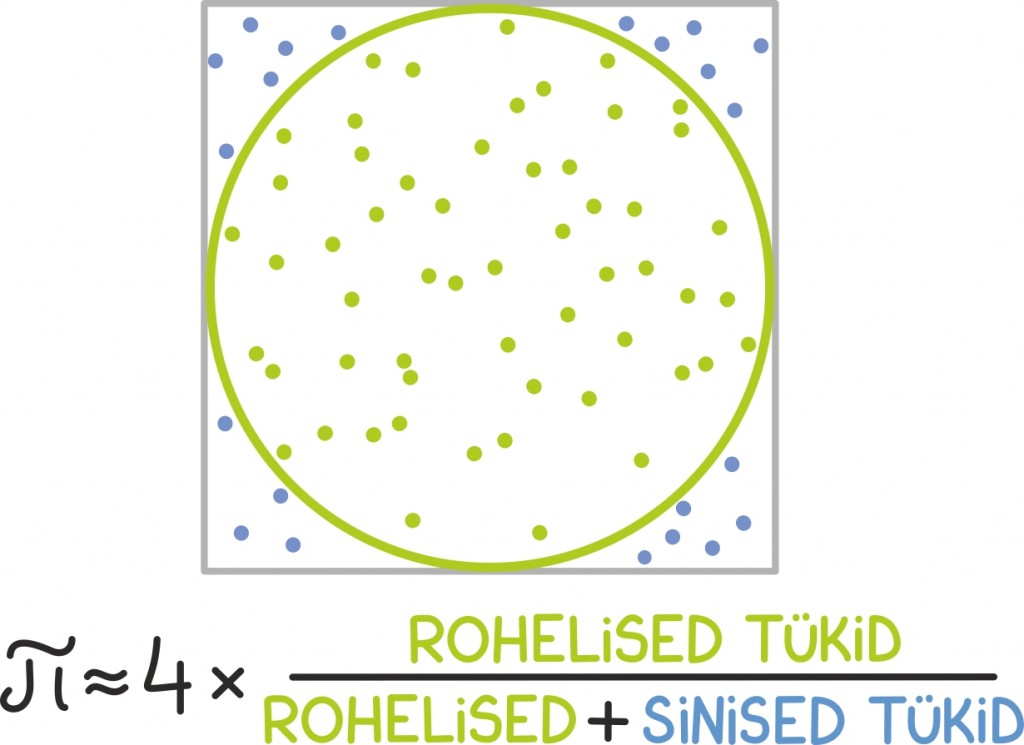
Seda meetodit või tõlgendust ümber pöörates võiksime näiteks leida hea lähenduse π [lk 99] väärtusele. Nimelt joonistame ruudukujulisele põrandajupile mõõtmetega 1 m korda 1 m siseringjoone nii nagu joonisel näidatud.
Sel juhul on ringjoone sisse jääv pindala
ning ruudu pindala täpselt 1.
Oletame nüüd, et meil õnnestub lae alt kukutada paberitükikesi, nii et nad kukuvad selle ruudu raames enam-vähem ühtlaselt juhuslikult. Kui ruut on piisavalt väike ning lagi piisavalt kõrge, peaks see üsnagi võimalik olema.
Nüüd, ühelt poolt teame, et ringi ja ruudu pindalade suhe on
ning seega on ringjoone sisse kukkumise tõenäosus täpselt
Teisalt võime seda tõenäosust hinnata, niipea kui oleme kukutanud mõned paberilipakad. Neid piisavalt palju kukutades saame tegelikult väga hea hinnangu ka π väärtusele!
Joonisel võib seda kõike kujutada umbes nii:
Seesama protseduur ja idee on ka aluseks Monte Carlo integreerimisele [lk 349]. Sel juhul ei visata lihtsalt enam paberilipakaid, vaid juhuslikud punktid genereeritakse arvuti abil.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!