PROTSENDI LEIDMINE ARVUST
Mõnikord esitatakse osa leidmisel arvust osamäär protsentides. Protsendi tähis ehk märk on %. Tervik on 1 ehk 100%. Osale vastava osamäära võib esitada hariliku murruna, kümnendmurruna või protsendimäära abil. Protsendimäär on osamäär, mis on korrutatud 100ga.
N: Osamäär 0,2 on protsendimäärana 20 ja protsentides esitatult 20%.
Sulle võivad huvi pakkuda need õppematerjalid:
Algebralised murrud
Funktsioonide graafikute lõikepunktide leidmine
Funktsioonide graafikud
Ratsionaalavaldised
Liitmine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruutvõrrandi abil lahenduvad tekstülesanded
Protsendi rakendused igapäevaelus
Liitmine ja lahutamine 10 piires
Liitmine ja lahutamine 20 piires
Peastarvutamine I kooliastmele
Hariliku murru kordamine
Tasandilised kujundid
Kirjalik lahutamine
Üksliikmed, hulkliikmed ja tehted nendega
Peastarvutamine eelkoolile
Väike protsendiamps
8. klassi matemaatika teooriavideod
Numbrilised seosed
Protsendid põhikooli matemaatikas
Osamäära kujutamise viisist ei olene ülesande lahendamise käik. Kui osamäär on antud protsentidena, tuleb see arvutamisel teisendada murdarvuks (harilikuks murruks või kümnendmurruks).
N: Leia 20% arvust 80. Teeme joonise: 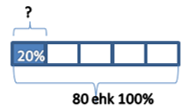
Protsentülesannete lahendamisel:
- Loe ülesanne tähelepanelikult läbi ja selgita, mis on ülesandes antud ja mida tuleb leida.
- Soovituslik on koostada teksti põhjal joonis – see annab parema ülevaate ülesande andmetest ja seostest. Pea meeles, et 1 tervik on 100%.
- Seejärel koosta lahendusplaan ja lahenda ülesanne.
Protsentülesannete lahendamiseks on mitu võimalust: ühe protsendi kaudu või osamääraga korrutamise teel.
Protsentülesanded:
Lisainfo
Protsentülesanded
Vaatleme järgmisi protsentülesandeid:
- a) osa leidmine tervikust;
- b) terve leidmine osa järgi;
- c) mitu protsenti moodustab üks arv teisest;
- d) suuruse kasvamine ja kahanemine protsentides.
Et 1% on üks sajandik tervest, siis ilmselt k% on k sajandikku tervest.
Näide 1. Leiame 67% 420-st.
Eelneva põhjal tuleb leida korrutis
Näide 2. Lattu veeti sügisel 420 tonni kartuleid ja neist oli kevadeks mädanenud 33%. Ülejäänud kartulid õnnestus omanikul maha müüa. Mitu kilogrammi kartuleid müüdi?
Kui kartulitest mädanes 33%, siis müügiks kõlbulikke oli järelikult 100% – 33% = 67%. Seega leiame 67% 420-st. See on aga juba eelmises ülesandes välja arvutatud. Seega oli müügikõlbulikke kartuleid 281,4 tonni.
Terve leidmisel osa järgi pannakse andmed tihtipeale kirja võrde kujul (saab ka teisiti).
Näide 3.Leiame arvu, millest 34% on 77.
Kui 34% on 77, siis
100% on x,
Näide 4. On teada, et 34% mingist arvust x on 68. Leia 71% sellest arvust.
Selle ülesande lahendamisel polegi tarvis teada, kui suur x on, sest ülesande saame lahendada jällegi võrde abil.
34% vastab 68 -le
71% vastab y,
millest
Ülesande võib lahendada ka nii, et kõigepealt leiate arvu x ja siis sellest 71%.
Kui on tarvis teada, mitu % moodustab üks arv teisest, siis leitakse nende jagatis ja tulemus korrutatakse 100%-ga.
Näide 5. Ühes külas elas 200 elanikku. Neist 7 olid koeraomanikud, 34 inimest oli abielus ja talupidajaid oli 8. Leia vallaliste osakaal selles külas.
Et abielus olevaid inimesi oli 34, siis vallalisi on järelikult 200 – 34 = 166. Leiame nüüd vajaliku suhte
(166 : 200) 100% = 83%.
Suuruse kasvamise ja kahanemise kohta vaatame järgmisi näiteid.
Näide 6. Mart kaalus enne koolivaheaega 66 kg ja oli suvepuhkuselt tulles 77 kg raskune. Kui mitme protsendi võrra kaal suurenes?
Kaalu suurenemine on 77 – 66 = 11 (kg). Nüüd leiame, mitu kg on 11 66-st (esialgsest kaalust).
Näide 7. Marta kaalus esmaspäeval 102 kg, kuid ta asus hoolega trenni tegema ja toitus targalt, kaaluvähendavalt. Selle tulemusena vähenes tema kaal kolme kuuga 92 kilogrammini. Kui mitu protsenti kaal vähenes?
Kaalu vähenemine on 102 – 92 = 10 (kg). See moodustab esialgsest kaalust
Vaatleme nüüd veel mitmesuguseid ülesandeid protsentarvutuse kohta.
Näide 8. Peetril oli 5 liitrit 90% piiritust ja tahtis saada 40% segu. Kui mitu liitrit ta peab vett lisama, et soovitud segu saada?
Kõigepealt leiame, kui suur osa on 90% piirituses puhast (st 100%) piiritust (jätame arvestamata selle, et sellist piiritust pole praktiliselt olemas).
Puhast piiritust on seega 4,5 liitrit (90% 5-st).
Edasi lähtume sellest, et
Kui me lisame x liitrit vett, siis puhast ainet on ikka 4,5 liitrit ning kogu lahust on 5 + x liitrit. Seega lahendame võrrandi
ehk x = 6,25.
Seega tuleb vett lisada 6,25 liitrit.
Näide 9. Emmanuel Saba laenab oma vennalt Peeter Sabalt 20 000 krooni intressimääraga 22% aastas. Kuna aga Emmanueli majandustegevus oli edukas, siis suutis ta laenu juba 9 kuu pärast tagasi maksta. Kui suur summa tuli Emmanuelil tasuda?
Tagasi tuleb maksta laen ja intressid.
Laenusumma on 20 000 eurot.
Kuna aga laen ei olnud aasta pikkune, vaid ainult 9 kuud sellest, siis ei lisandu intresse mitte 22%, vaid ainult 3/4 sellest (9 kuud on 3/4 aastat).
Seega tuleb intresse maksta
3 300 eurot
Tagasi tuleb maksta ühtekokku 23 300 eurot.
Lisainfo autor: Allar Veelmaa, Taskutarga jaoks toimetanud: Inge Vestrik
Allikas: Protsentülesanded
TEST:
Protsentülesanded. Vali õiged vastused
Harjuta:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!































