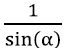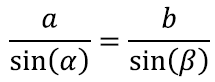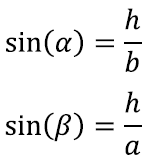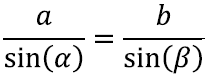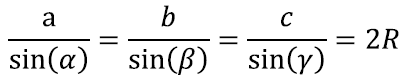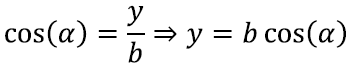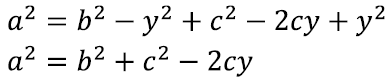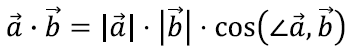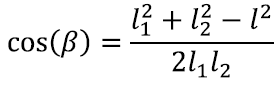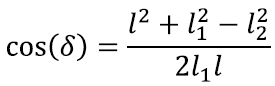Proportsioonid ja kolmnurgad
Küsimus kosmosest
Oletame, et pärast keskkooli pääsed tööle kosmosejaama. Milline rõõm, kosmosejaam!
Kosmosejaam on aga katki ja vajab paikamist ühe antenni otsa juurest. Seega tuleb välja saata astronaut ja ta õigesse kohta toimetada. Kuidas kosmonauti avakosmoses liigutada?
Tänases kosmosejaamas on astronautide liigutamine lahendatud mitmeosalise robotkäe abil, mille moodustavad pööratavad liigesed ja sirged jupid – just nagu inimkäegi.
Kuidas seda robotkätt kontrollida? Kuidas välja arvutada, kui palju ja kuidas erinevaid liigeseid pöörata, et astronaut õigesse paika viia ja jaam ära paigata?
Selgub, et siin tuleb appi kolmnurga elementide ühendamine trigonomeetria abil. Tõepoolest, lihtsamale juhule leiad lahenduse käesoleva peatüki lõpust.
Rännakut trigonomeetriasse alustame aga väikese sissejuhatusega kolmnurkadesse.
Sulle võivad huvi pakkuda need õppematerjalid:
Peastarvutamine I kooliastmele
Harjutusülesandeid matemaatika riigieksamiks
Ruutjuur, tehted ruutjuurtega
Lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Kell ja kellaaeg
Tasandilised kujundid
Ratsionaalavaldised
Geomeetria
Liitmine ja lahutamine 20 piires
Funktsioonide graafikute lõikepunktide leidmine
Liitmine 10 piires
Ruutvõrrand
Kirjalik liitmine
Üksliikmed, hulkliikmed ja tehted nendega
Kirjalik lahutamine
Ruutvõrrandi abil lahenduvad tekstülesanded
Väike protsendiamps
II kooliastme matemaatika reeglite kordamine
xy-koordinaatsüsteem
Võrdsed ja sarnased kolmnurgad
Nagu juba raamatu esimeses osas mainisime, on kaks kolmnurka võrdsed või uhkemalt öeldes kongruentsed siis, kui neid võib täpselt üksteise peale asetada, kusjuures seejuures on lubatud kolmnurk ka tasandilt välja tõsta ja teistpidi pöörata.
Kahe kolmnurga kongruentsuse garanteerib näiteks kõigi kolme külje võrdsus. See kõlab esialgu üsna lihtlabaselt, aga tegelikult vajab tõestamist.
Tõepoolest, näiteks sellest, kui kõik kolm nurka on võrdsed, kolmnurkade endi võrdsus ju ei järeldu, sest kolmnurgad võivad olla erineva suurusega.
Samuti ei järeldu nelinurkade puhul kõige nelja külje võrdsusest nelinurkade kongruentsus.
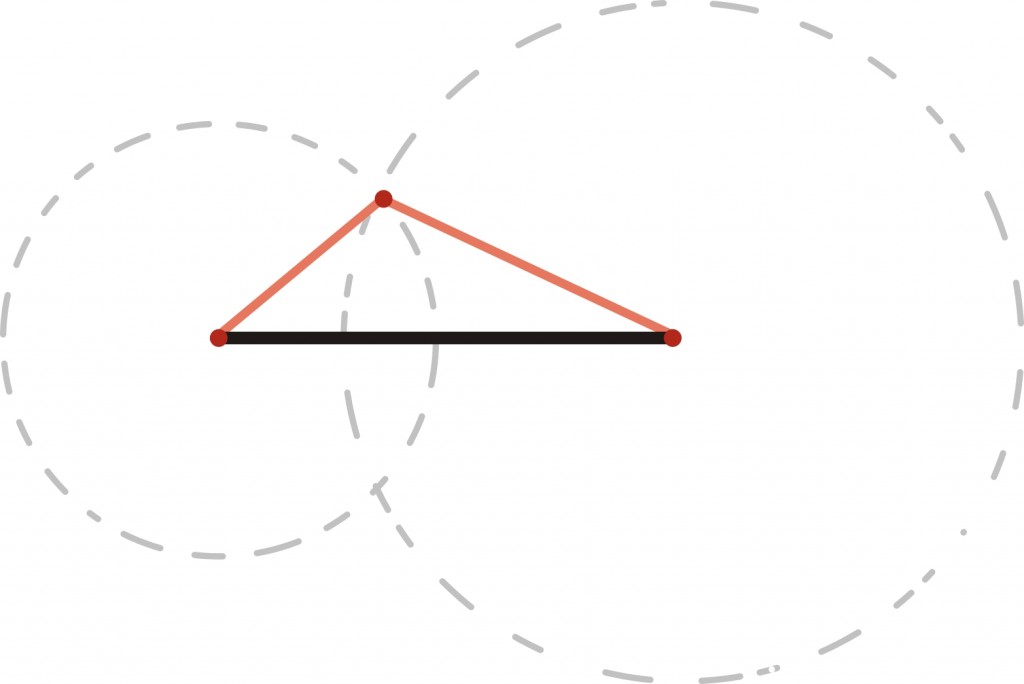
Selle tõestamine, et kolme külje võrdsusest järeldub kolmnurkade kongruentsus, siiski väga raske ei ole. Tuleb lihtsalt märgata, et sirkli ja joonlaua abil võib kolme külge teades konstrueerida täpselt ühe kindla kolmnurga.
Esmalt võtame suvaliselt ühe kolmest küljest ja paigutame selle joonisele. Järgnevalt tahaksime selle külje otspunktidesse paigutada teised kaks nii külge, et nad lõikuksid. Selle jaoks kirjeldame mõlema külje jaoks sirkliga kõik tema võimalikud otspunktid: saame kaks ringjoont. Need ringjooned lõikuvad kahes punktis ja seega saame kaks võimalikku kolmnurka. Õnneks on aga ülemine ja alumine pool sümmeetrilised ning mõlemad võimalused annavad sama tulemuse: üheainsa võimaliku kolmnurga.
Tegelikult jagub kolmnurkade kongruentsuse garanteerimiseks veel teisigi tingimusi: piisab sellest, kui näiteks kaks külge ja nendevaheline nurk on võrdsed, või isegi sellest, kui kolmnurga kõik kõrgused on võrdsed. Kõik need tingimused põhinevad trigonomeetrilistel seostel.
Sarnased kolmnurgad
Käesolevas peatükis huvitab meid aga eelkõige see, millal on kolmnurgad „sama kujuga” ehk millal võib neid suurendamise ja vähendamise teel kongruentseteks muuta. Selliseid kolmnurki nimetatakse sarnasteks kolmnurkadeks.
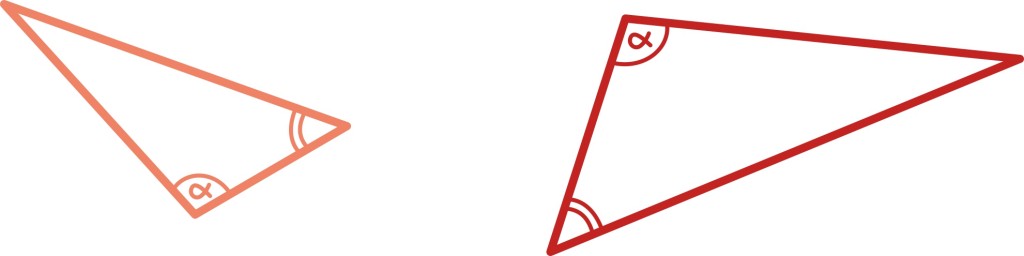
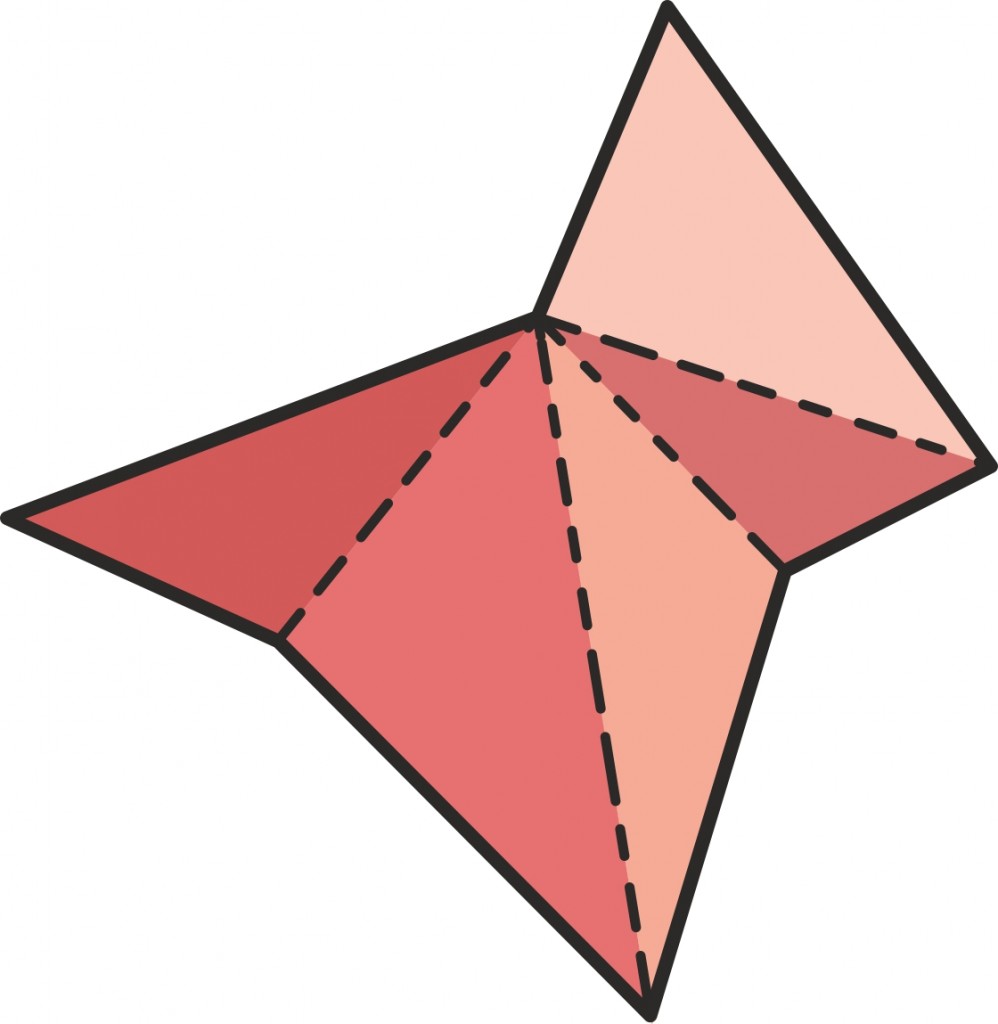
Esimese joonise hoolikam silmitsemine vihjab, et ilmselt piisab „sama kuju” garanteerimiseks juba ainuüksi nurkade võrdsusest. Tõepoolest, järgnev joonis peaks seda tõest fakti veelgi veenvamalt esitama:
Kasulik on märgata, et kuna kolmnurga nurkade summa on 180 kraadi, piisab kolmnurga kõikide nurkade kindlaks määramiseks tegelikult ainult kahe nurga teadmisest.
Kuidas on omavahel seotud sarnaste kolmnurkade küljed?
Nagu mainisime, võib sarnaseid kolmnurki suurendamise ja vähendamise teel võrdseteks muuta ning võrdsetel kolmnurkadel on muidugi võrdsed küljed.
Geomeetriliste kujundite suurendamisest ja vähendamisest võib aga mõelda lihtsalt kui kõikide pikkuste läbikorrutamisest positiivse reaalarvuga, jättes nende paiknemise samaks. Näiteks kui suurendame kolmnurka kaks korda, korrutame kõik küljepikkused läbi kahega.
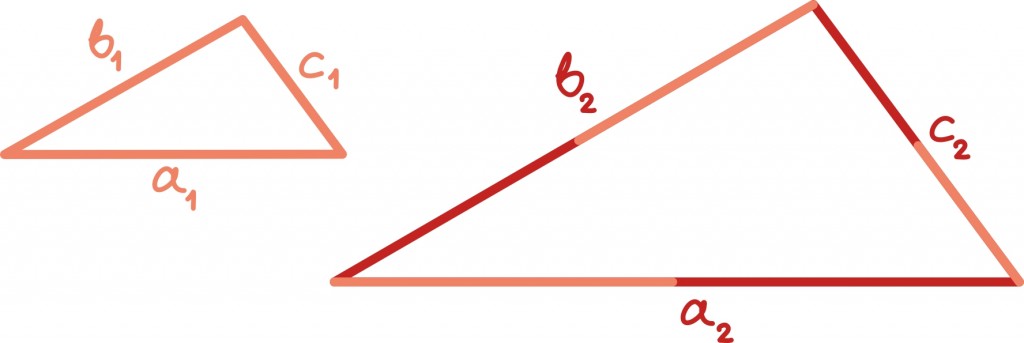
Seega teame, et kui kolmnurgad on sarnased, siis ühe kolmnurga külgede pikkustest a1, b1, c1 saab teise kolmnurga küljepikkused a2, b2, c2, kui korrutada neid sama reaalarvuga. Teisisõnu küljepikkused on proportsionaalsed ehk võrdelised:
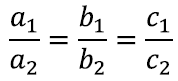
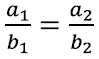
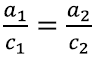
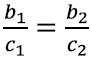
Täisnurkne kolmnurk ja trigonomeetrilised põhiseosed
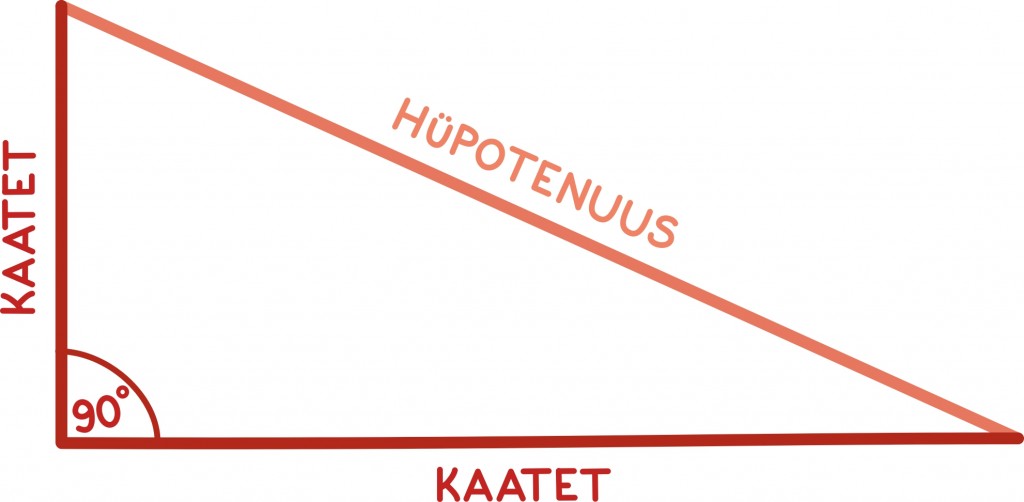
Tuletame meelde, et täisnurkseks kolmnurgaks nimetatakse kolmnurka, mille üks nurk on 90 kraadi. Täisnurkse kolmnurga külgedel on erilised nimetused: 90-kraadilise nurga lähiskülgi nimetatakse kaatetiteks ning vastaskülge hüpotenuusiks.
Nagu mainisime on „sama kujuga” kolmnurkades võrdsed kõik nurgad ning ka üksteisele vastavate nurkade lähiskülgede suhted.
Kui teame lisaks, et kolmnurk on täisnurkne, siis piisab kõikide nurkade määramiseks veel ainult ühe nurga teadmisest – on ju sel juhul üks nurk 90 kraadi, teist nurka teame ja kolmanda nurga võime välja arvutada, kuna kõige kolme nurga summa on 180 kraadi.
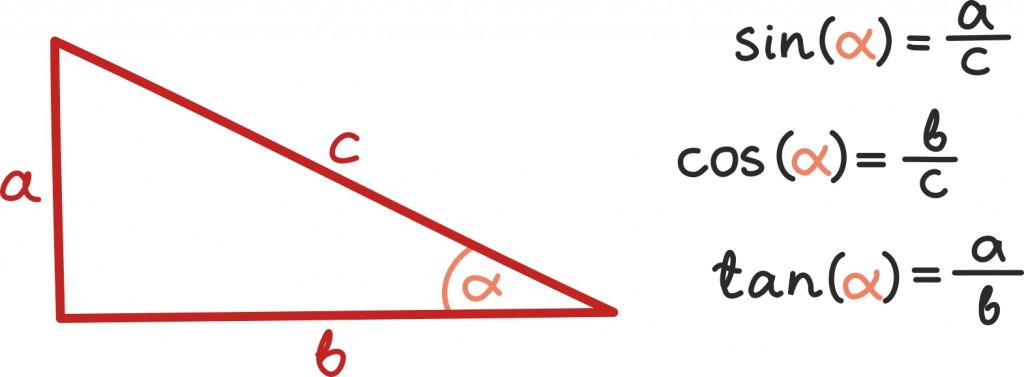
Ehk teisisõnu, kui meile on antud üks kindel teravnurk (miks just teravnurk?), mille tähistame kokkuleppeliselt kreeka tähestiku esimese tähega α, siis teame, millise kujuga on meie kolmnurk ning saame kindlaks määrata ka külgedevahelised suhted:
- nurga α vastaskaateti pikkus jagatud hüpotenuusi pikkusega
- nurga α lähiskaateti pikkus jagatud hüpotenuusi pikkusega
- nurga α vastaskaateti pikkus jagatud lähiskaateti pikkusega
Kõik kolm suhet annavad vastuseks ühe arvu. Kuna need arvud sõltuvad üheselt ainult valitud nurgast α, on tegemist funktsioonidega [lk 64] nurgaväärtusest.
Näiteks kui α = 45º, siis on ka teine teravnurk 45º ning seega kolmnurk võrdhaarne. Kaatetitevaheline suhe on seega täpselt 1.
Leitud funktsioonid on käibel nii tihedasti, et neile on mõistlik anda lühemad nimetused:
- vastaskaateti ja hüpotenuusi suhet kutsutakse siinuseks nurgast α,
- lähiskaateti ja hüpotenuusi suhet kutsutakse koosinuseks nurgast α,
- vastaskaateti ja lähiskaateti suhet nimetatakse tangensiks nurgast α.
Neid kolme funktsiooni kokku kutsutakse trigonomeetrilisteks funktsioonideks ning otse definitsioonist võib märgata seost nende vahel: tangens on võrdne siinuse ja koosinuse jagatisega.
Nende vanamoodsate nimetuste jaoks on matemaatiliselt kasutusel veel järgnevad lühendid:
Eelneva tulemuse, kus 45-kraadise nurga puhul on kaatetitevaheline suhe täpselt 1, saaksime nüüd kirja panna järgnevalt:
Olgugi et nende funktsioonide väärtused ise on leitud külgedevaheliste suhete kaudu ühes nurga poolt kindlaks määratud täisnurkses kolmnurgas, siis ei pea funktsiooni ennast sugugi rakendama ainult täisnurkse kolmnurga nurkadele. Trigonomeetrilisi funktsioone võib vabalt rakendada ka nurgaväärtustele, mis pärinevad viisnurgast, lihtsalt kahe haara vahelt või mujaltki.
Tõsi küll, praegu nõuame endiselt, et kasutatav nurgaväärtus oleks teravnurkne ehk väiksem kui 90 kraadi, sest oskame ainult sel juhul külgedevahelisi suhteid leida ja seega trigonomeetrilisi funktsioone defineerida. Kohe vabaneme aga sellestki ettekirjutusest, alustades üsna loomulikust küsimusest.
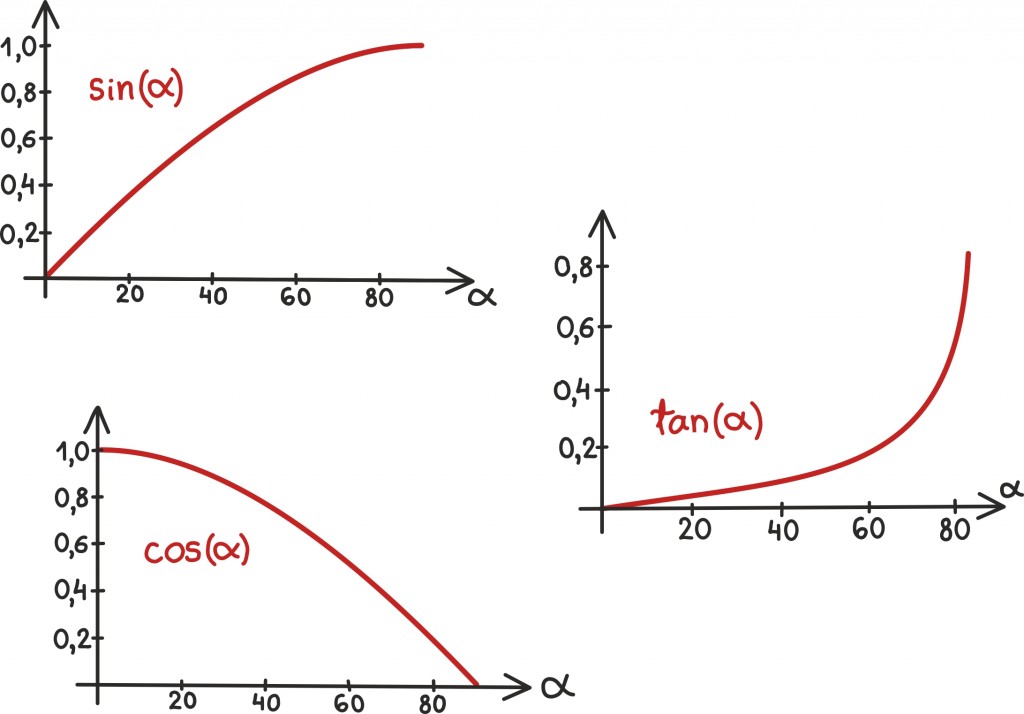
Kuidas trigonomeetrilised funktsioonid välja näevad?
Sellele küsimusele vastamiseks peame lihtsalt joonistama kolmnurki erinevate nurga α väärtustega.
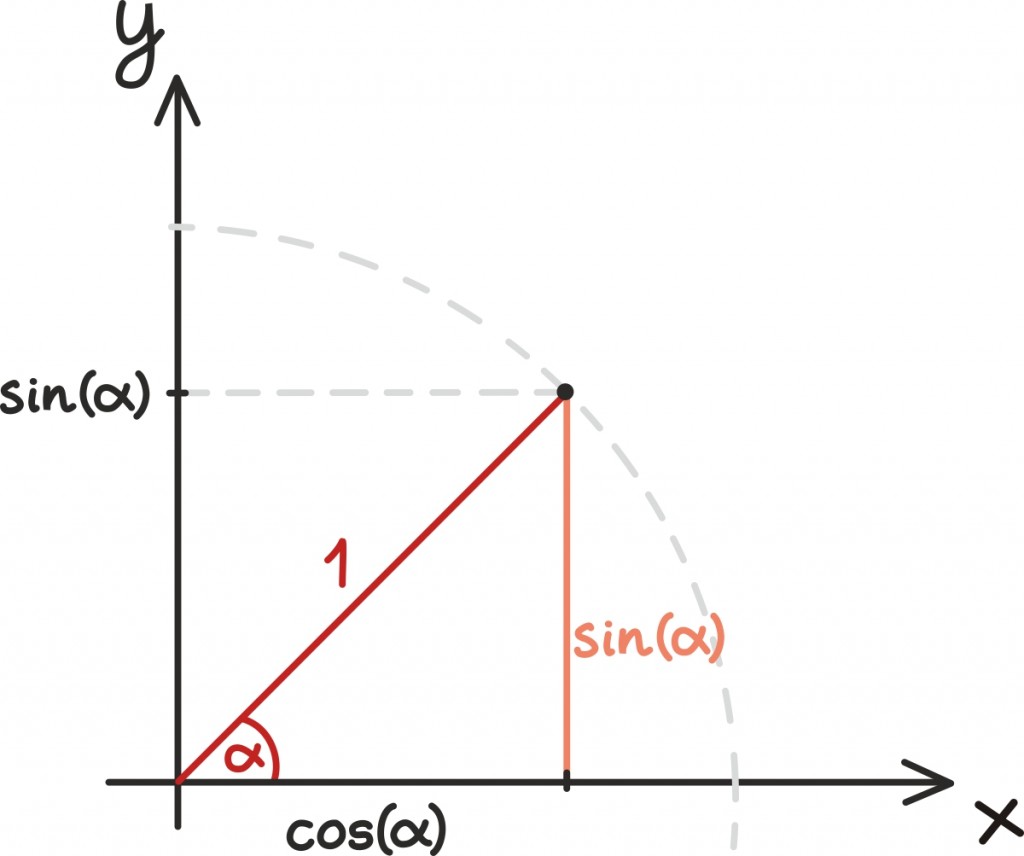
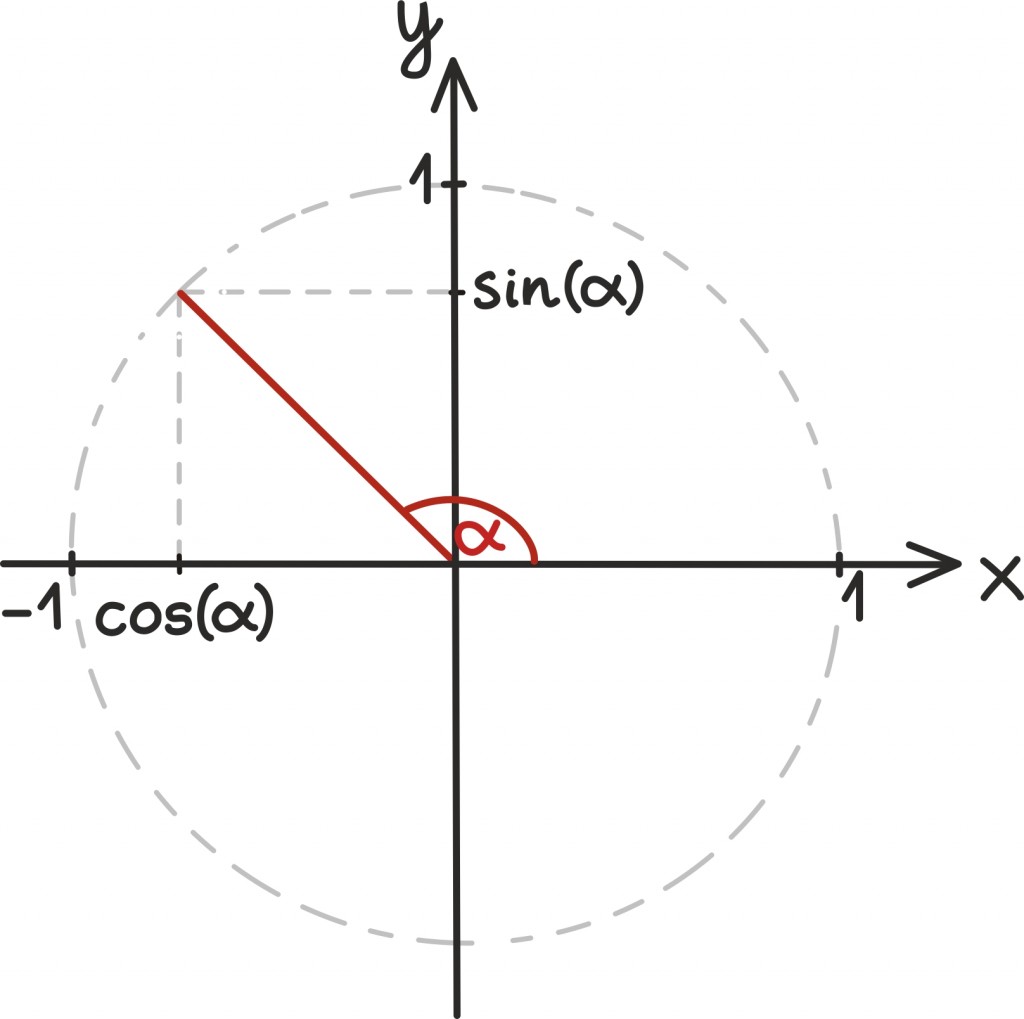
Kolmnurga suuruse võime muidugi ise valida. Kaval on valida kolmnurga suurus nii, et hüpotenuusi pikkuseks on üks. Sel juhul on nurga siinus võrdne täpselt vastaskaateti pikkusega ning nurga koosinus võrdne lähiskaateti pikkusega.
Seame nüüd ühe kolmnurga tipu koordinaatteljestiku nullpunkti ning joonistame sinna hüpotenuusi pikkusega üks. Kaatetiteks jäävad hüpotenuusi otsastx-teljele viiv lõik ja ka lõik, mis sealt tagasi nullpunkti jõuab.
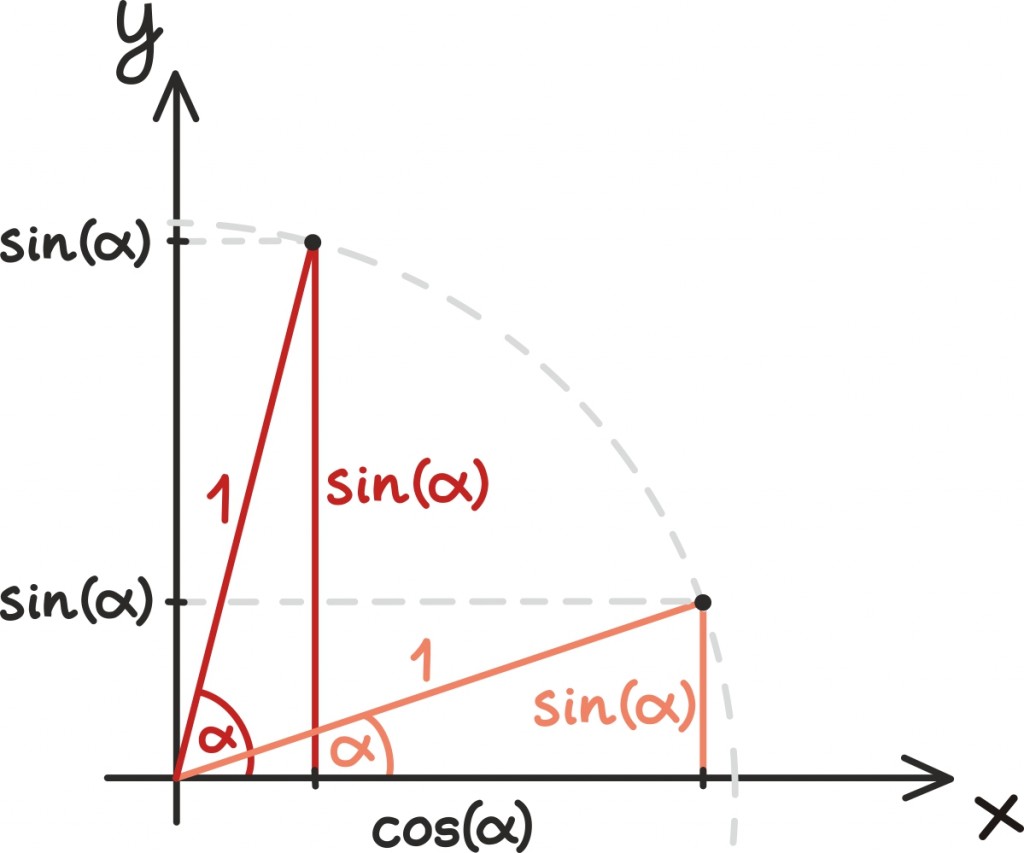
Nüüd, siinus mingist nurgast on vastaskaateti jahüpotenuusi pikkuste suhe. Kuna hüpotenuus on üks, siis siinus ongi siin võrdne vastaskaateti pikkusega. Joonisel on näha, kuidas siinuse väärtus kasvab koos nurga väärtusega.
Vastaskaateti pikkuse annab aga täpselt haara ja ringjoone lõikepunkti y-koordinaat. Koosinuse annab samas raamistikus selle lõikepunkti x-koordinaat ning tangensi y– ja x-koordinaadi suhe. Seda viimast võime tõlgendada veel lihtsamaltki: tangens näitab haara poolt määratud sirge tõusu. Kui jagame y-koordinaadix-koordinaadiga, siis saame teada, kui palju haara määratud sirge iga ühiku kohta tõuseb.
Edasi on lihtne panna arvuti, mõni sõber või sõbranna siinuse, koosinuse ja tangensi graafikuid joonistama:
Märkame aga, et meie nüüdses konstruktsioonis ei ole küll midagi teravnurkade jaoks spetsiifilist. Leidsime nurga siinuse, koosinuse ja tangensi lihtsalt kui nurgahaara ja ühikringjoone lõikepunkti koordinaadid. See nurga haar võib ju aga x-teljega jätta ükskõik millise nurga, mitte ainult teravnurga. Nii saamegi defineerida trigonomeetrilised funktsioonid suvalise nurgaväärtuse, näiteks 2013 kraadi jaoks.
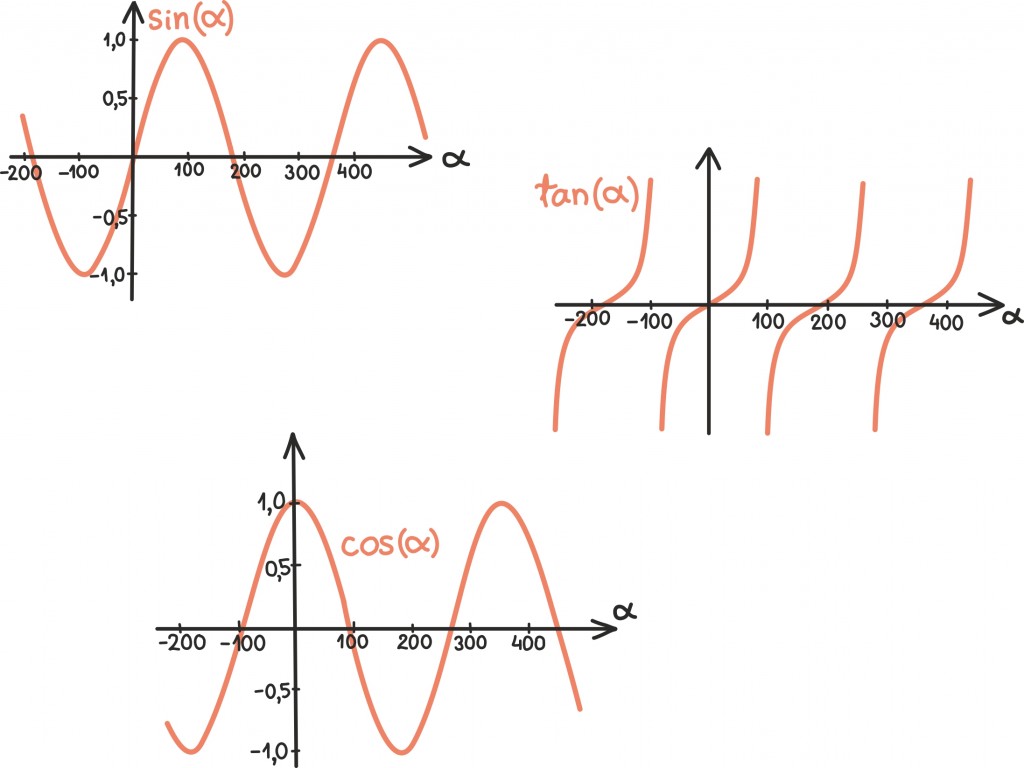
Trigonomeetrilised funktsioonid näevad oma täies pikkuses välja järgmised:
Esiteks võib märgata, et trigonomeetrilised funktsioonid on ilusasti perioodilised ehk teisisõnu nende kuju on mööda x-telge edasi liikudes korduv. See tuleneb muidugi otseselt definitsioonist – nurgad, mis erinevad täispöörde võrra, paiknevad ju x-telje suhtes täpselt ühte moodi ning seega annavad ka täpselt sama siinuse, koosinuse, tangensi. Trigonomeetrilistest funktsioonidest ja perioodilisusest räägime aga pikemalt juba teises alapeatükis [lk 230].
Teise asjana ehmatab muidugi ära tangensi katkevus iga poolringi ehk iga 180 kraadi järel. Seejuures esimene katkemine on juba 90 kraadi juures. Selles ei ole siiski midagi ehmatavat – see juhtub ju lihtsalt sellepärast, et neis kohtades on koosinus võrdne nulliga ning kuna nulliga jagada ei saa, ei saa ka tangensile väärtust leida.
Sellest murest võib mõelda ka sirge tõusu raames: sirgele, mis on vertikaalne ehk y-teljega paralleelne, ei oskagi ju tõusu vastavusse seada. Tõuseb ta lõpmatult kiiresti ülespoole või allapoole?
Trigonomeetriliste funktsioonide pöördfunktsioonid
Mitmel pool õpikus tulevad esile pöördfunktsioonid. Lühidalt rääkisime neist juba funktsioonide peatükis [lk 68], kus täheldasime, et pöördfunktsioonid rahuldavad järgmist seost:
Teisisõnu, ühe funktsiooni pöördfunktsioon nullistab täpselt tema efekti ning annab tagasi algse väärtuse.
Näiteks võiks öelda, et kolme liitmise pöördfunktsioon on kolme lahutamine. Hiljem näeme, et eksponentsiaalfunktsiooni pöördfunktsioon on logaritmfunktsioon [lk 290], ning et tuletis ja integraalgi on teineteise pöördoperatsioonid [lk 352].
Trigonomeetria kontekstis mõtleme pöördfunktsiooni all üsna lihtsat küsimust: kui enne leidsime nurga abil tema siinuse või koosinuse või tangensi, siis nüüd tahaksime ette antud väärtuse abil leida, mis nurga siinus, koosinus või tangens ta parasjagu on.
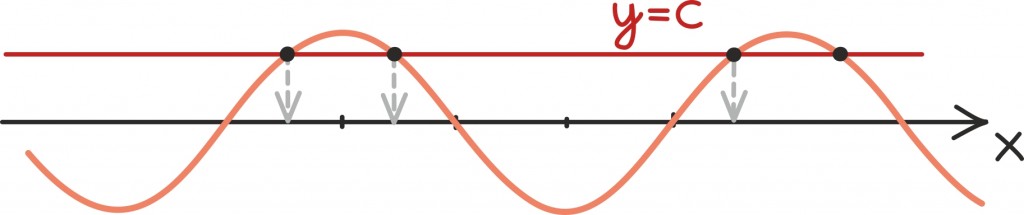
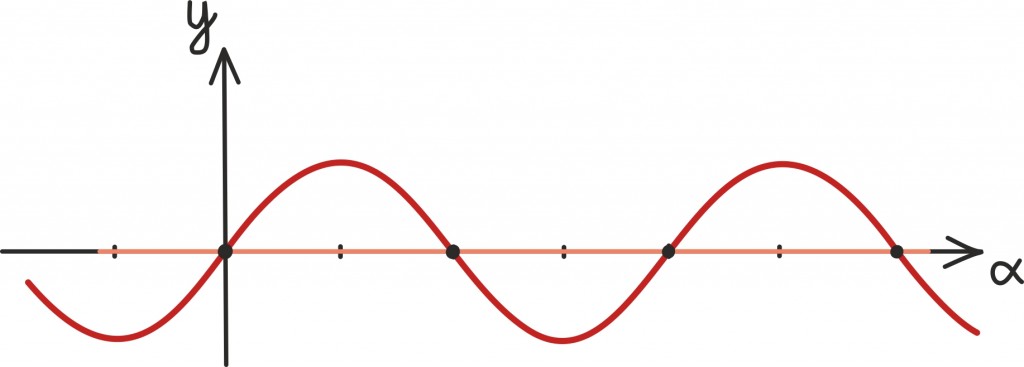
Graafiliselt tähendab see järgmist: joonistame oma trigonomeetrilise funktsiooni graafiku, valime mingi väärtuse c ning siis küsime, kus kohas funktsiooni graafik lõikab sirget y = c .
Näiteks kui teaksime, et siinus annab väärtuseks nulli, läheksime tema graafiku juurde ja vaataksime, kus ta lõikab x-telge. Vastuseks saaksime, et nurk võiks olla 0 kraadi või 180 kraadi või mõni teine 180 kraadi kordne.
Arkussiinus ja arkuskoosinus
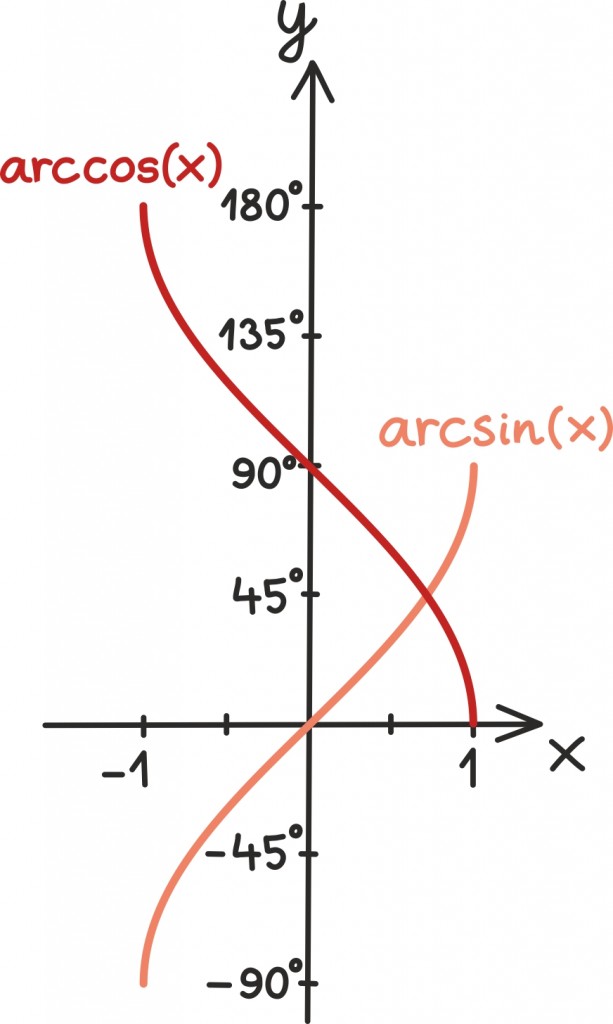
Nagu graafikult näeme, siis siinus- ning koosinusfunktsiooni jaoks neid lõikepunkte alati ei leidugi. Nimelt kui |c| > 1, on sirge y = c funktsiooni graafikust täienisti ülal- või allpool. Kõikidel teistel juhtudel on aga lõikepunkte lõpmatult palju.
See tähendab, et pöördfunktsiooni defineerimisel peame olema üsna ettevaatlikud. Esiteks saame pöördfunktsioonile väärtuse anda ainult vahemikus [–1; 1], mis siis on tema nii-öelda määramispiirkonnaks. Teiseks tuletame meelde, et funktsioon saab võtta täpselt ühe väärtuse – seega peame iga sirge jaoks kuidagi välja valima just ühe lõikepunkti.
Üks võimalus selle tegemiseks on lihtsalt nõuda, et vastus oleks mingis kindlas vahemikus – jooniselt näeme, et siinusfunktsioon võtab kõik oma võimalikud väärtused vahemikus [–90º; 90º] ning koosinusfunktsioon näiteks vahemikus [0; 180º]. Nendes piirkondades on funktsioonid üksühesed [lk 68] ning võime kohe defineerida ka pöördfunktsioonid.
Nii ongi enamasti defineeritud arkussiinus, mida tähistatakse tihti arcsin(x), kui funktsioon, mis on siinuse pöördfunktsioon vahemikus [–90º; 90º] ehk siis rahuldab selles vahemikus seost arcsin(sin(x)) =x.
Sarnaselt on siis defineeritud ka arkuskoosinus ehk arccos(x), ainult vahemikuna on kasutuses [0; 180º].
Olenevalt eesmärgist võib mõnikord kasutada muidugi ka mõnda muud vahemikku. Veelgi enam, vahepeal tahaksime kõiki vastuseid korraga esitada. Siis kirjutame umbes nii:
Sel juhul ei ole meil küll rangelt enam funktsioon, vaid loetleme lihtsalt kõik sirge y = 0 ning siinusfunktsiooni lõikepunktid ja neid on palju!
Arkustangens
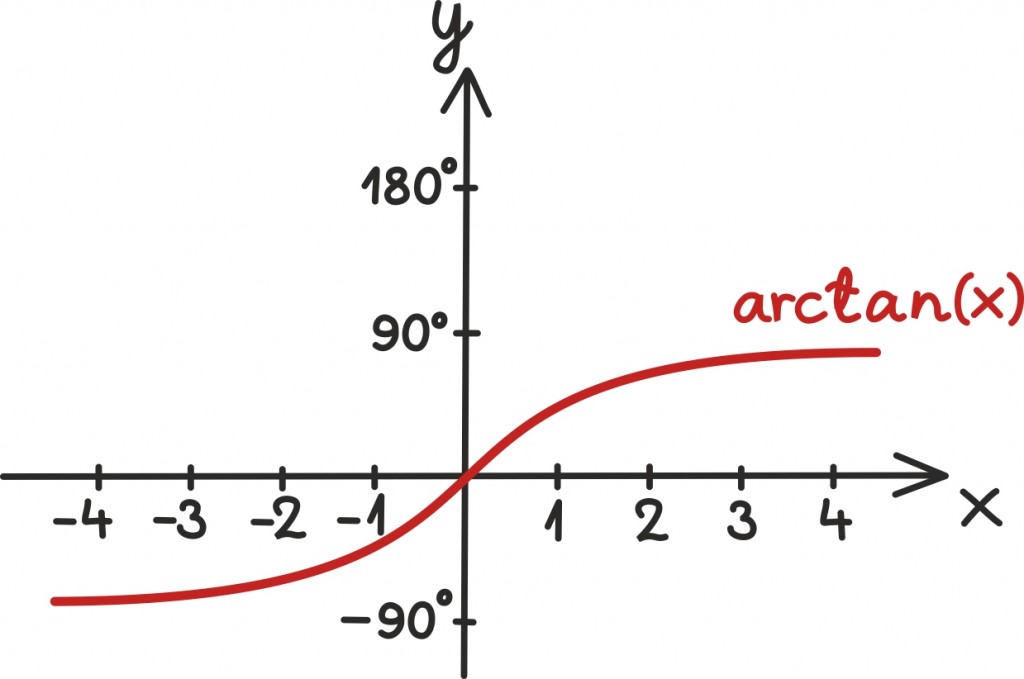
Tangensiga on selles suhtes lihtsam lugu, et ta võib võtta kõiki reaalarvulisi väärtusi. Seega on tangensi pöördfunktsiooni ehk arkustangensi määramispiirkonnaks kogu reaaltelg.
Probleem, et tangensfunktsioon on mitmes kohas sama väärtusega, muidugi säilib. Seega tuleb ka arkustangensi kui funktsiooni määramiseks välja valida üks kindel piirkond. Mõistlik valik on näiteks (–90º; 90º), aga sobiks ka mõni teine.
Arkustangensit tähistatakse arctan(x).
Tähistustest
Nobeli auhinna võitjale füüsik Richard Feynmanile ei meeldinud trigonomeetriliste funktsioonide tähistused sugugi. Talle tundus, et sin tähendab kolme arvu s, i ja n kokkukorrutamist. Veel vähem meeldis talle siinuse pöördfunktsioon, mida mõnel pool mujal tähistatakse kui sin–1(α). Õigusega tekitas see segadust, sest seda võiks tõlgendada kui
mida sellega enamasti silmas ei peeta. Igal juhul kasutas ta kooliajal siinuse ja siinuse pöördfunktsiooni järgmisi tähistusi:
Üsna varsti märkas ta siiski, et selliseid tähistusi kasutades ei saanud keegi teine tema mõtetest ja selgitustest suurt midagi aru. Seega soovitame siiski jääda tähiste sin ja arcsin juurde.
Miks just täisnurksed kolmnurgad?*
Natuke järele mõeldes võib kummitama jääma üks küsimus. Miks me seome nurki ja külgedevahelisi suhteid ikkagi just kolmnurkade kaudu ning miks just täisnurksete kolmnurkade kaudu? Kas see on lihtsalt ajalooline relikt või võib sellele ka selgitust leida?
Esimese vastusena võiks kohe öelda, et kolmnurkadest ei saa üle ega ümber. Niipea kui meil on defineeritud kaks lõigupikkust ja nendevaheline nurk, ongi meil juba kolm punkti – nurgatipp ja lõikude teised otspunktid – ja seega ka kolmnurk. Lisaks võib ju iga teise hulknurga alati kolmnurkadeks jagada.
Eelkõige on aga põhjus järgmine: kolmnurgad on ainsad hulknurgad, kus
- küljepikkuste vahelised suhted määravad üheselt ära kõik nurgad
- ning ka vastupidi, teades kõiki kolmnurga nurkasid, on määratud kõik külgedevahelised seosed.
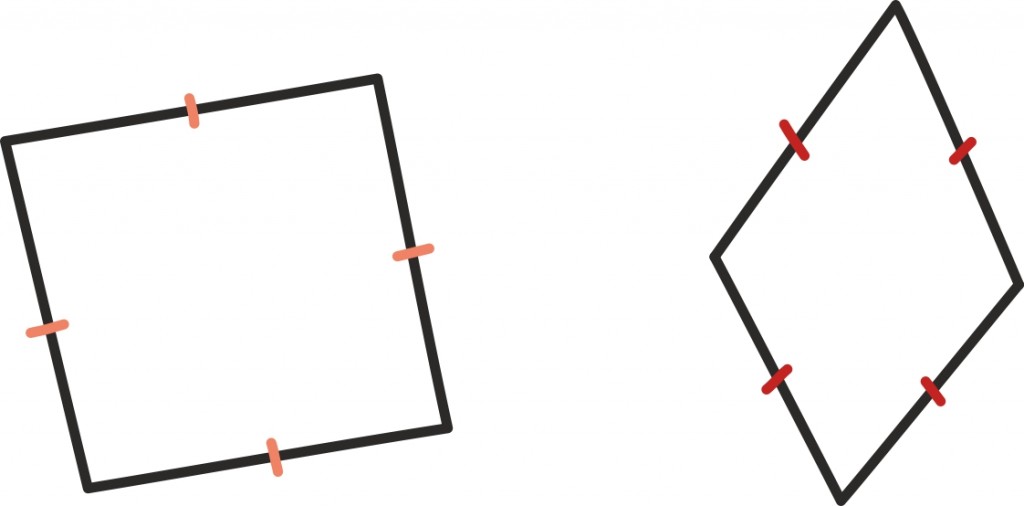
Kumbki neist seostest näiteks nelinurkade puhul enam ei kehti. Nimelt kui nelinurga neli külge on võrdsed, võivad nurgad olla endiselt erinevad: meil võib olla nii kena ruut või ka üsna lapergune romb.
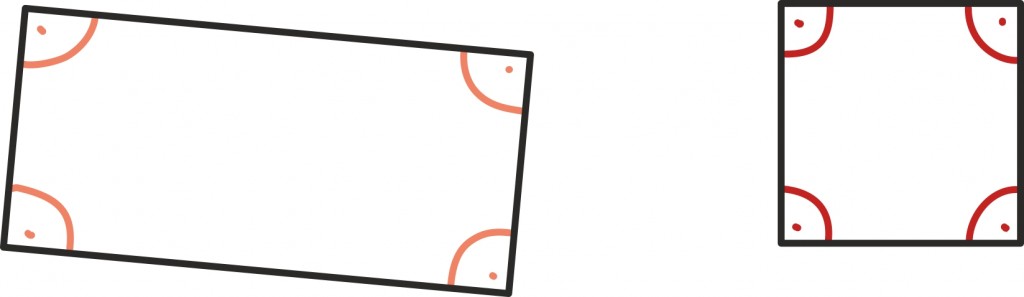
Teistpidi, teadmine, et kõik neli nurka on täisnurgad, ütleb meile vaid, et tegemist on ristkülikuga, ning muidugi leidub väga erineva külgede suhtega ristkülikuid.
Aga isegi kui lepime, et just kolmnurgad on mõeldud nurkade ja külgedevaheliste suhete sidumiseks, siis miks on kasutusel just täisnurksed kolmnurgad?
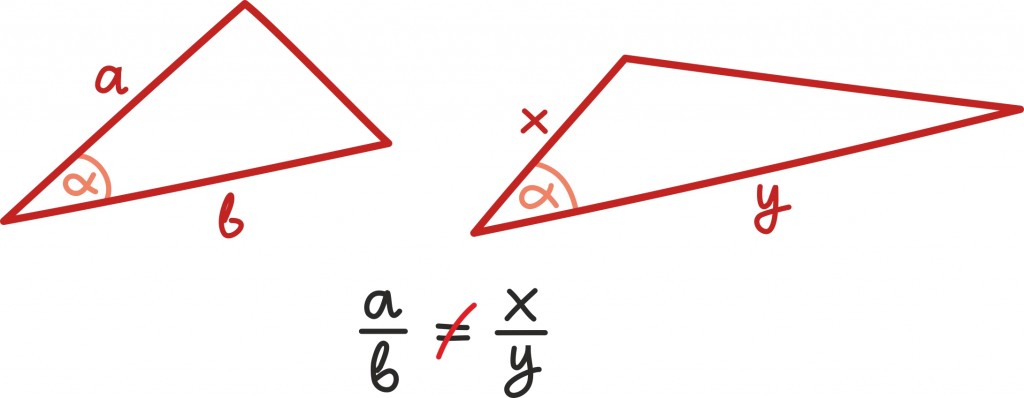
Nagu mainisime, on kolmnurga „kuju” määramiseks vaja teada vähemalt kahte nurka. Ainult ühest nurgast lähiskülgede suhte määramiseks ei piisa, sest sama nurga lähiskülgede suhe võib olla väga erinev:
Kuna teame, et iga kahe nurga teadmisest piisab kolmnurga „kuju” määramiseks, on kaval nipp üks nurk alatiseks fikseerida. Nagu eespool ka nägime, on sel juhul kolmnurga „kuju” leidmiseks vaja veel teada ainult ühte nurka ning on täiesti mõistlik rääkida selle nurga lähiskülgede vahelisest suhtest.
Fikseeritava nurga suuruse võiksime muidugi vabalt valida. Siiski, kõige paremini käsitletava, loomulikuma ja ilusama teooria saame kasutades täisnurkseid kolmnurki – ehk siis fikseerime ühe nurga täisnurgaks.
Põhjuseid selle valiku eelistamiseks on mitmeid, mõned üksikud neist on näiteks järgnevad.
- Nurk 90º on kõige sõmmeetrilisem valik – ta on täpselt poolel teel 0 kraadist 180 kraadini.
- Nagu nägime,võime sel juhul trigonomeetrilisi funktsioone defineerida lihtsalt ühikringjoone x– ning y-koordinaatide abil.
- Skalaarkorrutisel on tänu sellele valikule ilus valem vektorite pikkuste ja nendevahelise nurga koosinuse abil [lk 144].
- Iga muu kolmnurga saame jagada täisnurkseteks kolmurkadesks ja seeläbi leida ka nurkade jakülgede vahelisi seoseid – ühte neist nimetatakse siinusteoreemiks.
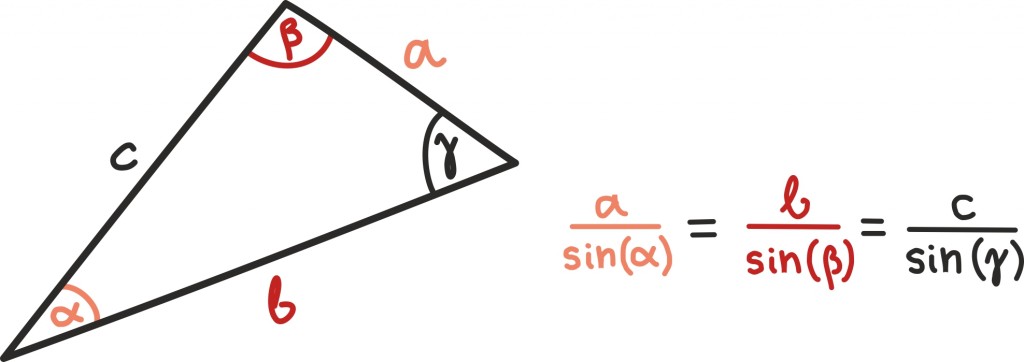
Siinusteoreem
Kasutades täisnurkse kolmnurga jaoks defineeritud trigonomeetrilisi põhiseoseid, võime omavahel siduda nurkasid ja külgi ka mittetäisnurksetes kolmnurkades.
Tuntuim selline seos on ilmselt siinusteoreem, mis väidab, et iga nurga vastaskülje ja selle nurga siinuse suhe on võrdse väärtusega. Kuigi intuitiivselt on selge, et nurgad ja külgede suhted peavad olema omavahel seotud, siis siinusteoreemi täpne sõnastus on siiski üllatavalt leidlik ja lihtne:
Enne kui siinusteoreemi tõestama asume, räägime mõnest tema matemaatilisest rakendusest.
Mõned siinusteoreemi rakendused
Esimese rakendusena aitab siinusteoreem leida puuduvaid elemente kolmnurgas – tema abil võime teadmised nurkadest pöörata teadmisteks küljepikkuste kohta ja vastupidi.
Samuti võime siinusteoreemist vähemalt teravnurkse kolmnurga jaoks üsna kergesti järeldada midagi päris ilusat: kolmnurga pikemate külgede vastas on suuremad nurgad.
Tõepoolest, siinusteoreemist teame, et
Nüüd kui küljepikkuste vahel kehtib a > b, siis peab kehtima ka sin(α) > sin(β). Samas aga nägime ennist, et teravnurksete nurkade jaoks on siinus kasvav funktsioon. Seega järeldame, et nurk α peab nurgast β suurem olema. Ehk suurema nurga vastas on ka suurem külg.
Siinusteoreemi tõestus teravnurkse kolmnurga jaoks
Lugeja võib paberi, pastaka ja natukese kritseldamisega veenduda, et siinusteoreem ei ütle täisnurkse kolmnurga jaoks midagi uut – kogu seos järeldub siinuste definitsioonist.
Mittetäisnurkse kolmnurga jaoks on siiski tegemist millegi uue ja põnevaga, mida on vaja ka tõestada, teisisõnu selgitada meile juba varasemate teadmiste abil. Miks muidu peaksime seda uskuma?
Kuidas siis argumenteerida? Tuletame meelde, et siinus on defineeritud täisnurkse kolmnurga kaudu. Seega tuleks kuidagi konstrueerida täisnurkne kolmnurk, milles neid definitsioone kasutada võiksime.
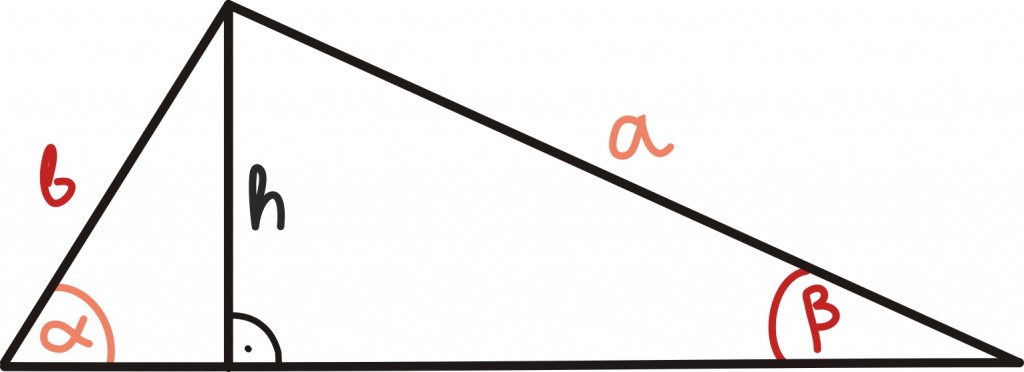
Üks võimalus on lihtsalt tõmmata kõrgus. Nii jagame algse kolmnurga kaheks täisnurkseks kolmnurgaks. See tundub juba päris hea algusena, sest nende täisnurksete kolmnurkade üks külg on ju lisaks veel võrdne – just seesama külg, mille abil saame nurga siinust välja kirjutada.
Seega kirjutamegi lihtsalt välja mõlemast kolmnurgast siinuse definitsiooni:
Avaldades mõlemast avaldisest kõrguse h, näeme, eth = b sin(α) ja samuti h = a sin(β)
Seega kehtib ka b sin(α) = a sin(β) ehk
Samamoodi võiksime muidugi ka tõmmata mõne teise kõrguse ja nii näidata kõikide suhete võrdsust.
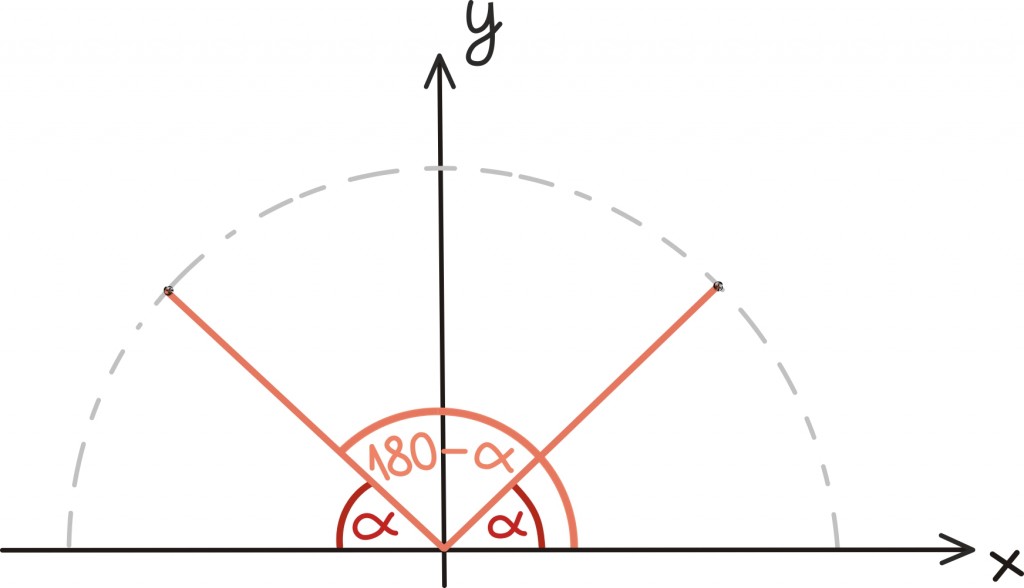
Nürinurkse kolmnurga puhul satub kõrgus küll kolmnurgast välja, aga see ei põhjusta probleeme. Nimelt kui vaadata hoolikalt siinusfunktsiooni definitsiooni suvalise nurga jaoks, näeme, et sin(α) = sin(180º – α). Tõepoolest, mõlemad haara otspunktid lõikavad ju ühikringjoont samal kõrgusel.
Siinusteoreemi laiendus
Tuleb välja, et tegelikult võib siinusteoreemi veel laiendada.
Nimelt on teada ka selle iga vastaskülje ja nurga siinuse suhte täpne väärtus – see on alati võrdne kolmnurga ümberringjoone diameetri pikkusega. Seega võime, kasutades ikka samu vanu tähiseid nurkade külgede jaoks ning tähistades kolmnurga ümberringjoone raadiuse R-iga, kirjutada siinusteoreemi täiskujul välja järgnevalt:
Sellel korral on tõestus pisut kavalam ja jätame ta huvitunutele nuputamiseks või järele pärimiseks.
Koosinusteoreem
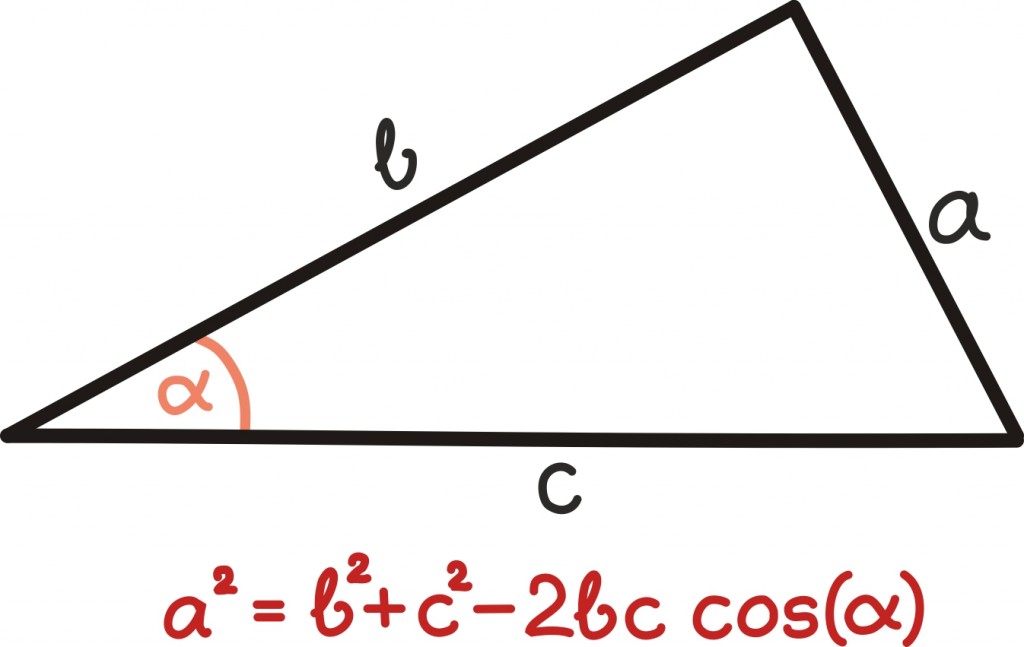
Teine tuntud trigonomeetriline seos iga kolmnurga jaoks on koosinusteoreem.
Koosinusteoreem võimaldab leida kahe küljepikkuse ning nende külgede vahelise nurga abil kolmanda külje pikkust:
Koosinusteoreemist järeldub näiteks kohe ka see, et iga kolmnurga määravad üheselt ära kaks küljepikkust ning nende külgede vaheline nurk. Tõepoolest, lähtudes neist teadmistest võime leida kolmanda külje pikkuse ja seda me juba teame, et kolme küljepikkusega on kolmnurk üheselt määratud.
Koosinusteoreem näeb juba peaaegu välja nagu Pythagorase teoreem. See visuaalne seos pole sugugi petlik. Tuletades meelde, et cos(90°) = 0 näeme, et täisnurkse kolmnurga korral väidabki koosinusteoreem täpselt sedasama, mida Pythagorase teoreemgi.
Oleks tore ka teada, kuidas koosinusteoreemi eelnevatest teadmistest järeldada. Teisisõnu on küsimus: kuidas kahe külje ja nendevahelise nurga abil leida kolmanda külje pikkus?
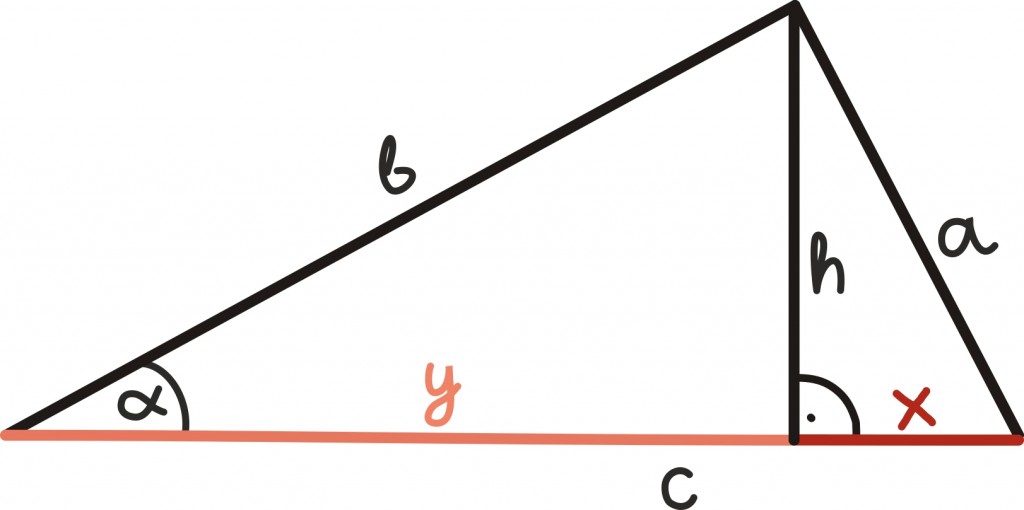
Konkreetsemalt seame siis eesmärgiks leida külje apikkus külgede b, c ja nendevahelise nurga α abil.
Üks võimalus on alustada siinusteoreemi puhul kirjeldatud viisil ning tekitada kõrguse abil täisnurkne kolmnurk. Nii seame end toredasse olukorda, kus saame kasutada koosinuse definitsiooni täisnurkses kolmnurgas ning lisaks veel koosinusteoreemi sugulast Pythagorase teoreemi.
Seega saame Pythagorase teoreemi abil kirjutada külje a pikkuse kolmnurga kõrguse h ning abilõigu x toel:
Abilõigu x pikkuse saame aga kirjutada külje c ning sama abilõigu y abil: x = c – y ja seega x2 = (c – y)2.
Võib küsida, mis sellest ikkagi kasu on, kui kirjutame abilõigu x asemele hoopis abilõigu y. Õnneks on meil ka vastus: uurides veel kord vasemal asuvat täisnurkset kolmnurka, võime välja kirjutada koosinuse definitsiooni:
Seega abilõigu y pikkuse võime esitada meile sobivate elementide abil.
Pannes kõik kokku, saame
Lihtsustame
Asendades nüüd leitud abilõigu y pikkuse y = b cos(α), saamegi koosinusteoreemi nime all välja kuulutatud seose:
Siin on ju olemas täpselt seesama liige, mis koosinusteoreemi Pythagorase teoreemist eristab! Pärast vektoritega seose loomist järeldubki kogu koosinusteoreem tegelikult ainult skalaarkorrutise omadustest.
Sisuliselt on tõestus sama kui see, mille pakkusime lisaloona Pythagorase teoreemi jaoks vektorite peatükis [lk 147], – huvitunud lugejal soovitame detailid siiski ise kokku panna.
Trigonomeetria kosmoses: robotkäsi
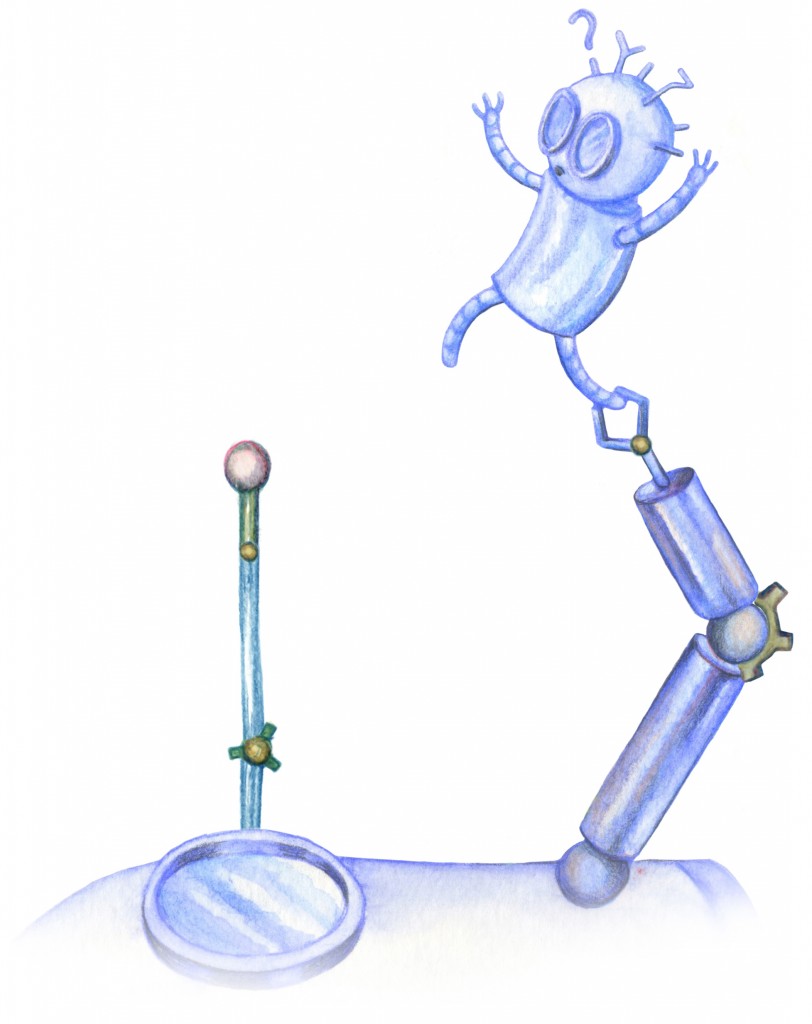
Naaseme nüüd probleemi juurde peatüki algusest: kuidas kontrollida kahe liigesega robotkätt, et ta jõuaks katkise antenni otsani?
Meenutame, et olukord oli täpselt nii hea või halb nagu pildil.
Olukorrast matemaatiliseks mõtlemiseks peame üleliigsetest detailidest lahti saama ning kõike veidi lihtsustama. Näiteks oletame, et robotkäsi liigub ainult ühel tasandil ning et see ongi just jooniseks valitud tasand. Võib ju näiteks optimistlikult mõelda, et kolmandas mõõtmes võime robotkätt niisama nihutamise teel liigutada.
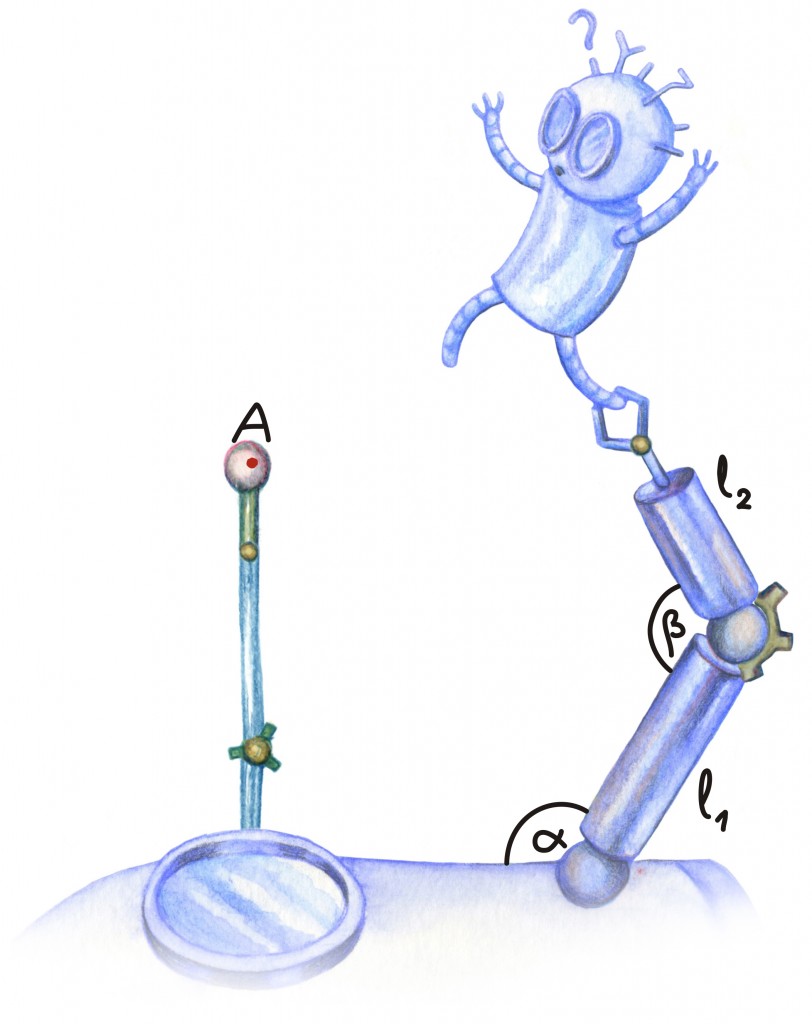
Edasi peame meile olulised elemendid kuidagi tähistama. Meile on teada robotkäe kahe hoova pikkused l1 ja l2 ning oletame, et võime mootorite abil kontrollida liigeste pöördenurkasid α ja β. Nimetame neist alumist õla- ja teist küünarliigeseks. Meie eesmärk on viia robotkäe ots (ja astronaut) etteantud punkti A, kusjuures muuta võime nurkade αja β väärtuseid.
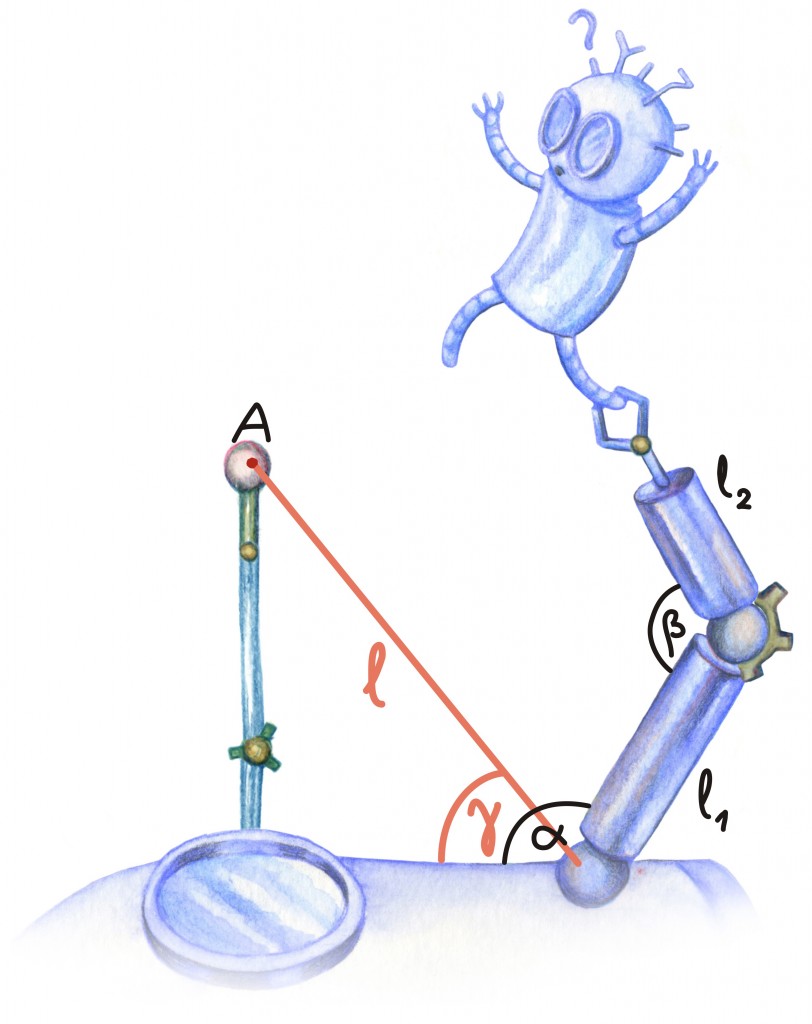
Ülesande lahendamiseks on muidugi vaja ka veel täpsustada, mida me punkti A kohta juba teame. Tundub üsna mõistlik eeldada, et teame esiteks punkti A kohta tema kaugust õlaliigesest – näiteks laserite peegeldust uurides. Teisalt võime eeldada, et teame nurka, mille jätab see kiir õlaliigesest punkti Ahorisontaalse tasandiga. Tähistame saadud kaugust näiteks l-iga ning nurka ennast γ-iga. Nii on meil lõplik joonis järgmine:
Siin võime anda oma ülesande juba üsna matemaatiliselt: eesmärk on seega leida pikkuste l, l1ja l2 ning nurga γ abil nurgad α ja β. Lahendusviisiks on meil trigonomeetria.
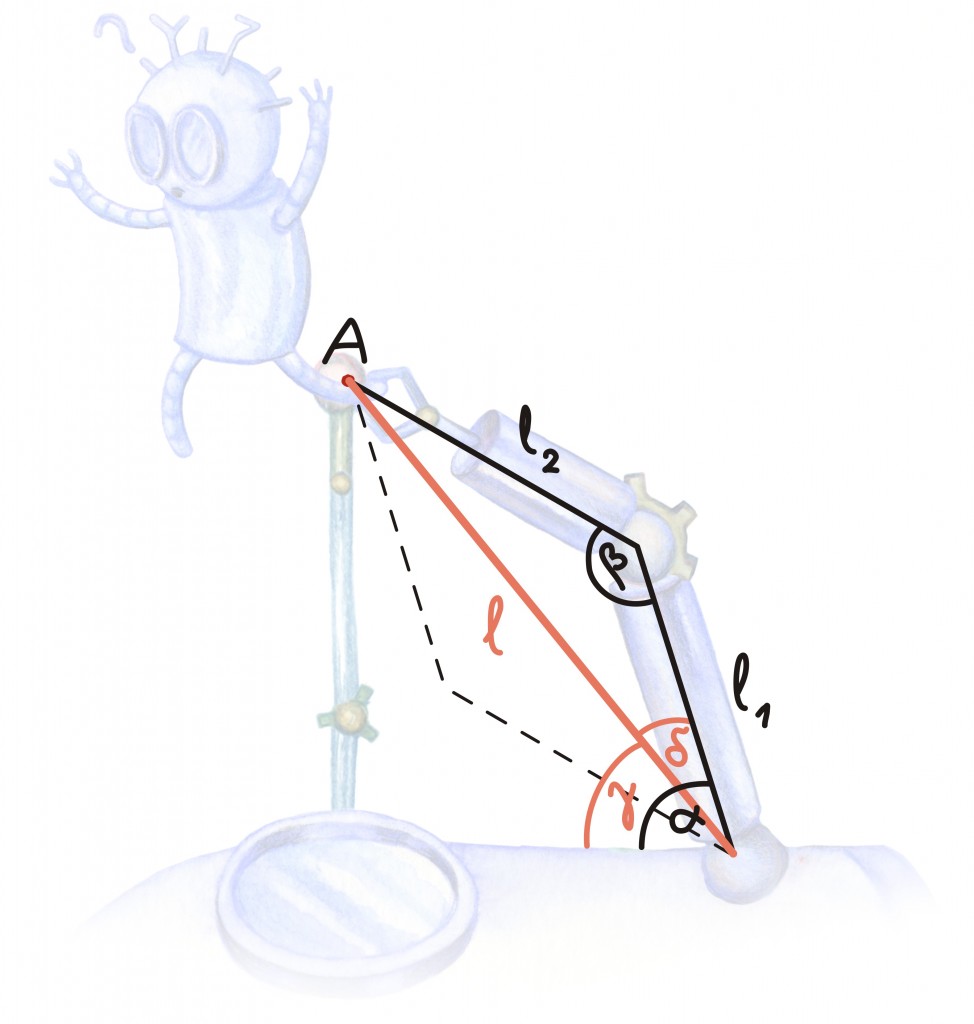
Tuletame meelde, et kolmnurga kolm küljepikkust määravad täpselt ära kolmnurga kuju ja suuruse. Kuna lisaks on veel teada kaks kolmnurga tippudest – õlaliiges ja punkt A –, jääb meil saadava kolmnurga jaoks täpselt kaks võimalust, olenevalt sellest, kuidas punktile A läheneme.
Oletame, et valime joonisel näidatud viisi. Järgmine küsimus on siis, kuidas küljepikkustest nurgad leida. Selle jaoks leiame abi juba läbitud peatükist: koosinusteoreem seob omavahel kõik kolmnurga küljed ning ühe nurga koosinuse. Nii võime leida nurga β koosinuse:
Nagu nägime pöördfunktsioonide juures, võime nurga koosinuse põhjal kergesti leida ka nurga enda väärtuse. Kõige lihtsam on küsida nurga väärtust taskuarvutilt – igal uhkemal taskuarvutil on nurga koosinuse väärtuse põhjal nurga leidmine tähistatud funktsiooniga arccos(x) või cos–1(x).Täpselt samamoodi võime leida ka nurga δ koosinuse:
ja seejärel arkuskoosinuse abil nurga δ väärtuse.
Viimaks saame nüüd ka nurga α lihtsalt välja arvutada. Olenevalt sellest, kummalt poolt läheneme, on α = γ + β või α = γ – β.
Oleme nüüd täpselt kirjeldanud arvutusi, mis tuleks teha robotkäe antennini juhtimiseks. Edasi tuleks need tehted ja kõikide andmete täpsed väärtused arvutile edasi anda ning kosmosejaam saabki korda!
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!