• Märkame, et esimese sõna valikuks on meil kolm võimalust: mulle, meeldib või matemaatika.
• Kui oleme esimese sõna valinud, jääb täpselt kaks võimalust teise sõna valikuks.
• Kui aga teinegi sõna on valitud, võime kolmanda sinna vaid lõppu visata.

Esimesel sammul oli meil 3 võimalust, teisel 2 ja kolmandal ainult 1 võimalus. Kuna kõik valikud on üksteisest sõltumatud, on võimalusi kokku täpselt 3 · 2 · 1 = 6.

Oleks meil neli sõna, ei oleks kõik moodustatavad laused ilmselt enam grammatiliselt korrektsed, ent sarnase arutelu kaudu näeksime siiski, et moodustada on võimalik 4 · 3 · 2 · 1 = 24 erinevat lauset.

Sama  mõttemustrit edasi viies näeme, et sõna n jaoks oleks lausete arv n · (n – 1) · … 3 · 2 · 1 ehk teisisõnu

Faktoriaal

Selgub, et järjestikuste arvude korrutamine on nii mõnus ja nii tihti ettetulev tegevus, et sellele tasub ka päris oma tähistus anda.

Nii tähistabki 10-faktoriaal esimese kümne positiivse täisarvu korrutist 1 · 2 · … · 10 ning n-faktoriaal seega korrutist 1 · 2 · … ·(n – 1) · n. Kuni 19. sajandini tähistati n-faktoriaali sümboliga

Varsti leidis õnneks esteetilise tunnetusega prantsuse matemaatik Christian Kramp, et tegemist ei ole teab mis kena sümboliga, ning tõi kasutusele tänapäevase tähistuse: n!.

Nagu äsja lugesime, ongi n objekti permutatsioonide arv täpselt võrdne n-faktoriaaliga ehk, kuna matemaatikud sümbolitega ei priiska:

Faktoriaali kasv*

Faktoriaali juures on muljet avaldav tema kasvukiirus. Kui hakkame järjest faktoriaali välja arvutama, oleme varsti pigis – taskuarvuti ütleb üles!

Juba 20! annab meile arvu 2 432 902 008176 640 000. Kui faktoriaali meile juba tuntud funktsioonidega võrrelda, siis faktoriaal kasvab kiiremini kui ükskõik milline polünoom [lk 266] ja isegi kiiremini kui ükskõik milline eksponentsiaalfunktsioon [lk 280].

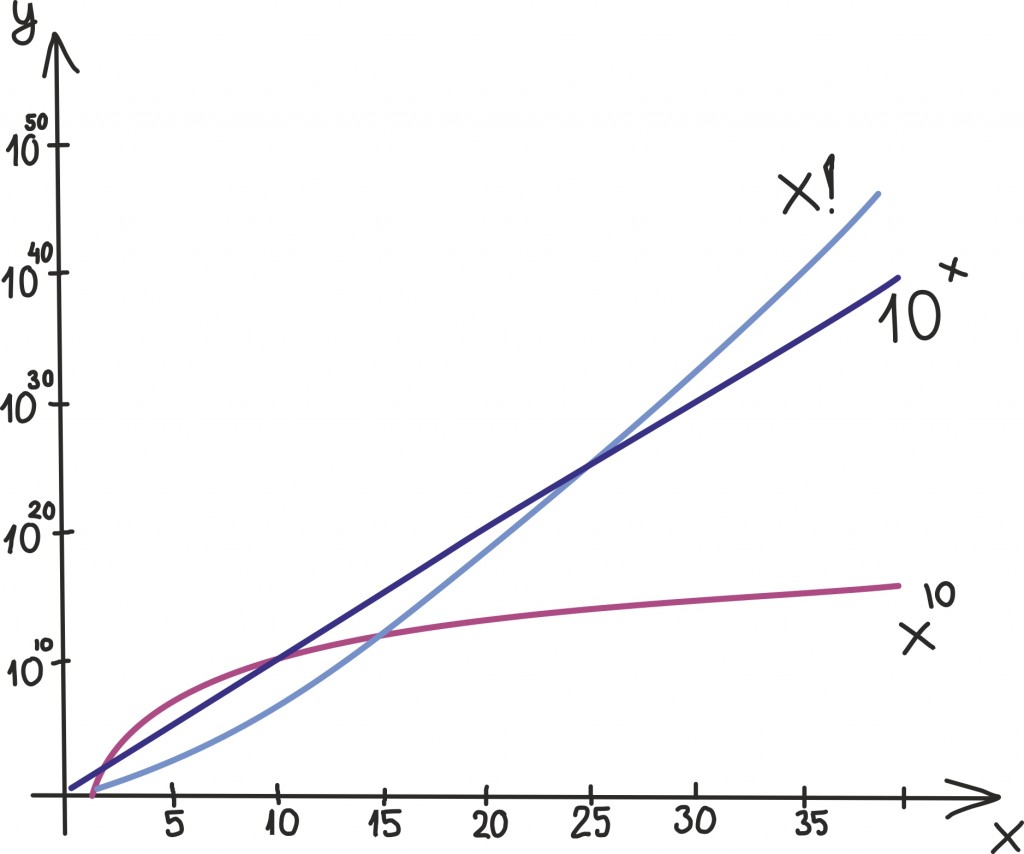
Eks lihtsaim viis ülevaate saamiseks on ikka oma silmaga mõnd näidet uurida. Jälgi, kuidas kolm erinevat funktsiooni (lilla on polünoom, tumesinine eksponentsiaalfunktsioon ning helesinine faktoriaal) kasvavad:

Faktoriaal kihutab juba üsna varakult polünoomist mööda ja veidi hiljem möödub ka eksponentsiaalfunktsioonist. Kui ainult pilt pole veel piisavalt veenev, siis võib lugeda ka järgnevat selgitust, mis küll rangele matemaatilisele täpsusele ei pretendeeri.

Märkame, et …

1. Polünoomi y = x¹⁰ kasvust võime mõelda järgmiselt: kui tema argumenti (muutuja xväärtust) 2 korda suurendame, siis funktsioon kasvab 2¹⁰ korda.
2. Eksponentsiaalfunktsiooni y = 10^x kasvust võime mõelda järgmiselt: kui tema argumenti ehk x-isuurendada 2 korda, siis on see võrdväärne funktsiooni ruutu tõstmisega.

Kumb neist kasvab kiiremini? Mõtleme juhule, kui meil on argumendiks väga suur arv, näiteks 3⁵⁰.

Selle argumendi väärtuse kahekordistamisel suureneb polünoomfunktsioon ainult 2¹⁰ korda, eksponentsiaalfunktsioon aga tervelt 3⁵⁰ korda – seega kasvab eksponentsiaalfunktsioon vähemalt selles vahemikus palju kiiremini. Kiire mõtisklus näitab, et küllap ta siis rebib varem või hiljem ette.

Aga mida tähendab faktoriaali jaoks argumendi kahekordistamine?

Arvust m! saab (2m)! ja seega argumendi 3⁵⁰ jaoks saame argumendi kahekordistamisel algse faktoriaali 3⁵⁰! asemele faktoriaali (2 · 3⁵⁰). See tähendab, et korrutame kokku 2 · 3⁵⁰ esimest naturaalarvu.

Seega faktoriaal kasvab täpselt

korda. See arv on aga palju suurem kui 3⁵⁰ – meil on kokku 3⁵⁰ tegurit, millest iga on suurem kui 3⁵⁰!. Teisisõnu, argumendi kahekordistamisel suureneb faktoriaal veel mitu korda rohkem kui ruutuvõtmise korral. Jällegi, varem või hiljem rebib ta ka eksponentsiaalfunktsioonist ette.

Niisiis peaks olema täiesti usutav, et faktoriaal kasvab kiiremini kui eksponentsiaalfunktsioon ja seega ka kiiremini kui polünomiaalfunktsioon.

Järelikult kui keegi räägib oma varade eksponentsiaalsest kasvust, tuleb muidugi üle kelkida ja vastata: see pole veel midagi, minu varandus kasvab faktoriaalselt!