Nähtuste mudelid: tabel, graafik, valem
Nähtused on aineliste objektidega toimuvad muutused. Füüsikalist nähtust kirjeldab nähtuse mudel, mida esitatakse kas tabeli, graafiku või valemina.
Tabel koostatakse selliselt, et tema abil on võimalik näha vastavust füüsikaliste suuruste üksikute väärtuste vahel.
Graafik esitleb korraga kõiki mõõteväärtusi ning kirjeldab suuruste omavahelist sõltuvust tervikuna. Kahe füüsikalise suuruse omavahelise sõltuvuse kui põhjusliku seose korral esineb üks (vabamuutuja) põhjusena, teine (seotud muutuja) aga tagajärjena. Matemaatikas nimetatakse neid vastavalt argumendiks (x) ja funktsiooniks [f(x)]. Graafiku joonestamisel kantakse põhjus (vabamuutuja, argument) horisontaalteljele (abtsiss) ja tagajärg (seotud muutuja, funktsioon) vertikaalteljele.
Valem kirjeldab füüsikaliste suuruste sõltuvust mitte ainult ühe konkreetse objekti vaid kõigi samalaadsete objektide uurimisel.
Sulle võivad huvi pakkuda need õppematerjalid:
Ruutvõrrand
Õpime tähti. Ä-täht.
Ratsionaalavaldised
Kuidas ja miks saada Ameerika presidendiks?
Numbrilised seosed
Toivo Niiberg. Õpetaja positiivne enesekehtestamine lapsevanemaga
Jäätmed pole kõigest prügi
Õpime tähti. V-täht
Urme Raadik ja Sille Jõgeva. Omavahelised suhted
Õpime tähti. A-täht
Harjuta eesti keelt A2-B1. Mängi ja nuputa
Õpime tähti. J-täht
Reesi Kuslap ja Kristiine Kurema. Kuidas õhinaga õpetada ehk mismoodi innustada õpilasi õppima?
Eesti keele grammatika kordamine 8. klassile
Täis- ja kaashäälikuühend
Häälikute pikkused
Ruutvõrrandi abil lahenduvad tekstülesanded
Sagedaimad sõltuvused kahe füüsikalise suuruse vahel on väljendatavad (mõne) astmefunktsioonina. Kõige levinumad gümnaasiumikursuses esinevad sõltuvused on:
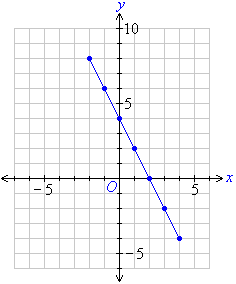
(1) võrdeline ehk lineaarne sõltuvus, kus vabamuutuja on avaldises astmes +1 => y=ax – näiteks ühtlasel liikumisel on keha poolt läbitud teepikkus on võrdeline liikumisajaga s = vt, kus s – teepikkus, v – kiirus ja t – aeg => võrdelise sõltuvuse graafikuks on sirgjoon;
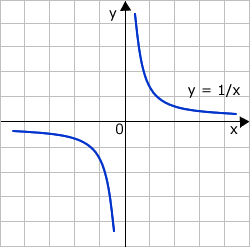
(2) pöördvõrdeline ehk retsiprookne sõltuvus, kus vabamuutuja on avaldises astmes -1 => y=ax-1 – näiteks pinnale avaldatav rõhk on pöördvõrdeline pinnaga, millele jõud mõjub p = FS-1=F/S, kus p – rõhk, F – jõud ja S – pindala => pöördvõrdelise sõltuvuse graafikuks on hüperbool;
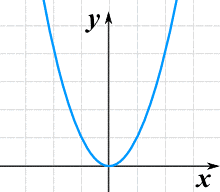
(3) ruutvõrdeline sõltuvus, kus vabamuutuja on avaldises astmes +2 => y=ax2 – näiteks keha kineetiline energia on ruutvõrdeline keha kiirusega: ![]() , kus Ek – kineetiline energia, m – keha mass ja v – keha kiirus => ruutvõrdelise sõltuvuse graafikuks on parabool;
, kus Ek – kineetiline energia, m – keha mass ja v – keha kiirus => ruutvõrdelise sõltuvuse graafikuks on parabool;
(4) pöördruutvõrdeline sõltuvus, kus vabamuutuja on avaldises astmes -2 => y=ax-2 – näiteks kehade vahel mõjuv gravitatsioonijõud on pöördruutvõrdeline kehade vahelise kaugusega: ![]() , kus F – gravitatsioonijõud, m1 ja m2 – kehade massid ja r – kehade vaheline kaugus; G – gravitatsioonikonstant;
, kus F – gravitatsioonijõud, m1 ja m2 – kehade massid ja r – kehade vaheline kaugus; G – gravitatsioonikonstant;
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!