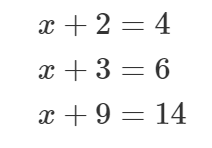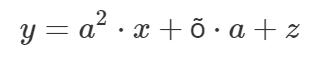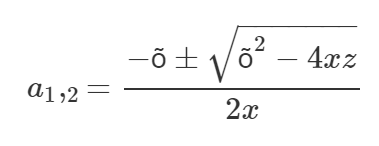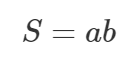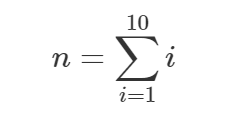Muutuja erinevates rollides  

Muutujaid kasutatakse väga erinevates rollides. Tegemist on üsna üldise ja tihti lihtsustamise eesmärgil sisse toodud mõistega. Kuidas ja mis suhtes muutuja täpselt muutub, sõltub konkreetsest kontekstist ning mõnikord kutsutakse teda hoopis mõne teise nimega.

Muutuja, võrdused ja võrrandid

Muutujaid võib kohata võrduste ja võrranditega tegeledes. Kusjuures võrrandis on lihtsalt meile veel tundmatu suurus seotud teiste, meile hästi teadaolevate suurustega. Näiteks

kohta võib sõbrale öelda, et tegemist on võrrandiga muutuja x suhtes või võrdusega juhul, kui muutuja xväärtuseks on 3.

Muutuja on võrrandite kontekstis meie otsitav objekt – selline arv, millele kahte liites saame viie. Tema väärtus on meile alguses teadmata ja nii võikski teda nimetada ka „tundmatuks”.

Keerulisemate, nii-öelda üldkujus võrrandite korral aitab muutuja kui objekti sissetoomine vältida segadust.

Üldkujus võrrand on näiteks

Kui keegi ütleb, et x on selle võrrandi muutuja, siis teame, et otsime just x-ile sobivaid väärtuseid ning teised tähed tähistavad ainult teatavaid kordajaid. Konkreetsel juhul võime tundmatu x leidmiseks võrrandi mõlemalt poolt lahutada arvu a ning leida, etx = b – a. See on üldkujus võrrandi lahend.

Milleks meile üldse üldkujus võrrandid? Nad teevad elu lihtsamaks, aidates lahendada korraga palju erinevaid võrrandeid.

Näiteks ülaltoodud üldkujus võrrandi abil lahendasime ühekorraga ära kõik kolm järgnevat võrrandit:

Esimesel juhul peame valima lihtsalt a = 2, b = 4 ja saame lahendiks x = 2. Teisel juhul valime a = 3, b = 6 ja vastus on x = 3 ning kolmandal juhul annab a = 9,b = 14 valik lahendi x = 5.

Loomulikult võiksime tundmatu võrrandis tähistada ka tähega a ning kordajaid hoopis tähtedega x ja y. Sel juhul peaksime aga iga kord võrrandi juures hoolikalt täpsustama, mis on tundmatuks. Kokkulepe, et just xpeaks enamasti olema tundmatu rollis, teeb matemaatika lugemise lihtsalt kergemaks ja kiiremaks. Kui meeldiv on näiteks lugeda järgmises kujus ruutvõrrandit ja tema lahendivalemit?

Kuna selline tähistus hirmutab ja tekitab parasjagu segadust, üritame raamatus kõike tähistada võimalikult levinud sümbolitega.

Muutuja ja funktsioonid

Muutujad tulevad esile ka funktsioonidest rääkides.

Funktsiooni peatükis kirjeldame, et funktsioonist võib mõelda kui teatud masinast, mis võtab muutuja ning teeb temaga mingi operatsiooni või teisenduse. Vahel kutsutakse teda ka funktsiooni argumendiks [lk 64].

Näiteks öeldakse, et ruutfunktsioon on ühe muutujaga funktsioon ehk masin, mis võtab muutuja ja korrutab teda iseendaga. Kui anname muutujale väärtuse 3, saame vastuseks 9, andes muutujale väärtuse 5, saame vastuseks 25.

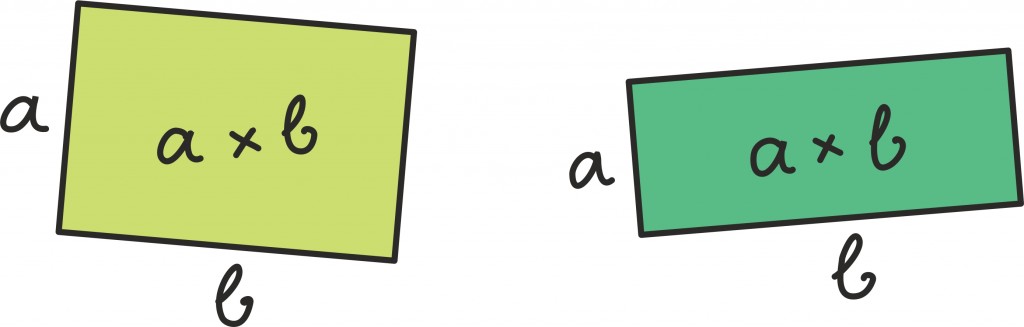
Ristküliku pindala valem

on aga juba kahe muutujaga funktsioon: võime ju muuta mõlemat ristküliku külge ja pindala aina aga muutub.

Muutuja ja summad

Muutuja võib esile tulla ka pikkades keerulistes summades või integraali nimelises monstrumis [lk 340], aidates matemaatikul end kompaktsemalt ja täpsemalt väljendada.

Kui matemaatik tahab kokku liita arvud ühest kümneni, väljendab ta ennast aga nii:

mida loeme järgnevalt: summeerime üle kõikide arvude i, alates arvust  1  kuni arvuni 10 välja:

Seda hirmsat kõverikku ei maksa sugugi karta. Tegemist on suure kreeka sigma ehk meie S-iga, mis näeb välja nagu ohutu liblikas. Meie jaoks on ta aga lihtsalt kokkuleppeline tähistus summeerimise jaoks.

Näiteks

või

Neile, kes on veidi programmeerinud, on see muidugi vägagi   selge – ka arvutitele meeldivad muutujad. Selle asemel, et kirjutada välja summa 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10, ütlete arvutile, et liida kokku kõik arvud i, mis on vahemikus 1, …, 10, ning kasuta liitmisel abimuutujat n, mille algväärtus on 0. Näiteks kirjutaks informaatik programmeerimiskeeles Python nii:

n = 0
for i in range(0,11) :
n = n + i
print(n)

Muutujateks oleks siin jupis nii „i” kui „n”. Esimesel real antakse muutujale väärtuseks 0. Järgmine rida ütleb, et muutujat tuleb muuta 1-st 10-ni (arve 0 ja 11 ei arvestata). Kolmas rida ütleb, et muutujale n tuleb iga kord juurde liita i väärtus. Nii ongi n-i väärtus algul 0, siis liidetakse n-ile juurde 1 ning n-i väärtuseks saabki 1. Järgmine kord on i väärtus 2 ja see liidetakse n-ile juurde ning uueks väärtuseks on 1 + 2 = 3. Lõpuks onn-i väärtus 55 ning see kuvatakse ekraanil.

Võrdus ja võrdsus