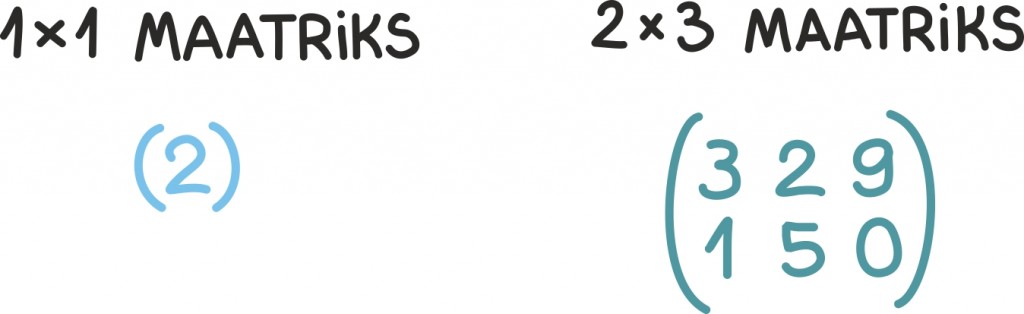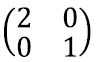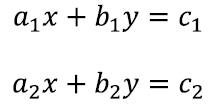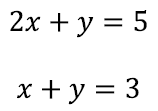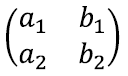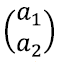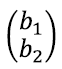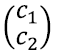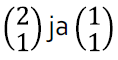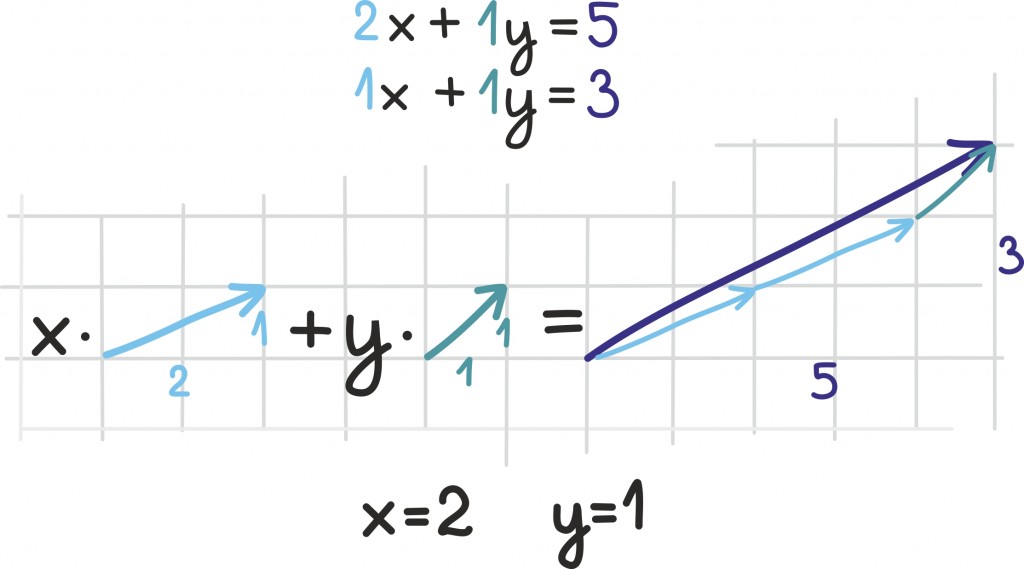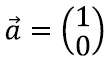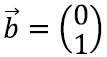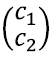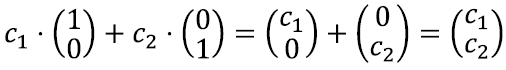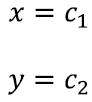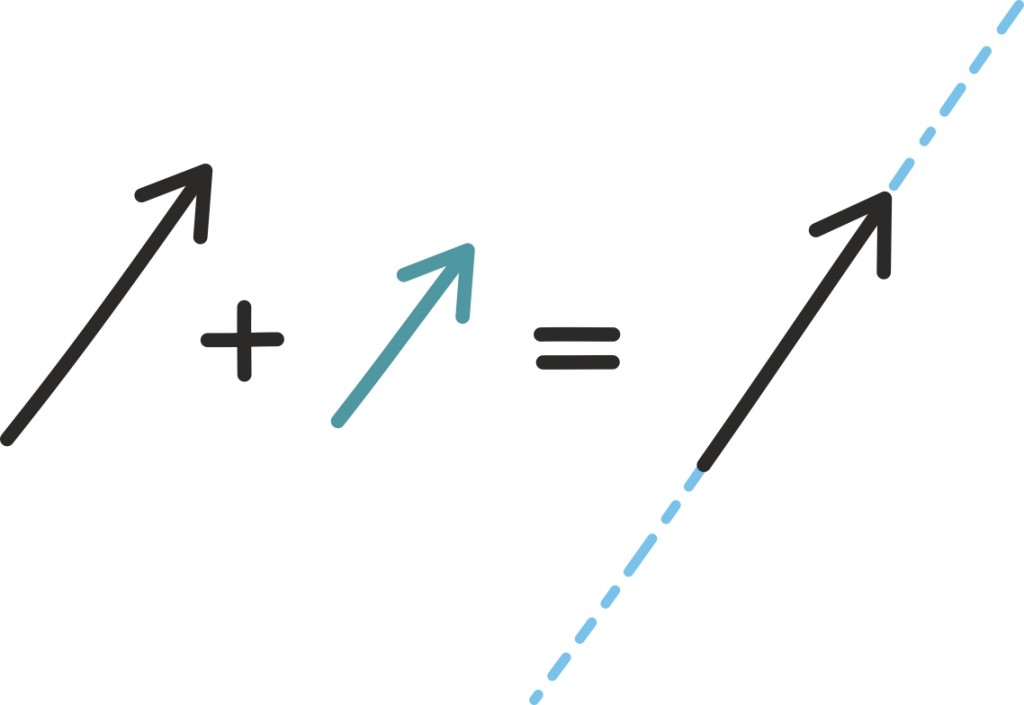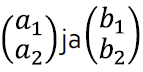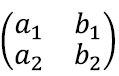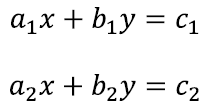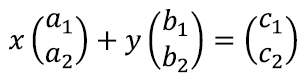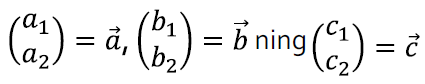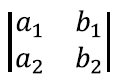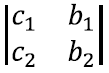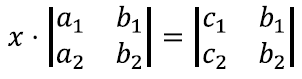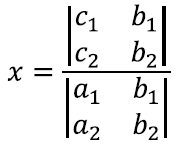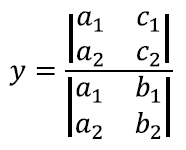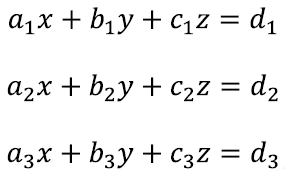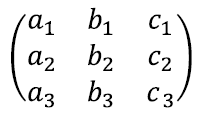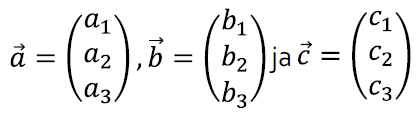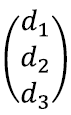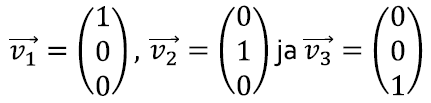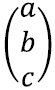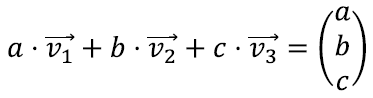Maatriks*

Nägime, et kui ühe arvu asemel seada ritta mitu arvu, saame vektori. Aga miks peaks meil ainult üks rida arve olema? Meil võiks ju olla terve arvutabel!Tõepoolest, ka arvutabelid osutuvad matemaatiliselt väga põnevaks ning neid nimetatakse maatriksiteks.

Maatriks ja võrgustikud

Maatriksite abil annab väga mõnusalt esitada toredaid andmeid ja seoseid. Näiteks võib tabelis kirjeldada neljase seltskonna sõprusvõrgustikku järgmiselt.

Nummerdame olendid arvudega 1; 2; 3; 4.
Seame lahtritesse (i; j) arvu 1, kui isikule i meeldib j, ning 0, kui ei meeldi.

Nagu näeme, on see, et isendile 1 ei meeldi ükski teine kolmest isendist, lihtsalt väljaloetav nii maatriksist kui jooniselt.

Esitus maatriksina võimaldab uurida ka palju suuremaid ja keerulisemaid võrgustikke kui meie raamatu tegelaste sõpruskond. Näiteks võime maatrikskujul esitada närvirakkude võrgustikke või rakus toimuvate protsesside vaheliste seoste võrgustikke. Närvirakkude võrgustikud võivad olla kuni 10 miljardi neuroniga ja nii on neid päris raske geomeetriliselt ette kujutada või kirja panna, maatrikskirjeldus aitab neid siiski arvutite abil uurida.

Sulle võivad huvi pakkuda need õppematerjalid:

Maatriks ja vektorid

Meid huvitab aga siin raamatus pisut teistmoodi, geomeetriline mõtteviis maatriksitest.

Idee on vaadata iga arvutabeli veergu kui ühte vektorit. Nii annab näiteks 3 × 3 maatriks kolm kolmemõõtmelist vektorit, 3 × 2 kaks kolmemõõtmelist vektorit ja 2 × 2 maatriks kaks kahemõõtmelist vektorit.

Märkame, et nüüd ja edaspidi selles peatükis ei kirjuta me vektoreid enam arve ritta seades, vaid neid tulpa ladudes. See vahetus teeb edasise kirjutamise lihtsalt mugavamaks.

Selline vaatevinkel aitab meil varsti siduda maatriksid ka lineaarvõrrandite süsteemiga.

Determinant ja lineaarvõrrandisüsteem

Kuigi väga põnevaks osutuvad nii 4 × 10, 10 × 10, 30 × 2 kui muu suurusega maatriksid, keskendume edasises 2 × 2 ning 3 × 3 maatriksitele.

Esiteks tutvustame ühte ruutmaatriksite (ruutmaatriksis on sama palju tulpasid ja veerge) karakteristikut, mida kutsutakse determinandiks. Seejärel üritame selgitada, kuidas determinandid on seotud lineaarvõrrandisüsteemide lahenditega ning kust ikkagi pärinevad kooliõpikute mõned müstilised võrrandisüsteemide lahendamisviisid.

Käesolev peatükk ulatub kindlasti kooliprogrammist välja, aga ühtlasi aitab ehk paremini mõista teisi teemasid. Võibolla on kasulik enne lugemist lähemalt tutvuda võrrandite lahendamisega osas 4 [lk 176].

Determinant

Determinandiga tutvumist võime alustada ühest üsna ehituslikust küsimusest.

Mida saame konstrueerida kahe kahemõõtmelise vektoriga

ning mida kolme kolmemõõtmelise vektoriga

Kui kaks kahemõõtmelist vektorit pole juhuslikult samasihilised ehk kui neid ei saa asetada piki sama sirget, võime nende abil moodustada rööpküliku.

Sarnaselt saame, juhul kui kolm kolmemõõtmelist vektorit ei asu ühel tasandil, ehitada nende abil kena rööptahuka.

Mõlemal juhul on neil geomeetrilistel kujunditel üks kena parameeter – nende maht. Ruutmaatriksi determinant kirjeldabki seda mahtu.

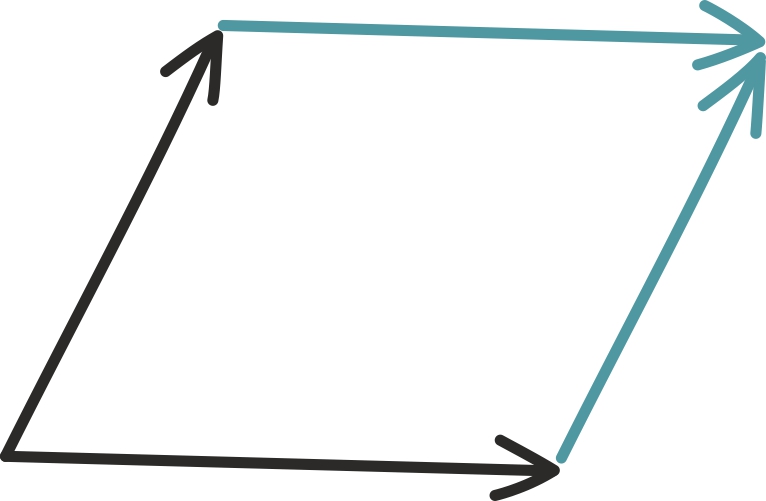
2 × 2 maatriksi puhul on tema determinandi absoluutväärtus võrdne kahe tulpvektori poolt moodustatud rööpküliku pindalaga.

Näiteks maatriksi

determinandi absoluutväärtus on võrdne kahega, kuna maatriksi tulbad kirjeldavad ristkülikut küljepikkustega 2 ja 1. Tuletame meelde, et rööpküliku pindala andis meile ka vektorkorrutise pikkuse. Tõepoolest, 2 × 2 maatriksi determinant annabki tema tulpvektorite vektorkorrutise pikkuse.

3 × 3 maatriksi puhul on determinandi absoluutväärtus võrdne kolme tulpvektori poolt moodustatud rööptahuka ruumalaga.

Determinantide abil võib otsustada, millal lineaarvõrrandisüsteemidel lahendid leiduvad ning kuidas neid lahendeid ka leida. Järjepanu need küsimused nüüd ette võtamegi.

Millal leidub kahe muutujaga lineaarvõrrandisüsteemil lahend?

Tuletame meelde, et kahe muutujaga lineaarvõrrandisüsteemi võib üldkujus kirja panna järgnevalt:

Kõigil kümnel tähistusel on siin oma roll ja see pole sugugi segaduse tekitamine. Arve a₁, a₂, b₁, b₂, c₁ jac₂ vaatleme kui juba teadaolevaid arve. Tähistame neid tähtedega, lihtsalt et käsitleda paljusid võrrandeid korraga [lk 48]. Seega palub käesolev võrrandisüsteem lihtsalt leida väärtused kahele tundmatule x ja y, nii et võrdusmärgid kehtiksid. Näiteks võiksime anda teadaolevatele arvudele kindlad väärtused ning saada konkreetsema näite:

Neid kahte lineaarvõrrandit võib ka vaadata eraldi ning kirjeldada näiteks sirgega nagu võrrandite peatükis [lk 184].

Võrrandisüsteemi lahendamiseks tuleb kaks võrrandit omavahel kuidagi siduda. Üks võimalus seda teha on seada mõlemad võrrandeid kirjeldavad sirged ühele koordinaattasandile [lk 184]. Veel kavalam on aga kasutada maatriksit:

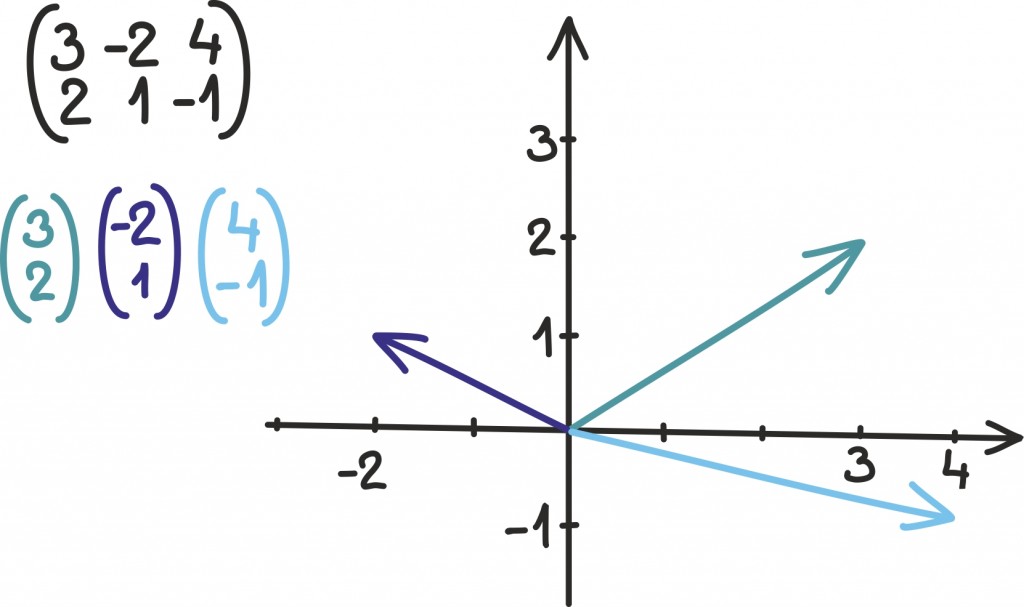
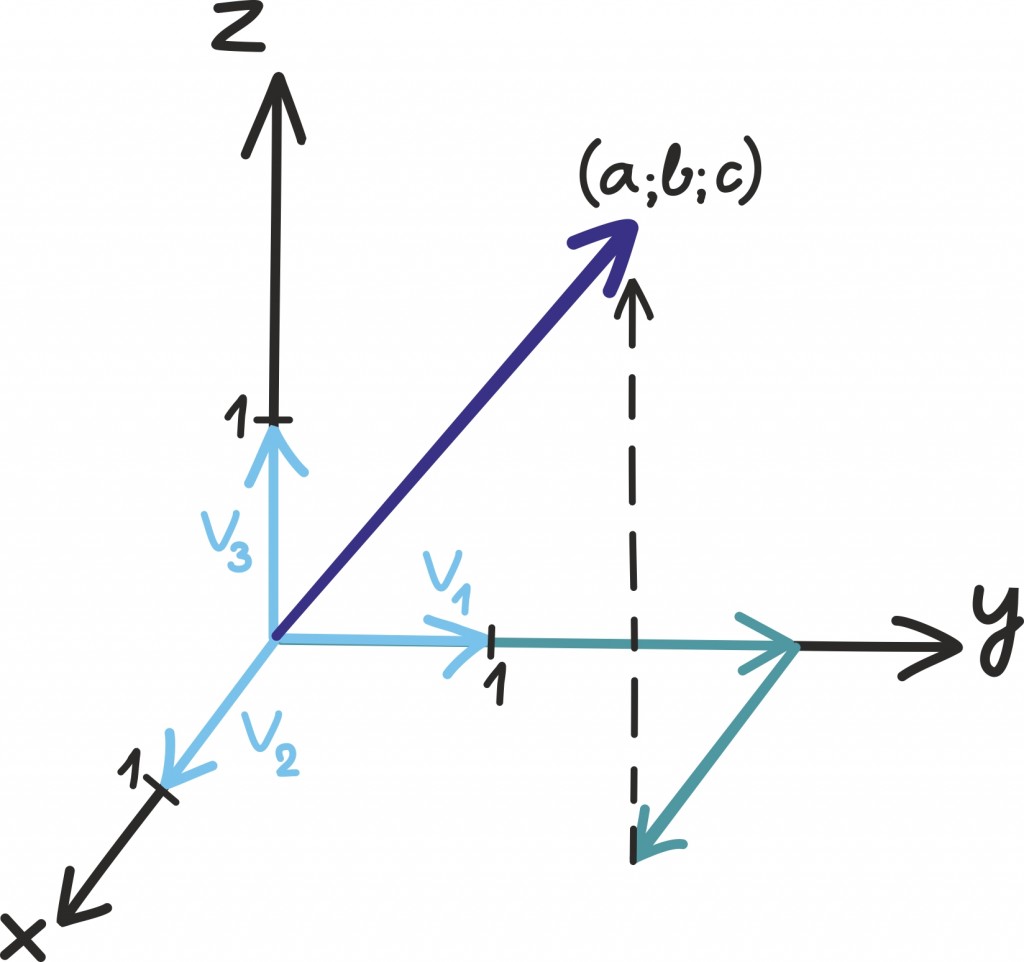
Nagu enne kirjeldasime, võime mõelda tulpadest

kui kahemõõtmelistest vektoritest, ja kuna tulpasid on tüütu pidevalt välja kirjutada, tähistame neid vastavalt

Lineaarvõrrandisüsteemi lahendamisest võime nüüd mõelda järgnevalt: eesmärk on leida reaalarvud x jay, nii et saame vektori

kirjutada vektorite

summana:

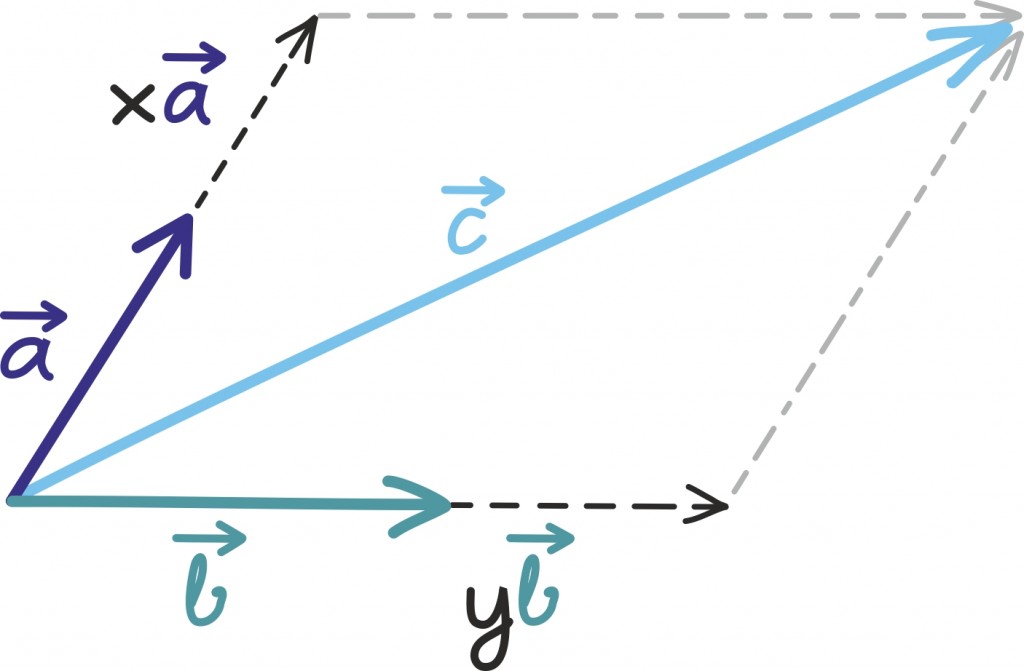
Esialgu on lihtsam seda ette kujutada joonise ja konkreetse näite abil: joonistame vektorid

ning üritame neid kokku liita, nii et saaksime vektori

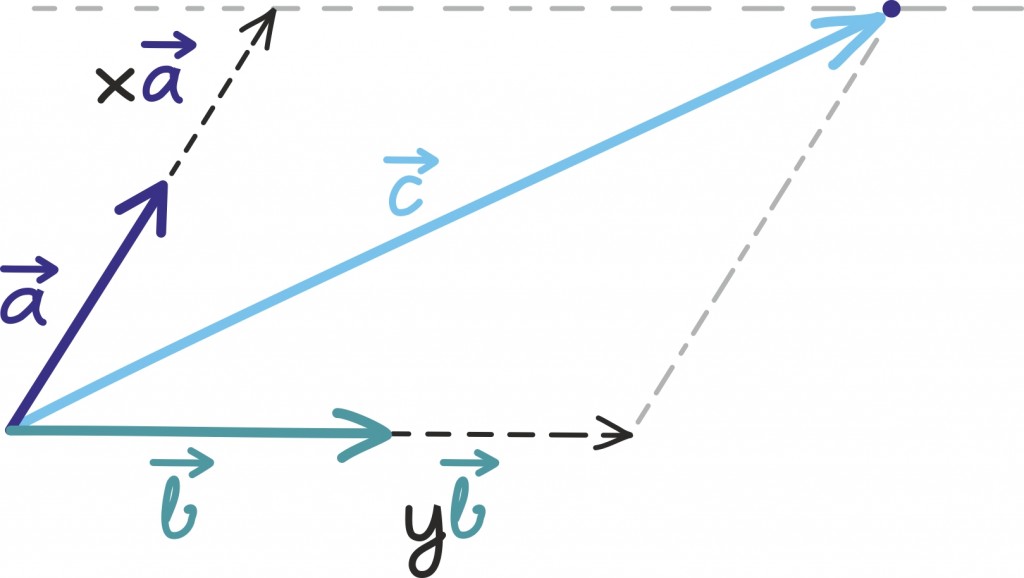
Milal on see võimalik? Kui meile on antud kaks vektorit, siis millal saame neid pikendades/lühendades ja liites esitada mingi kolmanda vektori?

Kui kaks antud vektorit oleksid

x ning y-telje ühikuid kirjeldavad vektorid, siis saaksime muidugi selle protsessi käigus kätte iga teise vektori. Vektor

on võrdne lihtsalt

See on ilmne ka võrrandisüsteemist endast. Sel juhul oleks süsteem väga lihtsas kujus

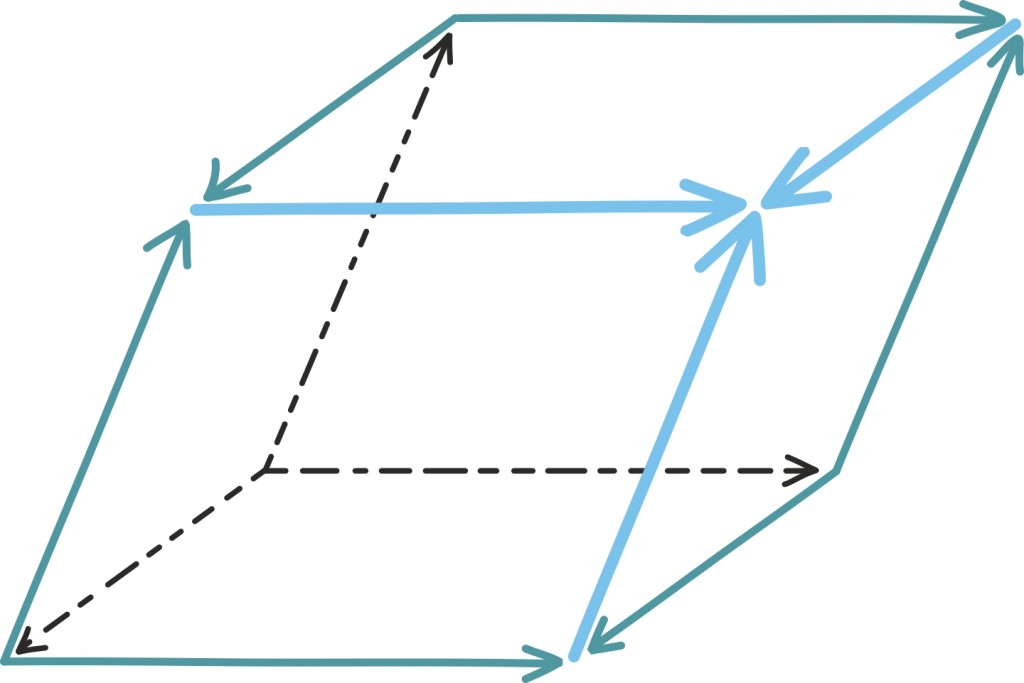
Põnev on – ja selles võib hea usu korral usina joonistamise abil veenduda –, et olukord on sarnane peaaegu iga algvektorite valiku korral! Peaaegu alati saame iga kolmanda vektori esitada antud kahe vektori summana ja seda ühel ja ainsal viisil.

Ainult juhul kui vektorite poolt moodustatud rööpküliku pindala on 0 ehk ainult siis, kui vektorid on samasihilised, pole see võimalik. Sel juhul saab nende summana esitada ainult teisi samasihilisi vektoreid.

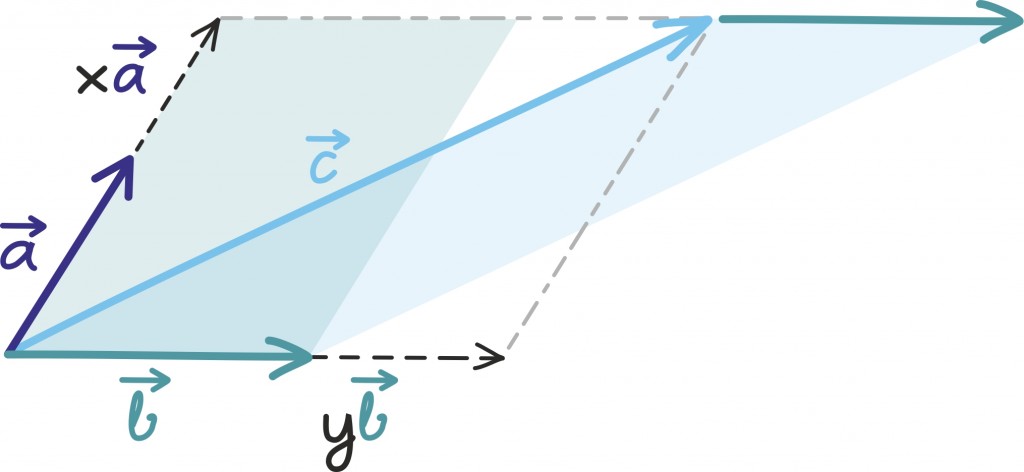
Nüüd aga tuletame meelde, et vektorite

poolt moodustatud rööpküliku pindala oli võrdne maatriksi

determinandiga.

Sellest järeldubki õpikutest leitav tingimus:

kui determinant pole võrdne nulliga ja seega vektorid

pole samasihilised, leidub võrrandisüsteemile alati täpselt üks lahend,
kui aga determinant on võrdne nulliga ja seega vektorid

on samasihilised, leidub null või lõpmatult palju lahendeid:
- kui vektor
  
  on vektoritega
  
  samasihiline, leidub lõpmatult palju lahendeid ja
- muul juhul ei leidu ühtegi lahendit.

Järgnevalt lähme sammu edasi ja näitame, kuidas determinantide abil ka kahe muutujaga lineaarvõrrandi süsteemi täpsed lahendid üles leida.

Kahe muutujaga lineaarvõrrandisüsteemi lahendamine determinandiga

Nagu nägime, võime lineaarvõrrandisüsteemi

vektorite abil kirja panna järgnevalt:

Mugavuse ja tindi kokkuhoiu eesmärgil tähistame tulpvektorid jälle järgmiselt:

Seega saame võrrandi:

Teisisõnu, tahame vektoreid

parasjagu lühendada ja pikendada, just niipalju, et nende kokkuliitmisel saaksime kolmanda vektori

Oletame, et

ei ole samasihilised ning nendest võib moodustada ilusasti rööpküliku. Just selle rööpküliku abil võime siis visualiseerida ka oma ülesannet:

Lühendamise ja pikendamise mahtu kannavad endas reaalarvud x ja y. Kuidas nende suurust leida?

Joonise abil märkame, et meie otsitav arv x peab vektori otspunkti viima „sama kaugele” vektorist

kui on vektori

otspunkt.

Nüüd tuletame meelde, et rööpküliku pindala võime kirjutada tema aluse ja kõrguse korrutisena [lk 366]. Nii saame omavahel võrduma panna kaks võrdse pindalaga rööpkülikut:

esiteks rööpkülik, mis tekib vektorite

vahele,
teiseks rööpkülik, mis tekib vektori

vahele.

Tõepoolest, mõlema alus on ning nende kõrgused on samad.

Puhtalt sellest tähelepanekust võimegi tuletada muutujale x sobiva väärtuse. Nimelt rööpkülik, mis on tekkinud vektoritest

on x korda „kõrgem” kui rööpkülik, mis tekib vektoritest

Samas teame, et vektorite

vahele tekkiva rööpküliku pindala kirjeldab just determinant

Seega on intuitiivselt üsna selge, et vektoritele

ehitatud rööpküliku pindala leidmiseks peame determinandi

lihtsalt arvuga x läbi korrutama.

Samas on vektoritele

ehitatud rööpküliku pindala antud determinandiga

Seega saamegi võrrandi kordaja x suhtes:

Siit saame juba kergesti leida x-i enda väärtuse:

Kui sooviksime leida y-i väärtust, siis peaksime lihtsalt sama protseduuri läbi tegema, kasutades vektoreid vektoritest

Tulemuseks on:

Sarnane meetod toimib ka kolmes, neljas, kaheksas mõõtmes, kuigi selle geomeetriline ettekujutamine läheb muidugi järjest keerulisemaks. Teisisõnu saab determinantide abil lahendada ükskõik kui paljude muutujatega lineaarvõrrandisüsteeme. Saadud valemid on eriti väärtuslikud arvutitega töötamisel – nad annavad väga kiire ja vähemalt arvutite jaoks lihtsa viisi ka väga suurte lineaarvõrrandisüsteemide lahendamiseks.

Millal leidub kolme muutujaga lineaarvõrrandisüsteemil lahend?

Et kindlaks teha, kas kõik sai kenasti selgeks, arutame lühidalt läbi ka kolme muutujaga juhu. Kõik on tegelikult analoogne. Kui vaatame võrrandisüsteemi

võime moodustada maatriksi

ja mõelda vektoritest

kui kolmest kolmemõõtmelisest vektorist.

Seegi kord tahame kirjutada vektori

vektorite

lineaarse summana

Jällegi on küsimus, millal saame kolme antud vektori abil ühte antud vektorit nõnda kirjeldada, ja on ilmne, et vektorite

korral on see alati võimalik.

Näiteks vektori

saaksime, kui korrutaksime vektorid

vastavalt reaalarvudega a, b ja c ning liidaksime kokku:

Sellest on võibolla lihtsam mõelda hoopiski graafiliselt:

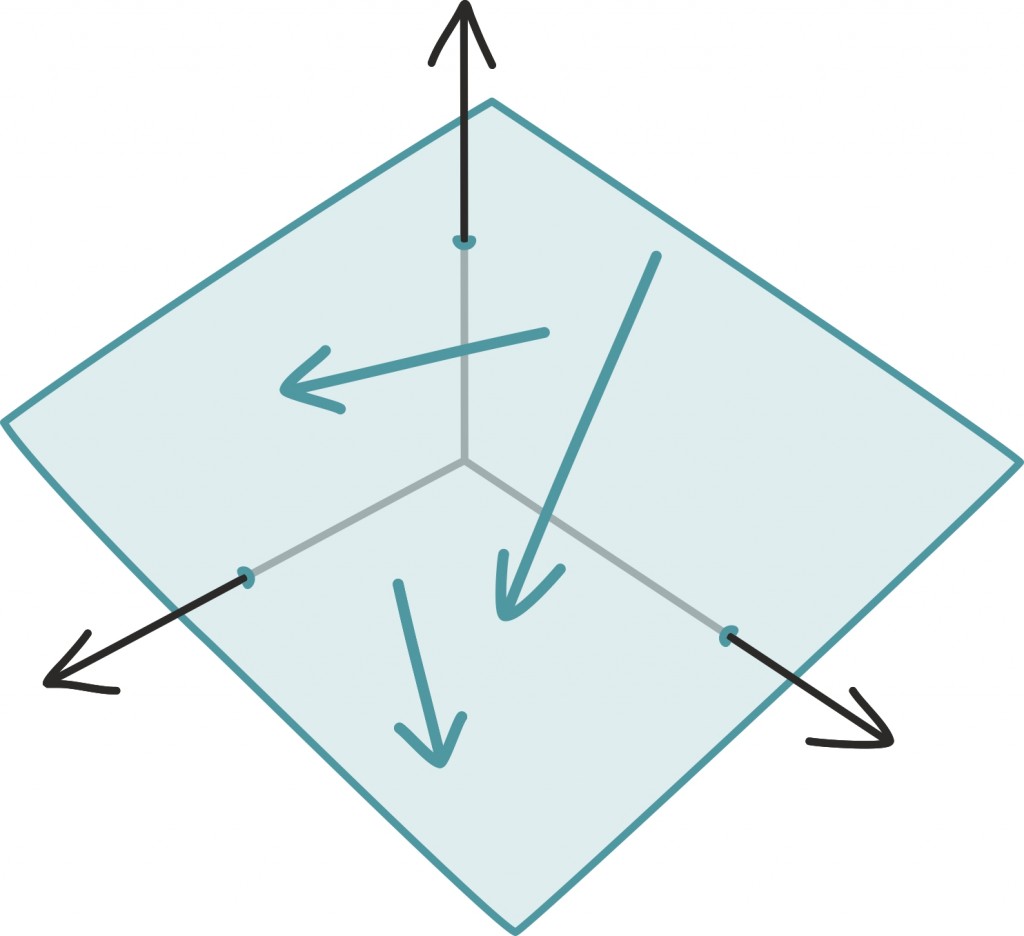
Selgub, et ka ainus takistus on väga sarnane kahemõõtmelisele juhule – iga vektori

saame vektorite

lineaarse summana ühel moel kirjutada just siis, kui vektorid

ei asu kõik ühel tasandil, ehk teisisõnu kui nende poolt moodustatud rööptahuka ruumala pole null. Kui vektorid asuvad aga ühel tasandil, saab nende summana esitada ainult sel samal tasandil esitatavaid vektoreid.