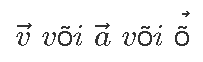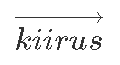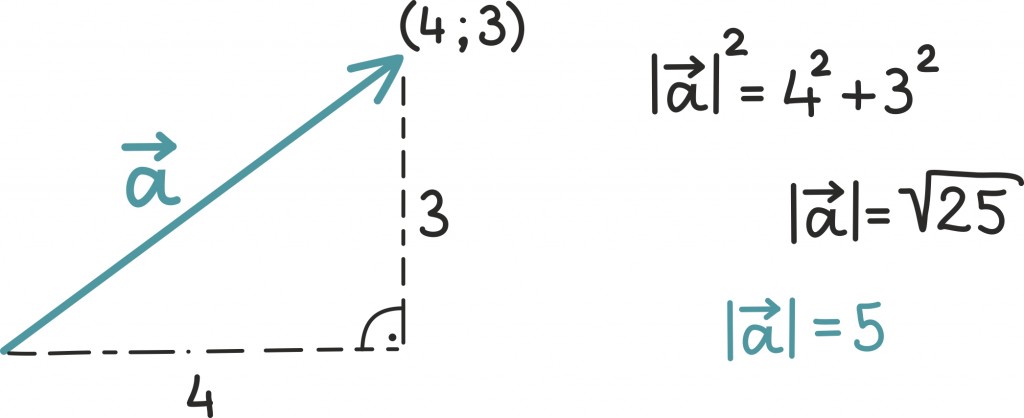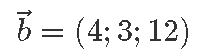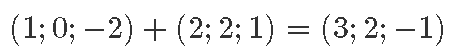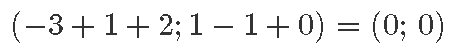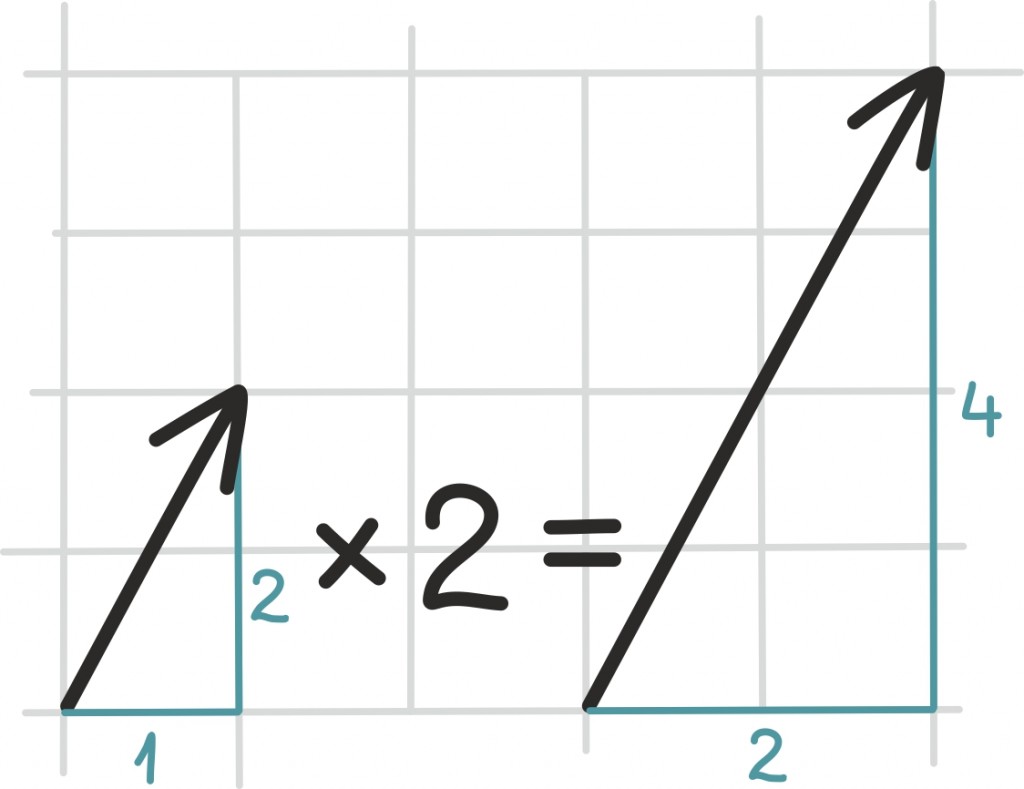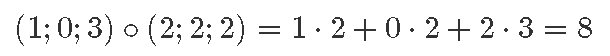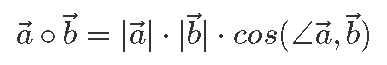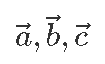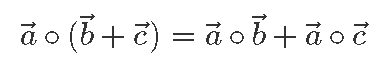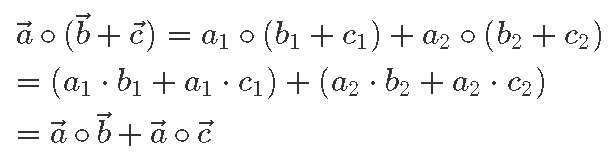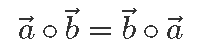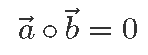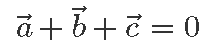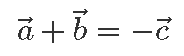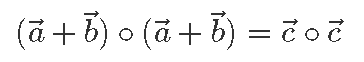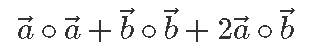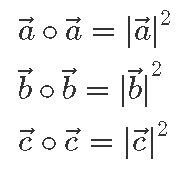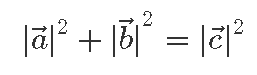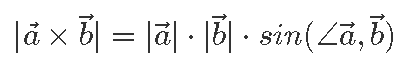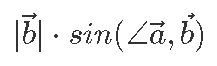Vektor
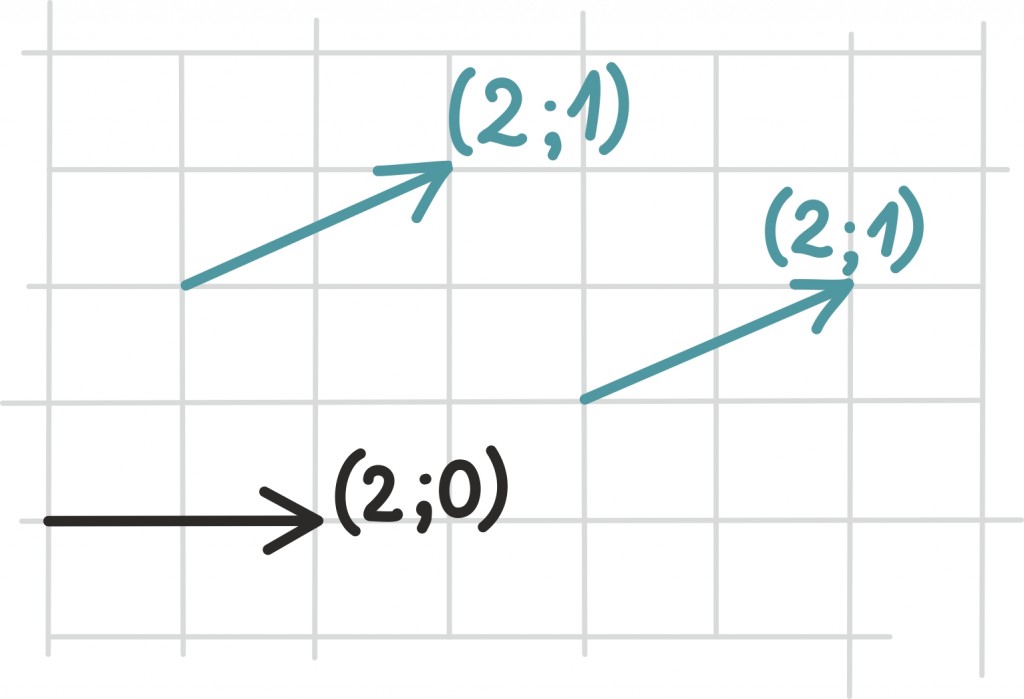
Kui eelmise peatüki lõpetasime väikese mõistatusega, siis seekord alustame väikese mõistatusega: mis on pildil?
Tahtsite vastata nooled? Ei, matemaatiku, füüsiku ning hoolsa koolijütsi jaoks on need hoopis vektorid!
Vektoritest võibki lihtsalt mõelda kui nooltest. Nagu iga noolt, iseloomustab vektoreidki teatav suund ja teatav pikkus. Vektorid osutuvad oluliseks, kuna nende abil võib kirjeldada objekte, mille puhul on olulised nii nende suund kui tugevus.
Näiteks professionaalsed tuulelohetajad (või purjetajad) on kindlasti uurinud kohaliku piirkonna tuulte kaarti – sealsed paljud nooled, mis kirjeldavad tuulte suunda ja tugevust, on tuulevektorid.
Samuti on füüsikutel kombeks rääkida jõuvektoritest: kui ikkagi kellegagi kätt surute, tuleb jõudu avaldada nii teatud tugevusega kui ka õiges suunas.
Kuidas vektorit matemaatiliselt kirja panna?
Kahemõõtmeline vektor ei ole midagi muud kui lihtsalt reaalarvude paar – näiteks (1; 3). Kolmemõõtmeline vektor on tavaline reaalarvude kolmik – näiteks (3; 0; 2).
Kena näide kümnemõõtmelisest vektorist on igal juhul (0; 1; 2; 3; 4; 5; 6; 7; 8; 9) ja mis on kahe tuhande üheteistkümne mõõtmeline vektor, pole vist ka keeruline välja nuputada… kuigi võib olla keerulisem kirja panna.
Et seost nooltega meelde tuletada, tähistatakse vektoreid ka tavaliselt tähe ja noolekesega, nagu näiteks
Muidugi ei keela keegi näiteks liikumisvektorile nimeks panna
ainult kirjavaeva oleks nii rohkem.
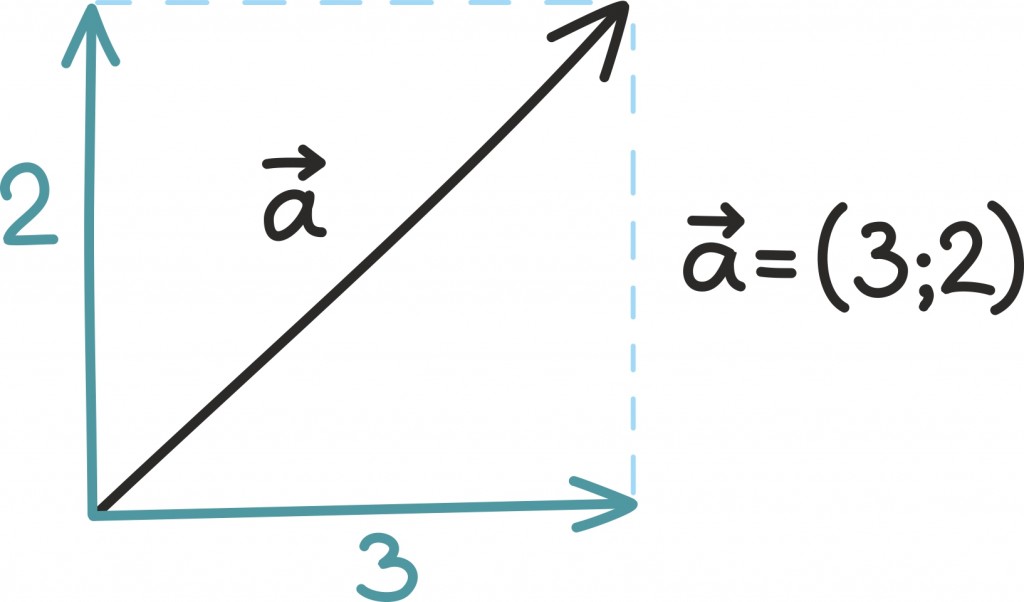
Arvulise kirjapaneku ja visuaalse mõtte vahelist seost illustreerib järgmine joonis. Kahemõõtmelist vektorit kirjeldavad kaks arvu (mida kutsutakse koordinaatideks) näitavad, kui kaugele ulatub nool kahes ristuvas suunas. Kolmemõõtmelise vektori korral oleks meil juba vaja kolme ristuvat suunda, neljamõõtmelise joonistamine läheks juba raskeks…
Sulle võivad huvi pakkuda need õppematerjalid:
Hariliku murru kordamine
Ratsionaalavaldised
Funktsioonide graafikute lõikepunktide leidmine
xy-koordinaatsüsteem
Kirjalik liitmine
Algebralised murrud
Funktsioonid ja nende graafikud
Tasandilised kujundid
Kell ja kellaaeg
Ruutvõrrandi abil lahenduvad tekstülesanded
Liitmine ja lahutamine 10 piires
Funktsioonide graafikud
Ruumilised kujundid
Peastarvutamine I kooliastmele
8. klassi matemaatika teooriavideod
Liitmine ja lahutamine 20 piires
II kooliastme matemaatika reeglite kordamine
Liitmine 10 piires
Kirjalik lahutamine
Ruutvõrrand
.
Vektoritega mängimine
Vektorile on väga lihtne intuitiivne selgitus – nooleke pikkuse ja suunaga. Ometi on vektoril kui matemaatilisel objektil palju erinevaid omadusi, teda võib mitmel moel teisendada ning temaga teha erinevaid tehteidki.
Sellest lähtuvalt on kogu see alapeatükk täis uusi mõisteid ja trikikesi, millest ühe korraga läbinärimine võib olla üsna väsitav. Nii soovitamegi vaadata kõiki järgnevaid kirjutusi ühe- või kahekaupa ja iga omaduse, teisenduse ja tehte juures võtta kõrvale mõni konkreetne näide, nägemaks, et midagi keerulist kogu peatükis siiski pole.
Võrdsed vektorid
Kui oleme defineerinud mõne uue matemaatilise objekti, siis on esimene loomulik küsimus: millal on kaks sellist objekti võrdsed? Ehk millal on kaks vektorit võrdsed?
Õnneks on vektorite puhul vastus üsna ilmne ja lihtne. Kui mõelda vektorist kui mitmest ritta seatud arvust, on üsna kärmelt selge, mida peaksid tähendama võrdsed vektorid: kõik vektori koordinaadid peavad olema võrdsed.
Vektori pikkus
Vektori  pikkust |
pikkust | |arvutame täpselt nagu punkti kaugust nullpunktist. Seega kahemõõtmelise vektori pikkuse võime välja arvutada nii nagu ikka täisnurkse kolmnurga hüpotenuusi.
|arvutame täpselt nagu punkti kaugust nullpunktist. Seega kahemõõtmelise vektori pikkuse võime välja arvutada nii nagu ikka täisnurkse kolmnurga hüpotenuusi.
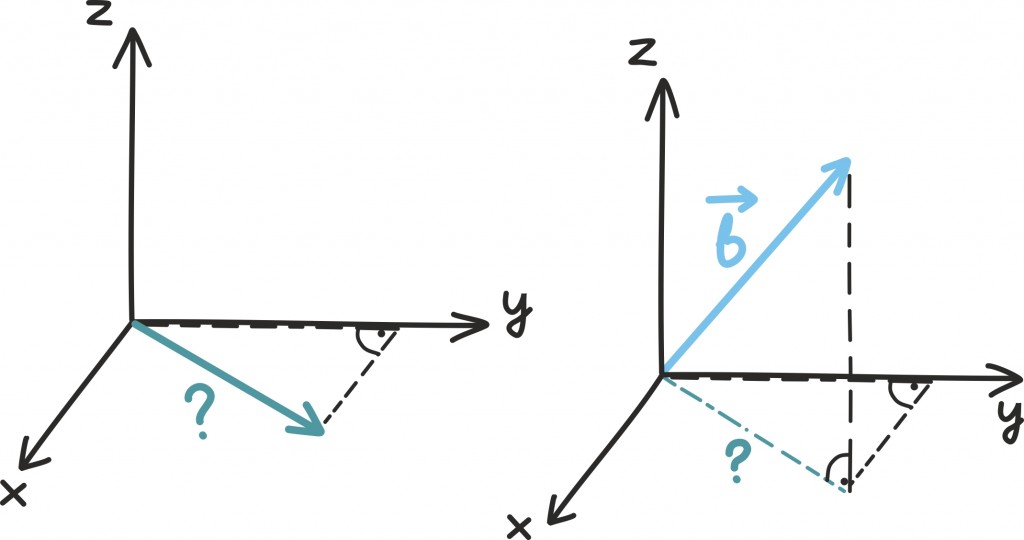
Juhul kui vektor on kolmemõõtmeline, peame seda arutluskäiku rakendama lihtsalt kaks korda. Siin on näide vektoriga
Vektorite liitmine
Vektorite liitmisest saame mõelda mitmel viisil. Vektoreid on vaja liita näiteks siis, kui tahame kokku liita mitu erinevat ühele objektile mõjuvat jõudu.
Esmalt võime liitmisest mõelda arvulise esituse abil. Sel juhul teeme seda koordinaatide kaupa: näiteks
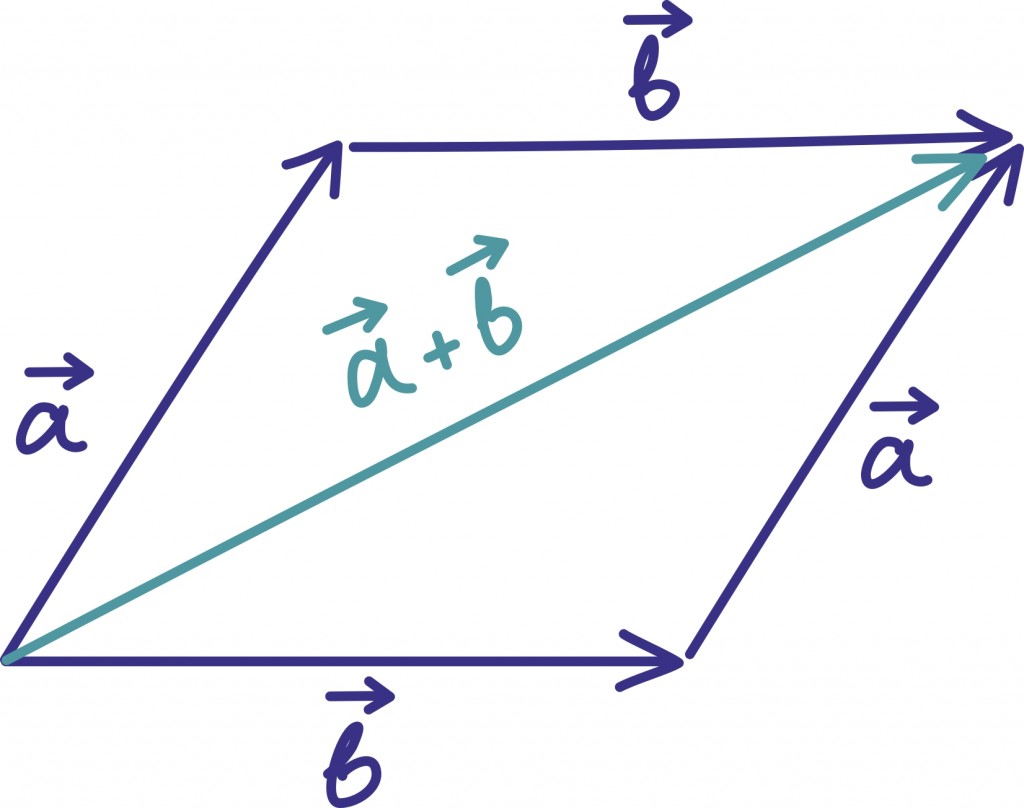
Samas võime vektorite liitmisest mõelda ka geomeetriliselt. Summavektori leidmiseks peame lihtsalt liidetavad vektorid teineteise järele seadma.
Summavektor viib niisiis esimese vektori alguspunktist teise lõpp-punkti. Toodud jooniselt on hästi näha, miks geomeetrilist liitmist kutsutakse ka „rööpküliku reegliks”.
Toodud geomeetriline mõtteviis annab hea tõlgenduse juhule, kui näiteks kolme või nelja või kuue vektori summa on null.
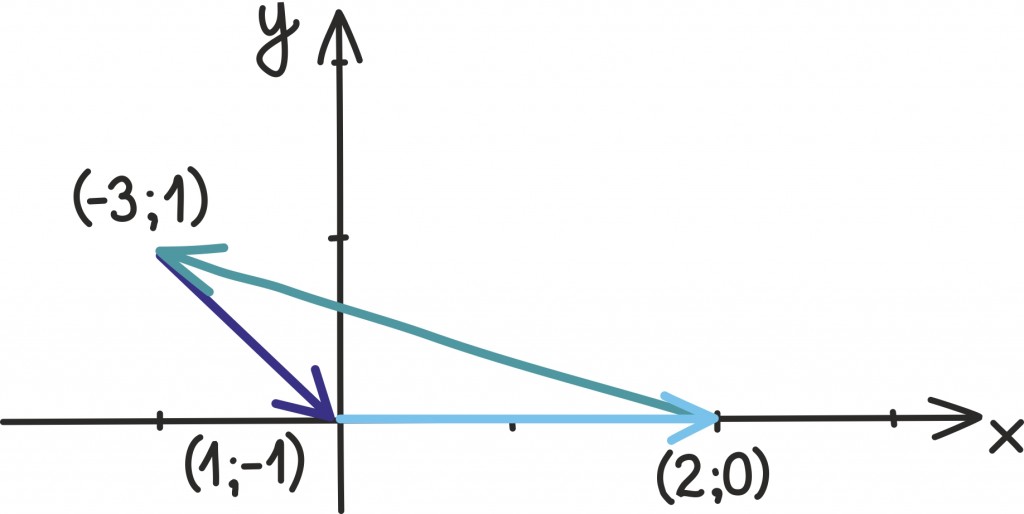
Tõepoolest, kui kolme vektori summa on null, siis peab kolmanda vektori lõpp-punkt olema esimese vektori alguspunktiks ning joonisele tekib kolmnurk. Näiteks kui meil on vektorid (–3; 1), (1; –1) ja (2; 0), siis kokku liites saame tõesti nullvektori
Samamoodi kui näiteks nelja vektori summa on null, defineerime selle abil nelinurga, ja kui kuue vektori summa on null, siis kuusnurga.
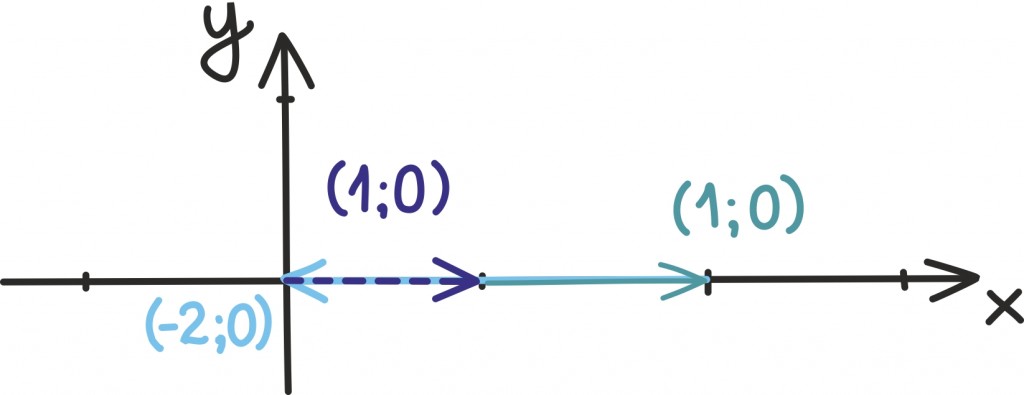
Hoolikas lugeja muidugi märkab, et oleme siin natuke luisanud. Kui võtame vektorid (1; 0), (1; 0) ja (–2; 0) siis ei teki ju siiski kolmnurka, sest kõik vektorid on samal sirgel.
Õnneks ongi see pisiasi ainus, mis saab muidu nii ilusa seose untsu ajada.
Nullvektor, vastandvektor
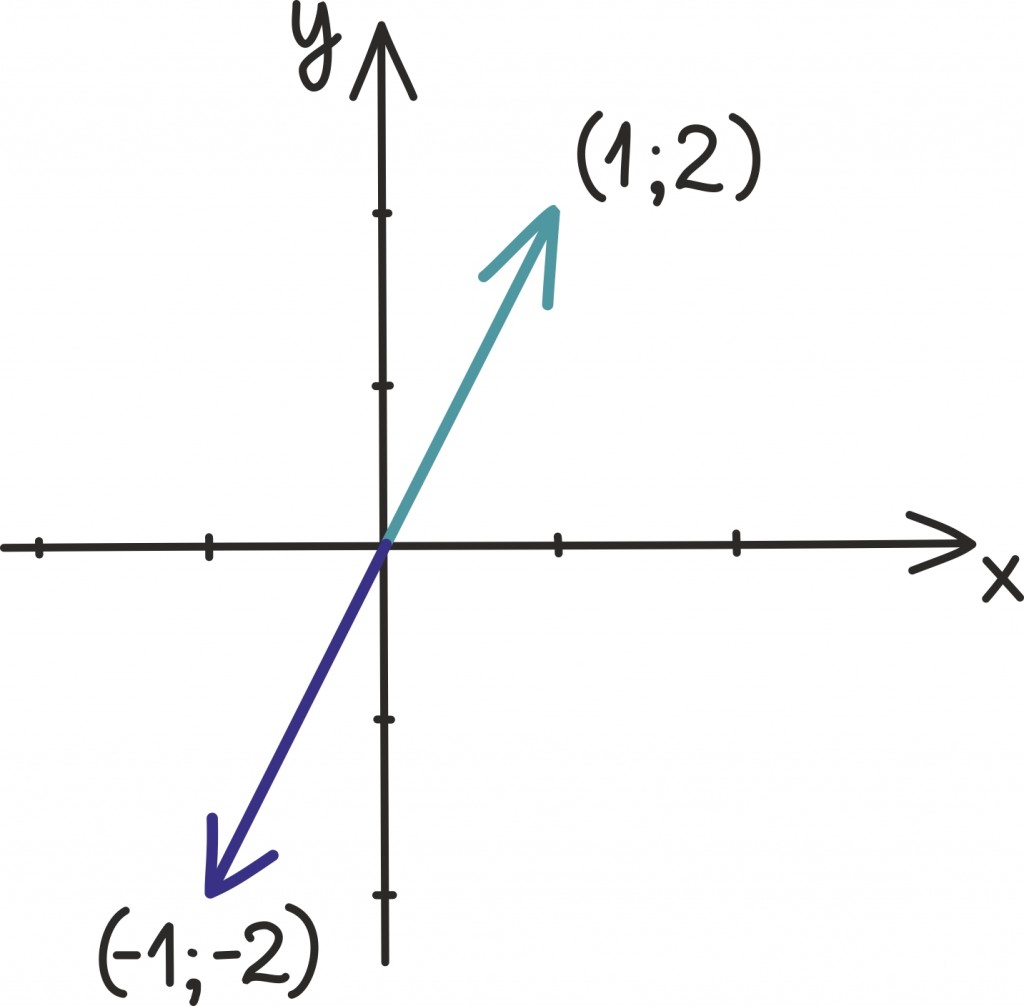
Arvude liitmisel on ühel arvul eriline roll: arv null. Mõnda arvu temaga kokku liites saame tulemuseks selle arvu enda. Analoogne objekt vektorite hulgas on nullvektor: vektor, millega liitmisel on tulemuseks vektor ise. Kolmemõõtmeline nullvektor on siis muidugi (0; 0; 0). Sarnaselt arvudega võib siis defineerida ka vastandvektori: vektori, millega liitmisel saame tulemuseks nullvektori. Näiteks vektori (1; 2) vastandvektor on (–1; –2).
Vektorid ja korrutamine
Vektoreid võime reaalarvudega korrutada. Sellest võib jällegi mõelda vektori koordinaatide abil: korrutame lihtsalt iga koordinaati reaalarvuga.
Samas on olemas ka geomeetriline mõtteviis: vektorit reaalarvuga korrutades pikendame või lühendame vektoreid. Kui reaalarv, millega vektorit korrutame, on negatiivne, siis muudame lisaks veel vektori suuna vastupidiseks.
Seega ei ole väga raske korrutada vektoreid reaalarvudega. Aga kas vektoreid saab ka omavahel korrutada?
Vastus on jällegi jah, aga selle jaoks peame natuke loobuma oma senisest arusaamast korrutamise kohta. Õigem oleks siis võib-olla öelda, et neid saab omavahel „korrutada“.
Õigupoolest saab vektoreid omavahel korrutada mitmel moel, aga kuna ükski neist ei ole päris analoogne arvude korrutamisega, on neile antud ka eraldi nimetused: 1) skalaarkorrutis ja 2) vektorkorrutis. Kahe vektori skalaarkorrutis annabtulemuseks lihtsalt reaalarvu, vektorkorrutis aga jälle ühe uue vektori.
Omaette küsimus on muidugi, miks peaksime tahtma vektoreid üldse omavahel „korrutada”. Matemaatiliselt on see soov üsna loomulik, kuna kõik hästi valitud teisendused ja tehted kannavad endas lootust luua rohkem seoseid erinevate matemaatika harude vahel ning seega võivad viia parema arusaamani kogu matemaatikast.
Õnneks leidub praktilisele lugejale siiski ka eluline vastus: nimelt nagu varsti näeme, on füüsikutel nii skalaarkorrutise kui vektorkorrutise jaoks olemas igati intuitiivne ja looduslik tõlgendus: skalaarkorrutis näitab, mil määral füüsikalised suurused töötavad ühe eesmärgi nimel. Näiteks kui üht keha liigutatakse teatavas suunas ühe jõu abil, siis skalaarkorrutis annab meile teada, kui palju tehti keha liigutamisel kasulikku tööd. Vektorkorrutis omakorda aitab kirjeldada, mil määral üks või teine jõud suudab kehasid pöörlema panna.
Lisaks selgub, et skalaar- ja vektorkorrutis osutuvad oluliseks arvutigraafikas. Nimelt võib nende abil taandada kõiksugu geomeetrilised teisendused nagu pöörded, peegeldused puhtalt koordinaatidega arvutustele, millega arvutid kenasti toime tulevad.
Lõpetuseks võib õhku jääda muidugi küsimus: kas vektoreid kuidagi omavahel „jagada” ka saab?
Seekord saame lõpuks vastata „ei“, vähemalt skalaarkorrutise ja vektorkorrutise jaoks jagamistehet ei leidu. Põhjus on üsna proosaline – kui me fikseerime ühe vektori, siis leidub terve hulk teisi vektoreid, mis temaga „korrutades” annavad täpselt sama skalaar- või vektorkorrutise. Näiteks vektoriga (1; 0; 0) annavad skalaarkorrutise null kõik vektorid kujus (0; a; b) . Need moodustavad aga kogu y–z tasandi ja me ei suuda nende hulgast jagamistehte vastust välja valida!
Skalaarkorrutis
Kui intuitiivselt kannab skalaarkorrutis samasuunalisuse mõtet, siis matemaatiliselt võib skalaarkorrutisest mõelda ja teda defineerida [lk 44] kahel viisil. Need kaks viisi on ka igati samaväärsed. Seda samaväärsust tuleks matemaatiliselt tõestada, aga siinkohal piirdume siiski ainult nende kahe viisi tutvustamisega.
Skalaarkorrutis läbi koordinaatide
Üks viis skalaarkorrutise defineerimiseks on koordinaatide põhine: kahe vektori skalaarkorrutise saame, kui esmalt korrutame kahe vektori vastavad koordinaadid ning seejärel liidame kõik saadud korrutised omavahel kokku.
Tähistades skalaarkorrutist silmapaistva punktiga, võime kirjutada näiteks:
Huvitav on märgata, et nii defineeritud korrutustehte tulemuseks on reaalarv.
Ei ole sugugi lihtne kohe aru saada, miks selline üsna lihtne definitsioon võiks samaaegselt ka huvitav või kasulik olla. Teatavat lootust annab juba teadmine, et võime teda samahästi defineerida ka hoopis teisel viisil.
Skalaarkorrutis läbi vektorite vahelise nurga
Skalaarkorrutis seob ka kavalalt vektorite vahelise nurga ja nende pikkused. Ta on võrdne vektorite pikkuse ning nendevahelise nurga koosinuse korrutisega:
Kuigi sel moel on koordinaatidega antud vektorite vahelist skalaarkorrutist raskem leida, pakub see definitsioon hea viisi, kuidas skalaarkorrutisest näidete abil pisut aimu saada.
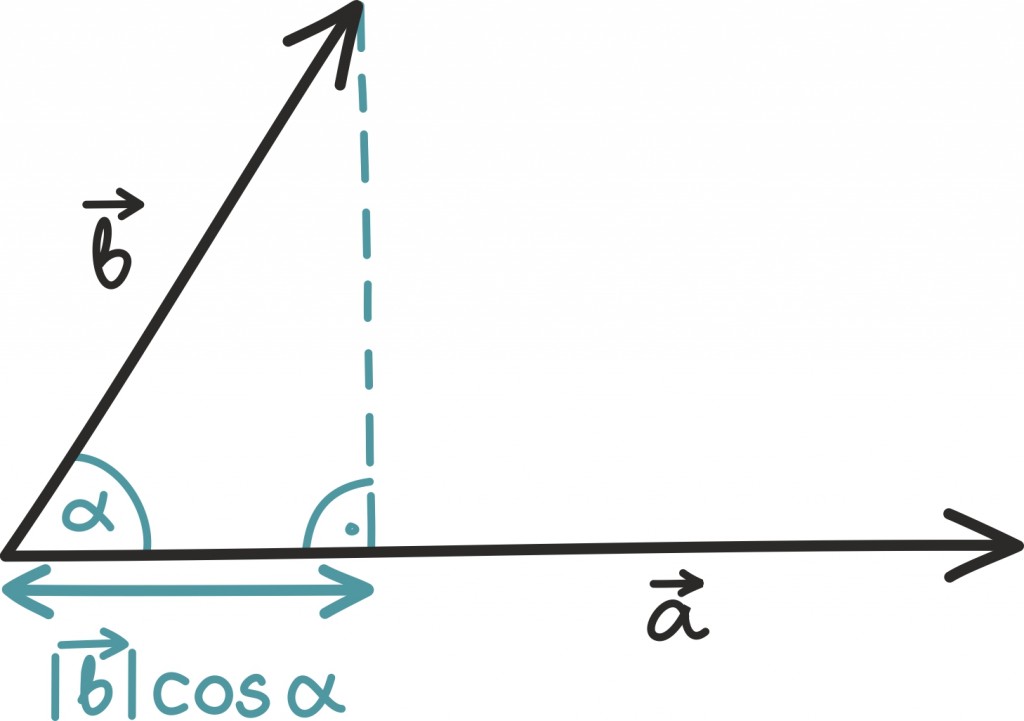
Märkame, et sellest definitsioonist lähtuvalt võime skalaarkorrutist vaadelda kui vektori  pikkuse korrutist selle osaga vektorist
pikkuse korrutist selle osaga vektorist  , mis näitab vektoriga
, mis näitab vektoriga  samas suunas.
samas suunas.
Seega
- kui üks vektoritest on nullvektor, siis skalaarkorrutis on 0, sest nullvektori pikkus on null,
- ühe vektori korrutis iseendaga annab täpselt vektori pikkuse ruudu, sest nurk vektorite vahel on 0° ja cos0° = 1 – vektorid näitavad täiesti samas suunas,
- kui kaks vektorit on omavahel risti, siis on nende skalaarkorrutis null, sest cos90° = 0.
Üldisemalt näemegi, et kahe vektori skalaarkorrutis on maksimaalne, kui vektorid on samasuunalised. Hakates vektorite vahelist nurka suurendama, skalaarkorrutis väheneb ning tema väärtus on minimaalne siis, kui vektorid on vastassuunalised.
Fakt, et skalaarkorrutist saab defineerida kahel moel, muudab tema omaduste tõestamise üsna mugavaks – vähemalt ühes kujus on iga omadust lihtne tõestada.
Samuti on erinevad kujud kasulikud erinevates probleemides: pikkuste ja nurga abil antud kuju on füüsikute lemmik, samal ajal kui arvutigraafikas on lihtsam kasutada skalaarkorrutise leidmist koordinaatide abil.
Skalaarkorrutis ja füüsika
Suur osa füüsikalistest suurustest on samuti suuruse ning suunaga – näiteks liikumine toimub ju teatud suuna ja kiirusega ning jõud mõjuvad mingis suunas ja mingi tugevusega. Skalaarkorrutis tuleb mängu füüsikaliste suuruste kombineerimisel.
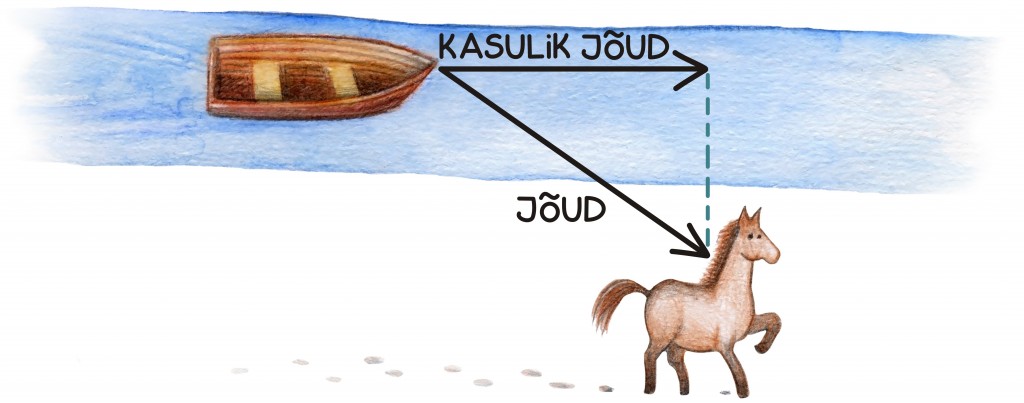
Näiteks kui vanasti kasutati hobuseid, et paati mööda jõge edasi viia, siis oli kõige targem hobust paralleelselt mööda jõeäärt talutada võimalikult kalda lähedalt.
Sellest võib mõelda skalaarkorrutise abil. Kui paat piki jõge liigub, võime tema liikumist kirjeldada kiirusvektoriga. Hobune avaldab talle tõmbamisega jõudu, mida kirjeldame jõuvektoriga. Nende vektorite omavaheline skalaarkorrutis annab nüüd ajaühikus tehtava kasuliku töö ehk võimsuse. Intuitiivselt kannab skalaarkorrutis endas teadmist, et paadi edasiliikumisele aitab kaasa ainult jõu kiirusvektori suunaline komponent. Seda võiks kutsuda kasulikuks jõuks. Tõepoolest, kui hobune tõmbaks paati risti jõega, oleksid jõuvektor ja kiirusvektor risti, skalaarkorrutis oleks null ja hobune paadi edasiliikumises rolli ei mängiks. Mida lähemal hobune jõele jalutab, seda paralleelsem on kiirusvektoriga ka jõuvektor, seda suurem skalaarkorrutis, seda suurem kasulik jõud.
Mõned skalaarkorrutise omadused ja Pythagorase teoreem*
Skalaarkorrutisel on tavalise korrutamisega mitmeid sarnaseid omadusi.
Esiteks võime koordinaatkuju abil kergesti näidata, et ka skalaarkorrutis on distributiivne: teisisõnu, iga kolme vektori
Näiteks kahemõõtmeliste vektorite  = (a1; a2) korral võime kirjutada koordinaatkuju definitsiooni abil:
= (a1; a2) korral võime kirjutada koordinaatkuju definitsiooni abil:
Samamoodi näeme emmast-kummast definitsioonist, et skalaarkorrutis on kommutatiivne, ehk vektorite järjekord skalaarkorrutise võtmisel ei loe:
Samas meenutame, et nurga abil antud definitsioonist järeldasime, et ristiolevate vektorite skalaarkorrutis on null ning vektori skalaarkorrutis tema endaga on võrdne vektori pikkuse ruuduga.
Kasutades nüüd neid kahte omadust, võime näiteks tuletada Pythagorase teoreemi.
Olgu antud täisnurkne kolmnurk, mille küljevektorid  ja
ja  on risti – ehk siis
on risti – ehk siis
Samas nägime ennist, et kolmnurga küljevektorite jaoks kehtib ka
ehk
[lk 142]
Võtame nüüd mõlema poole skalaarkorrutise iseendaga ja saame:
Kasutades peatüki alguses toodud esimest skalaarkorrutise omadust näeme, et vasema poole väärtus on
Kuid
ning
Seega tõepoolest jääb järele samasus,
mis ongi Pythagorase teoreem.
Vektorkorrutis*
Nägime, et kui keha liigub mööda sirgjoonelist trajektoori ning talle mõjub teatav jõud, võime keha liikumiskiirust mõjutava kasuliku, samasuunalise jõu leida jõu- ning kiirusvektori skalaarkorrutise abil.
Kui aga näiteks fikseerime keha kauguse teatavas keskmest (ehk pöörlemisteljest) mingi hoova abil ning piirame seeläbi sirgjoonelise liikumise, võib keha veel ainult pöörelda ümber selle telje.
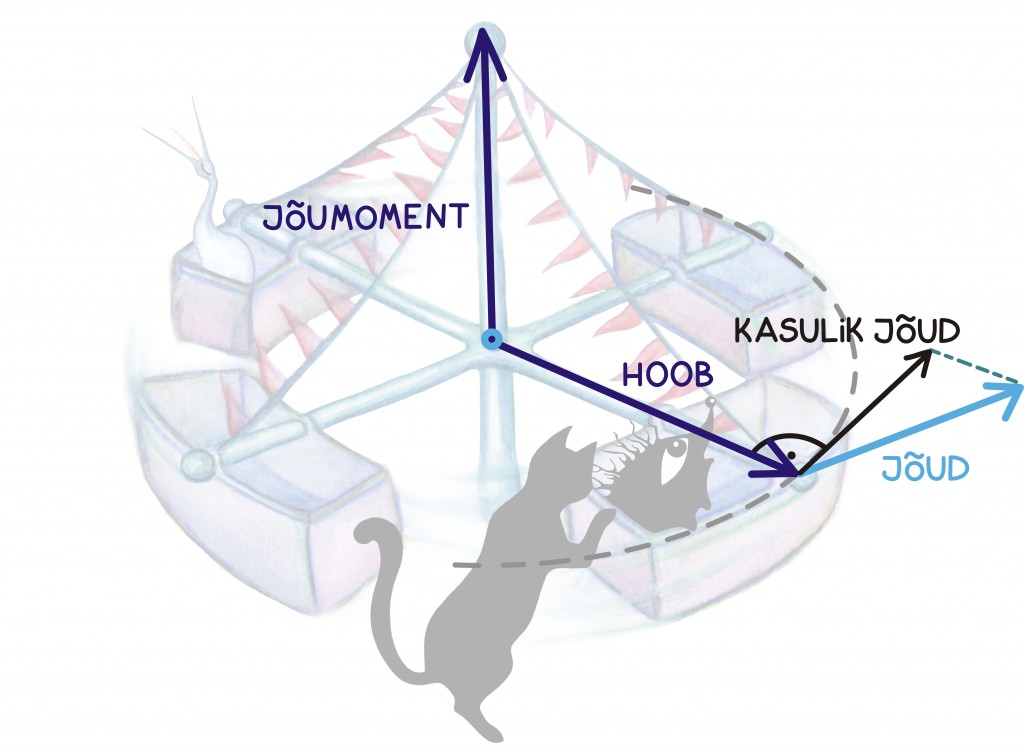
Keha pöörlemiskiirust mõjutab sel juhul hoopis hoovaga ristsuunaline jõukomponent, mida võib siis seekord kasulikuks jõuks nimetada. Kõige mugavam on pöörlema panevat mõju kirjeldada niinimetatud jõumomendi abil, milleks ongi täpselt hoova defineeriva vektori (füüsikute keeles: jõu mõjumispunkti tõmmatud kohavektori) ja kehale mõjuva jõuvektori vektorkorrutis.
Nagu jooniselt näeme, on jõumomendi näol tegemist mingi üsna kummalise vektoriga. Järgnevalt üritamegi selgitada, kuidas on vektorkorrutis ja seega ka jõumoment defineeritud ning miks just nii.
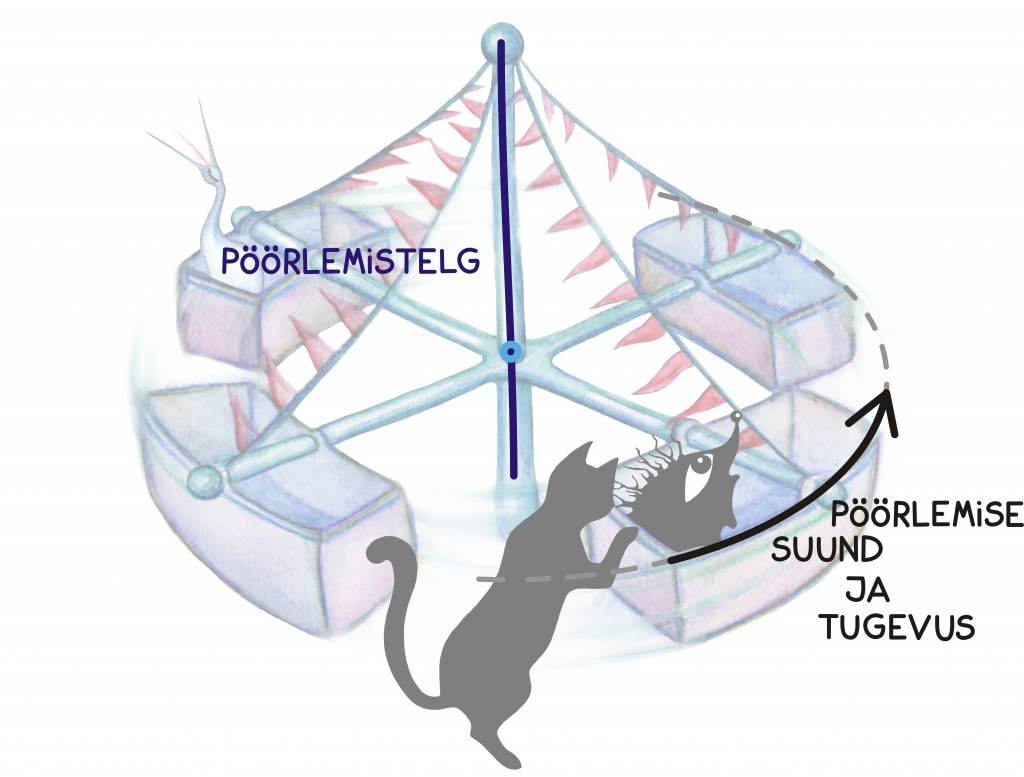
Alustame pöörlemise kirjeldamisest. Määratud sihis, näiteks sirgjoonelisel liikumisel mõjuva jõu kirjeldamiseks on vaja ainult ühte arvu – mõju suund on ju teada. Samas, pöörlemisse panustava mõju kirjeldamine on juba keerulisem, sest pöörlemine ise on pisut keerulisem liikumine. Kõige loomulikum on pöörlemist kirjeldada: 1)pöörlemistelje, 2) pöörlemissuuna ja 3) pöörlemiskiiruse või -tugevuse abil.
Need kõik kolm peavad olema seega peidetud ka jõumomendi kirjeldusse ehk jõu ning hoova vektorite vektorkorrutisse.
Seetõttu ongi vektorkorrutise tulemuseks uus vektor, mille suund annab meile pöörlemistelje, mille siht annab meile pöörlemise suuna ning mille pikkus määrab pöörlemise kiiruse.
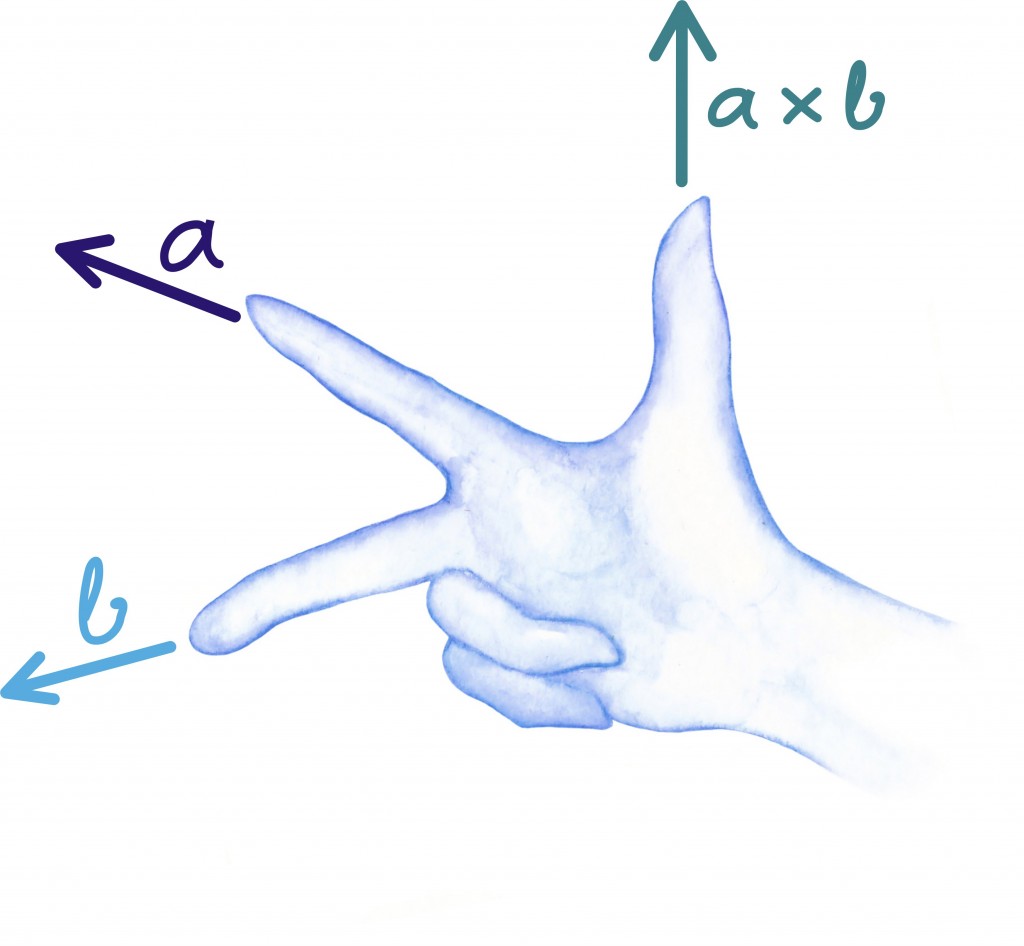
Sihi valikuks on meil kaks võimalust – kokkuleppeliselt toimub pöörlemine vastupäeva ümber pöörlemistelje sihi. Sellest kokkuleppest tuleneb ka nii-öelda parema käe reegel.
Kui skalaarkorrutise korral leidsime tema suuruse vektorite samasuunaliste komponentide korrutisest, siis vektorkorrutise suuruse leiame ristkomponentide abil. Vektorkorrutise suuruseks on
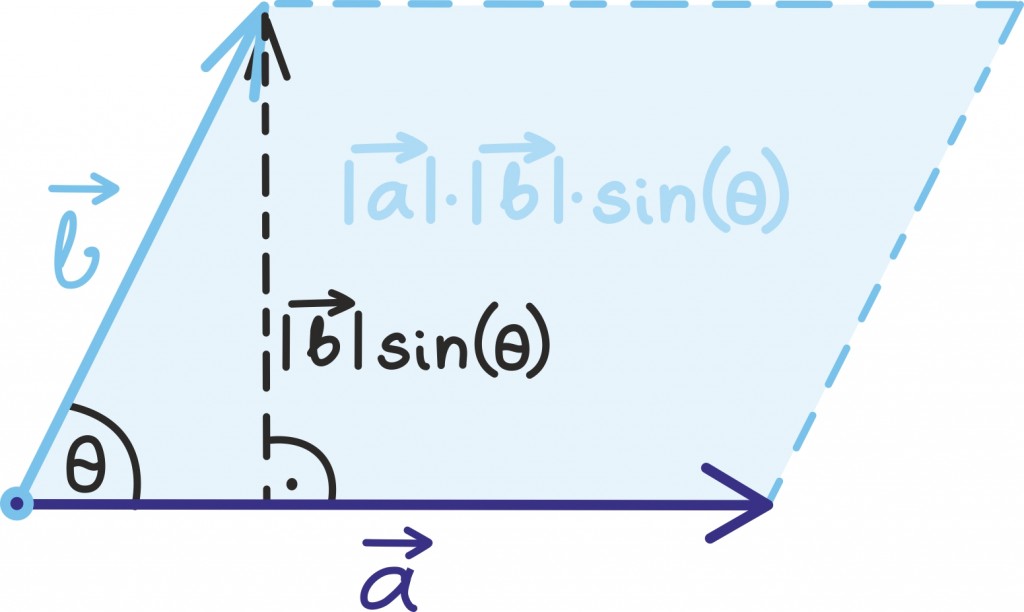
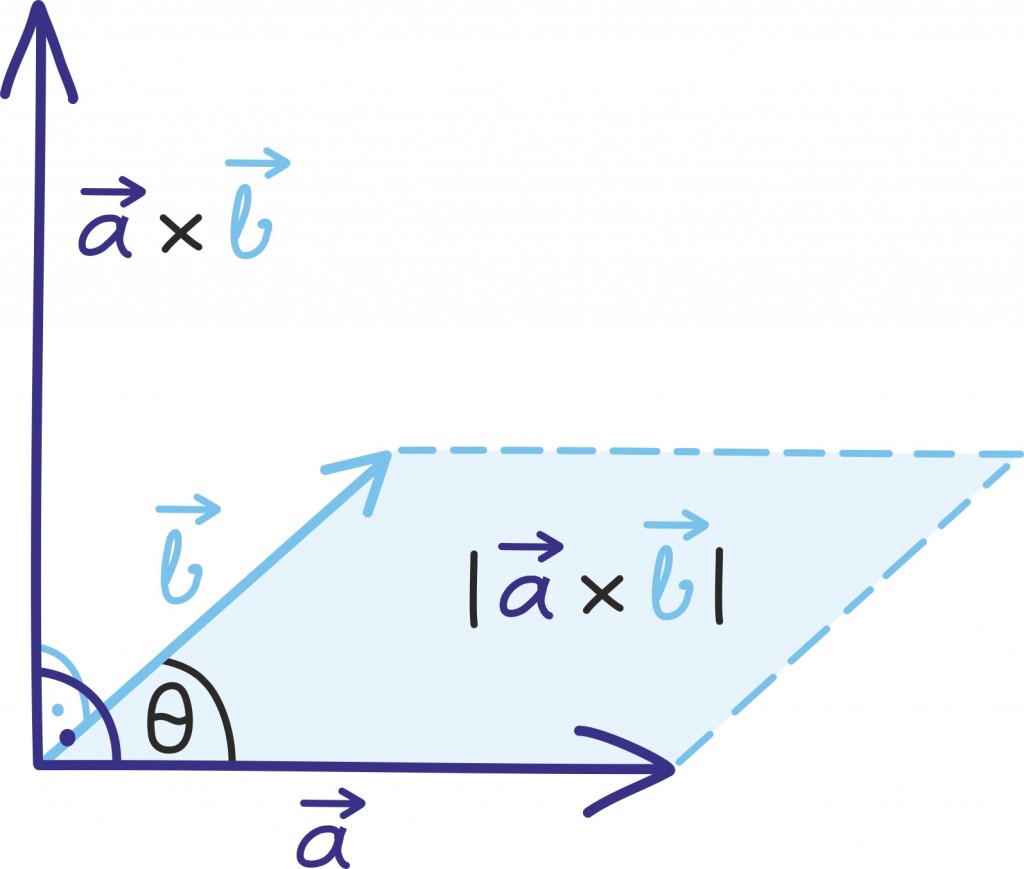
Seega, mida enam „risti” on kaks vektorit, seda suurem on ka nende vektorkorrutis. Nagu jooniselt näeme, on sellele suurusele ka kena tõlgendus: ta on võrdne kahe vektori poolt määratud rööpküliku pindalaga. Tõepoolest, võime mõelda, et  annab meile rööpküliku aluse,
annab meile rööpküliku aluse,
rööpküliku kõrguse ja pindala leiame nende korrutisest [lk 366]. Selle pindalade põhise tõlgenduse tõttu on vektorkorrutis seotud ka determinantidega, millest räägime maatriksite peatükis [lk 152].
Kokkuvõtlikult on vektorkorrutise tulemina saadud vektor risti mõlema vektoriga ning tema pikkus on võrdne esialgsete vektorite poolt moodustatud rööpküliku pindalaga. Kõike seda võib meelde jätmiseks ette kujutada järgmisel joonisel.
Lisaks jõumomendile aitab vektorkorrutis kirjeldada ka muud pöörlemisega seotut – näiteks pöörlemisimpulssi –, aga ka elektromagnetväljas toimuvat: näiteks magnetväljas liikuvale laengule mõjuv jõud on võrdeline tema kiirusvektori ning magnetväljavektori vektorkorrutisega.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!