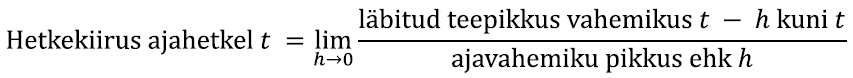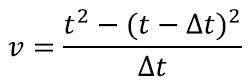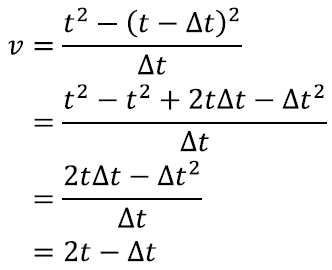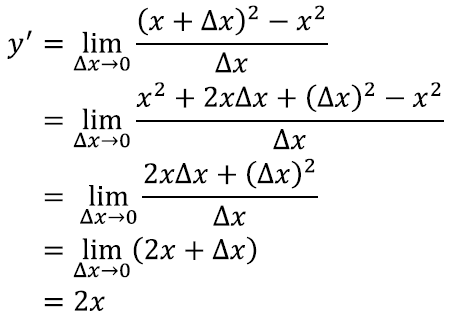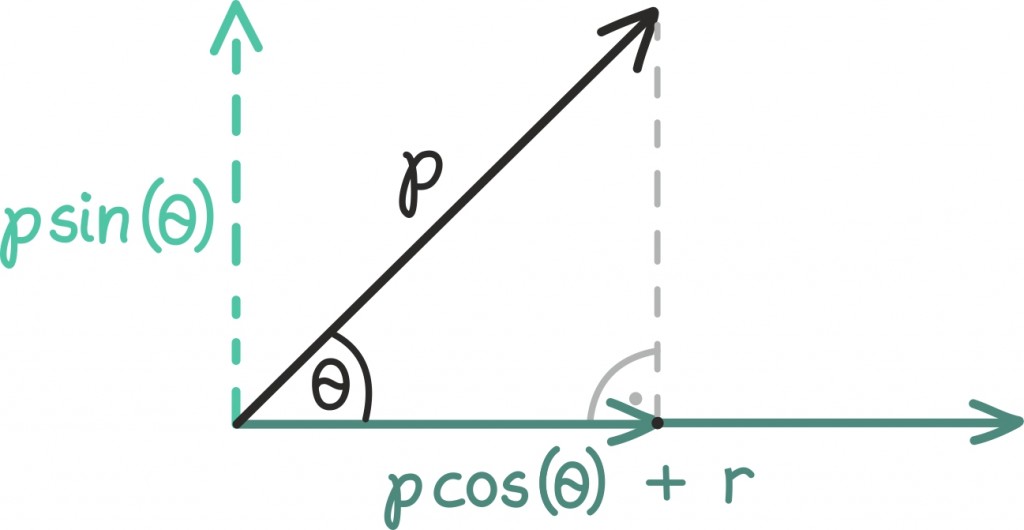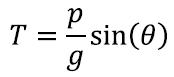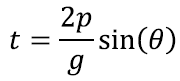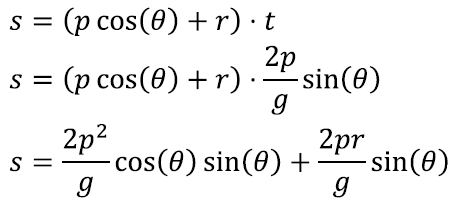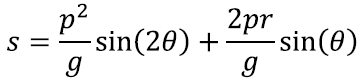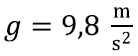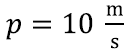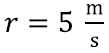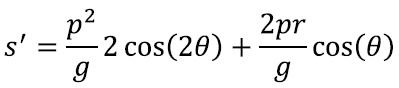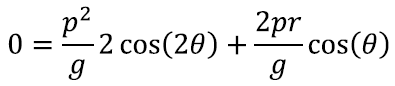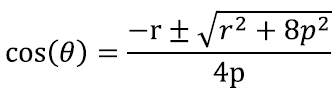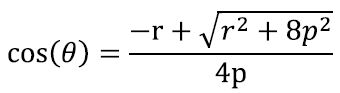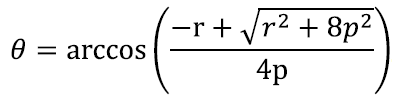Tuletis
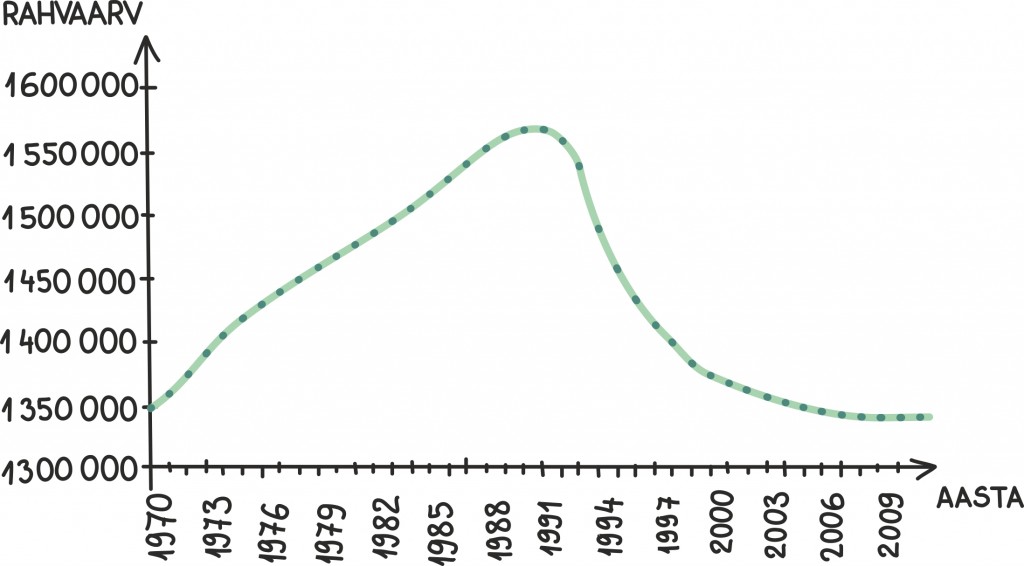
Rahvaarv on riigi seisukohalt tähtis näitaja – ta mõõdab mõne rahva suurust ja vägevust, meie puhul küll vist pigem väiksust ja haavatavust. Siin on viimase poole sajandi Eesti rahvaarvu graafik:
Rahvaarvu suurus määrab selle, kui palju riik makse koguda saab ja kui paljude kodanike eest on vaja hoolt kanda. Nii ei piisa meile lihtsalt rahvaarvu teadmisest, vaid tuleb ka aru saada, kuidas rahvaarv muutub.
Kas pole põnev, kuidas rahvastiku kasvamise üleminek kahanemiseks langeb kokku Eesti riigi taastekkimisega? Või see, et kuigi nüüdseks on rahvastiku kahanemine aeglustunud, pole kasv siiski veel taastunud? Veel näeme, et 1970-ndate alguses paistab kasv olevat olnud kõige kiirem. Miks just siis?
Rahvastiku muutumisest parema ülevaate saamiseks oleks kaval joonistada rahvaarvu muutumise graafik. Kui soovime näha, kui mitme inimese võrra rahvaarv aasta jooksul muutus, siis võiksime iga aasta rahvaarvust lahutada eelneva aasta rahvaarvu.
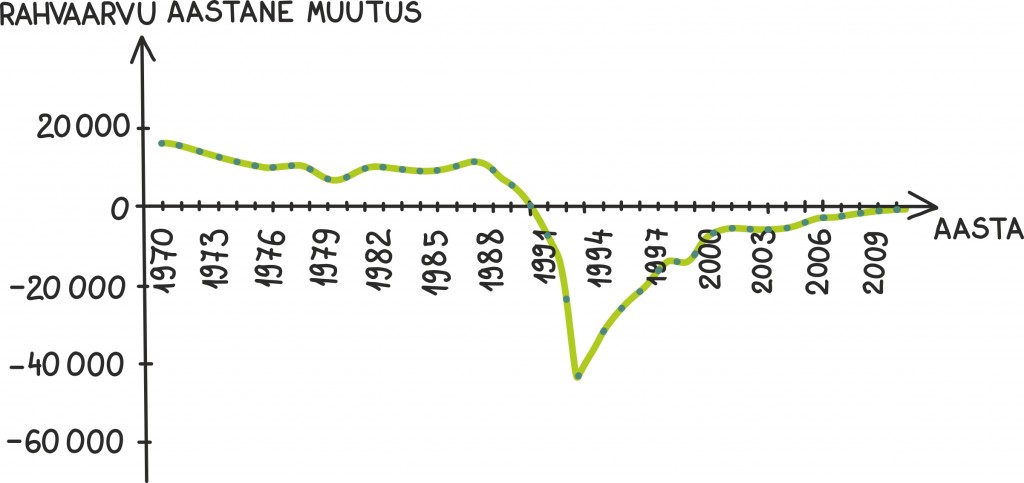
Kui teeme seda iga aasta kohta ja tõmbame saadud punktidest läbi ilusa joone, saame sellise graafiku:
See graafik ongi juba peaaegu rahvaarvu kirjeldava funktsiooni tuletise graafik! Tuletis annab meile ühe funktsiooni muutumise kiiruse igas punktis, täpsem definitsioon on küll pisut keerukam.
Lisakeerukus tuleneb sellest, et rahvaarvu puhul peame muutumise kiiruse leidma mingite ajavahemike abil, nagu aasta või kuu või nädal – liiga lühikeses ajavahemikus (näiteks üks nanosekund) ei juhtu ju tihti midagi. Lisaks peame valima, kas vaatame muutust lähitulevikus või lähiminevikus. Matemaatikas juhtub aga kogu aeg midagi ja nii kirjeldab tuletis funktsiooni väärtuse hetkelist muutumise kiirust – muutumist, mis toimub kiiremini kui mistahes nano- või pikosekund ja seda nii mineviku kui tuleviku suunal.
Tuletise definitsioon
Tuletis on ajast sõltuva funktsiooni jaoks justkui spidomeeter – iga ajahetke kohta näitab ta funktsiooni muutumise hetkekiirust. Aga kuidas leida spidomeetri näitu, kui teada on ainult läbitud tee pikkus?
Vastates sellele küsimusele jõuame ka tuletise range definitsioonini, kõike seda ühe talvise loo saatel.
Sulle võivad huvi pakkuda need õppematerjalid:
Numbrilised seosed
Harjutusülesandeid matemaatika riigieksamiks
Liitmine ja lahutamine 20 piires
Ruutvõrrand
Ratsionaalavaldised
Liitmine 10 piires
II kooliastme matemaatika reeglite kordamine
xy-koordinaatsüsteem
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine I kooliastmele
Kirjalik lahutamine
Algebralised murrud
Ruumilised kujundid
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonid ja nende graafikud
Funktsioonide graafikud
Üksliikmed, hulkliikmed ja tehted nendega
8. klassi matemaatika teooriavideod
Lahutamine 20 piires
Peastarvutamine eelkoolile
Talvine lugu
Kujutle, et oled metsa vahel suusatades jõudnud kõrgele mäe otsa ning võid nüüd hakata vabakäigul alla kihutama. Sind huvitab väga, kui suur on Su kiirus näiteks kümnendaks sekundiks. Kuidas võiksid seda hinnata?
Üks võimalus oleks lihtsalt mõõta, kui kaugele oled kümnendaks sekundiks jõudnud ning kaua see aega on võtnud. Jagades tee pikkuse ajaga, võiksid leida esimese kümne sekundi keskmise kiiruse ning selle abil oma kiirust ka kümnendal sekundil hinnata. Kogemuse põhjal aga teame, et kiirus kasvab päris hoogsalt ning ilmselt see poleks eriti hea hinnang.
Täpsema hinnangu saaksid aga näiteks siis, kui teaksid, kui kaugele oled jõudnud ka viiendaks sekundiks. Võiksid oma kümnenda sekundi kiirust hinnata vahemikus viiendast kümnenda sekundini toimunud laskumise keskmise kiirusena. Kui aga teaksid, kaugele oled jõudnud üheksandaks sekundiks, võiksid vaadata, palju läbisid veel viimasel sekundil, ning vastus oleks veelgi täpsem. Ja nii edasi – kui teaksid oma läbitud tee pikkust 9,99-ndal sekundil, oleks Su vastus juba peaaegu sama täpne nagu GPS-il. GPS-gi peab ju kiiruse kuidagi arvutama!
Leitud kiirus läheb järjest lühemat ajavahemikku kasutades aina täpsemaks, ent mis on see täpne vastus? Täpse vastuse nimi ongi tuletis ehk hetkekiirus. Kui tahame teda leida, peame keskmise kiiruse leidma järjest väiksemate vahemike jaoks ning lootma, et lõpuks koorub välja üks kindel vastus.
Sellist järjest väiksemate vahemike uurimist nägime eelmises peatükis piirprotsesside all. Tuletis ongi määratud piirprotsessiga [lk 313]: tuletis teatud hetkel on võrdne keskmise kiiruse piirväärtusega, kui uuritava ajavahemiku pikkus muutub olematult väikeseks. Matemaatilistes sümbolites tähendab see järgmist:
Konkreetne näide
Praktikas on küll hetkekiiruse leidmine võimalik ainult juhul, kui oma liikumist juba kuidagi matemaatiliselt kirjeldame – on ju võimatu, et leiame tee pikkuse iga nanosekundi tagant. Ise mõõtes jääme alati lähendusteni.
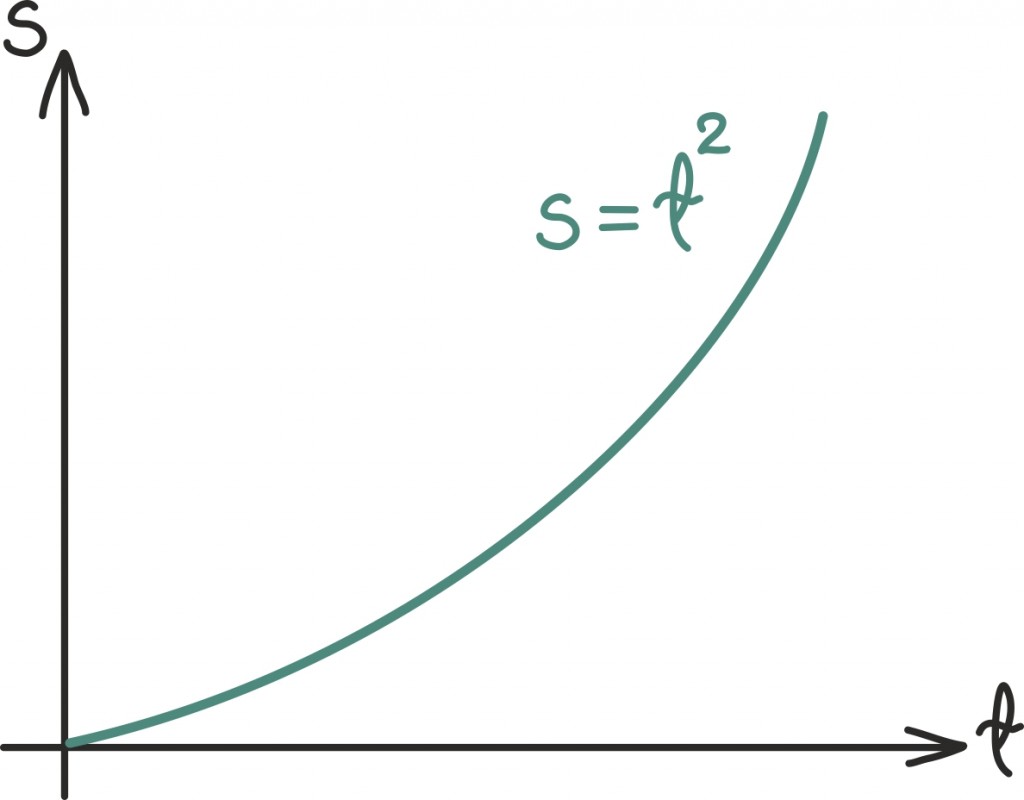
Täpsuseni aitab meid aga näiteks füüsika. Mäest alla sõitu võime füüsikatunni tarkuse abil lihtsalt matemaatiliselt kirjeldada. Nimelt kui kallak on ühtlase nurga all, kui hõõrdejõu, liikumisele vastu võitleva tuulejõu ja muu tühja-tähja ära unustame ning kui alustad mäe otsast nullkiirusega, siis on laskumisel läbitud tee pikkus antud ruutfunktsiooniga ajast: kujus ct2.
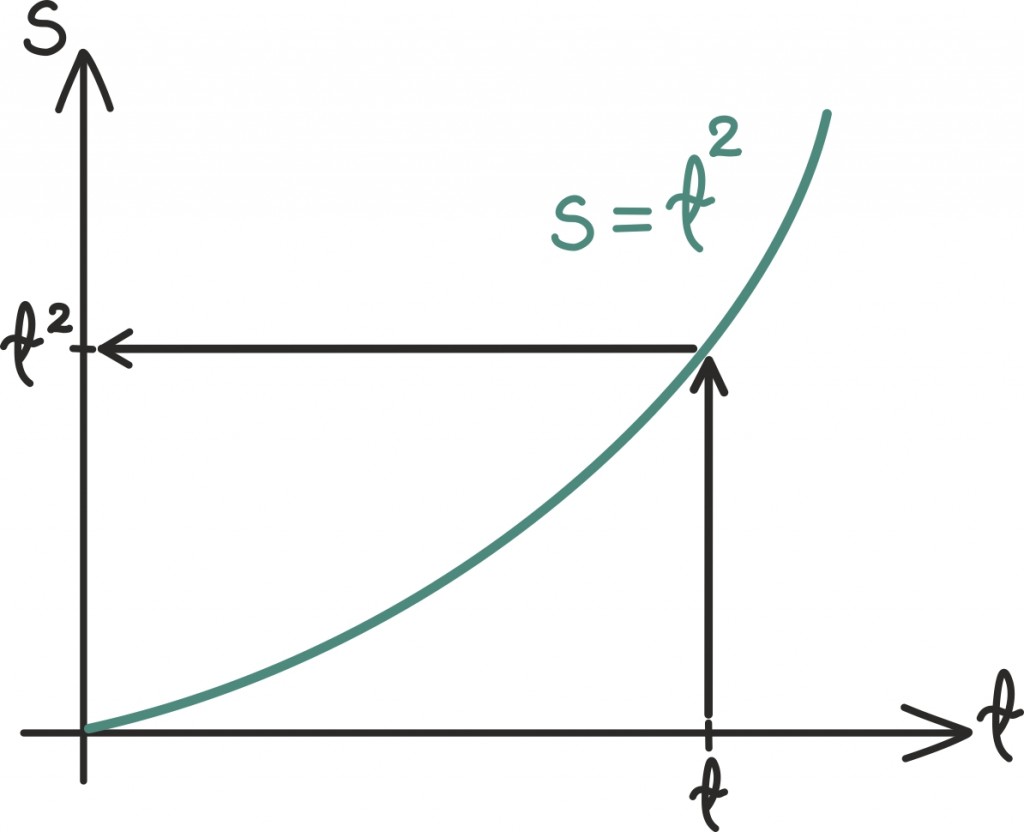
Konstant c peaks olema konkreetne reaalarv, mis sõltub gravitatsioonikonstandist ja kaldenurgast, aga lihtsuse huvides ütleme, et valisid kõige ilusama mäe siin maailmas ning c = 1. Sel juhul saame läbitud tee pikkuse funktsiooniks s = t2 ehk näiteks 10 sekundit pärast laskumise algust oled jõudnud 100 meetri kaugusele.
Selle valemi põhjal võime nüüd kergesti leida ka oma hetkekiiruse. Kusjuures enam ei ole vahet, kas teeme seda ainult 10 sekundi või iga üldise ajahetke t jaoks. Lühikese ajavahemiku pikkust kirjeldame sümboliga Δt, aga nagu ikka on see kokkuleppeline.
Teame, et suvalisel ajahetkel t oleme jõudnud t2 meetri kaugusele.
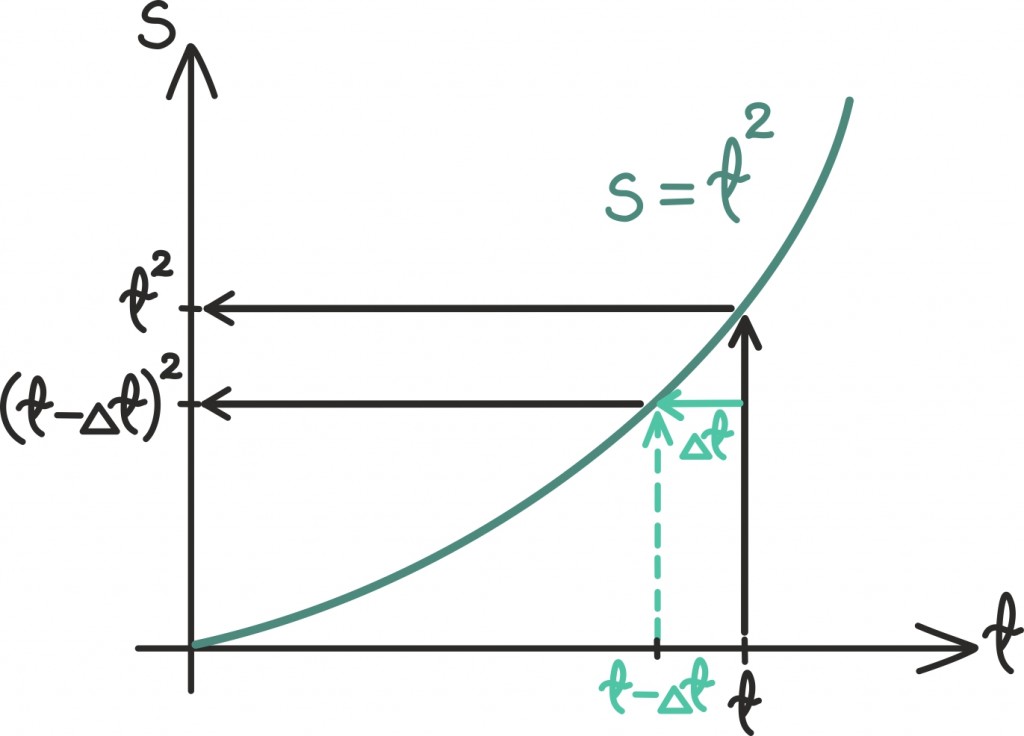
Ajahetkeks t – Δt oleme samas jõudnud (t – Δt)2 kaugusele:
Nüüd on meil olemas kõik keskmise kiiruse leidmiseks ajavahemikus t – Δt kuni t:
Edasi võime saadud valemit pisut lihtsustada. Korrutades ruudus oleva liikme lahti, koondades sarnased liikmed ning taandades murru, saame järgmise hinnangu:
Märkame, et ajavahemiku pikkus Δt mõjutab üsna selgelt meie kiiruse hinnangut. Samas, kui muudame selle ajavahemiku järjest väikesemaks, kahaneb tema mõju järjepanu. Viimaks on ta nullist päris eristamatu ning alles jääbki ainult 2t. Järelikult funktsiooni t2 muutumise hetkekiirus ehk tuletis suvalisel hetkel t on v = 2t.
Seega meie füüsikalise kirjelduse põhjal suureneb sellest ideaalsest mäest alla lastes laskumiskiirus iga sekundi kohta 2 m/s võrra. Seega näiteks viiendal sekundil on kiiruseks 10 m/s ning kümnendal sekundil juba 20 m/s ehk üle 70 km/h – kui kiirust kardad, ära pikka laskumist ette võta.
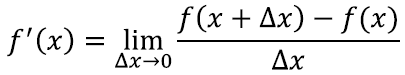Märkame, et kui lugulaulus defineerisime tuletise ühel kohal argumendist vasakule jäävate vahemike abil, siis nüüd nõuame muutumise vahemikult Δx ainult seda, et ta koonduks nulli. Ta võib olla nii positiivsete (tulevikku vaatav), negatiivsete (minevikku vaatav) kui vaheldumisi väärtustega. Nagu hiljem näeme, on selline üldisus oluline, et võiksime tuletisest üheselt rääkida.Eelneva arutluskäigu funktsiooni y = x2 tuletise leidmiseks võiks seetõttu kompaktselt kirja panna ka tulevikku vaatavalt:
Tore, et vastus on sama!
Igaks juhuks mainime, et tähistused ƒ'(x) ja y‘ tähendavad täpselt sama asja. Tihti tähistatakse reaalarvulisi funktsioone y abil, sest meile meeldib ju funktsiooni graafikuid joonistada x– ja y-telje abil. Sel juhul unustatakse tihti üldse märkida, et argumendiks on x – seda loetakse vaikimisi teadmiseks. Vahel nimetatakse funktsioone ƒ(x)-ks, kuna ƒ on ju sõna funktsioon esimene täht. Siis märgitakse segaduse vältimiseks ka ära, et funktsiooni argumendiks on ikkagi just nimelt x. Märgi ‘ võttis tuletise tähistamiseks alles 18. sajandi lõpus kasutusele itaallane J.L. de Lagrange.
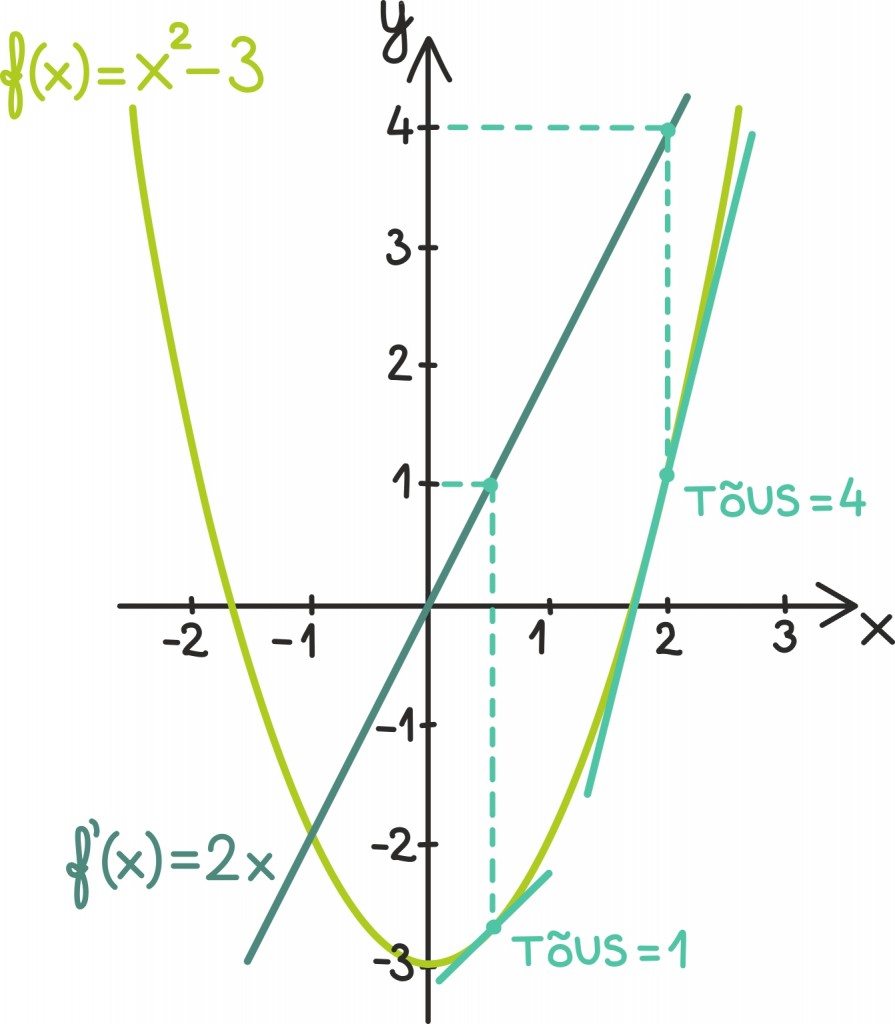
Tuletise geomeetriline tõlgendus
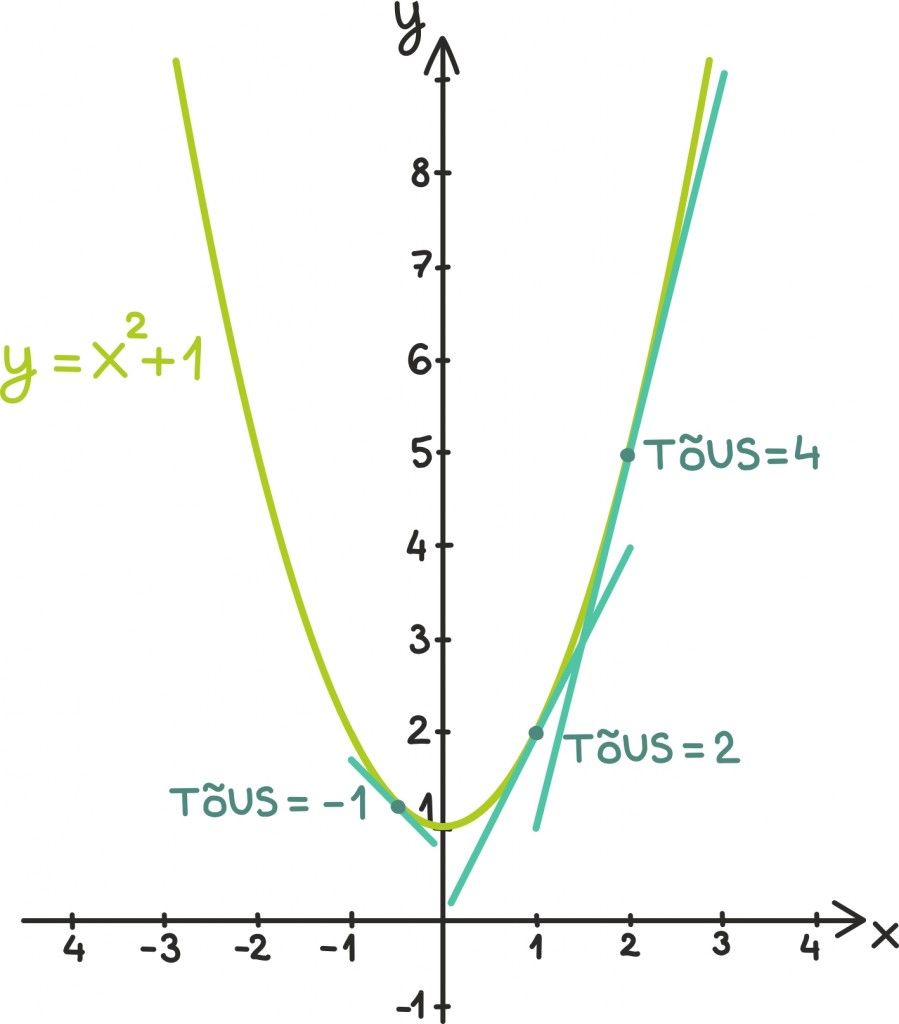
Funktsiooni tuletisest saab mõelda ka funktsiooni graafikule tõmmatud puutujasirgete abil. Nimelt on funktsiooni tuletis igas punktis võrdne seal punktis funktsiooni graafikut puudutava sirge tõusuga.
Miks see peaks nii olema? Keskmise kiiruse idee ise on juba seotud sirge tõmbamisega: selle asemel, et uurida, kuidas tee pikkus detailselt muutub, võtame ajavahemiku otspunktid ning ühendame need sirgega. Selle sirge tõus on siis ka selle vahemiku keskmine kiirus.
Tuletise leidmiseks teeme aga ajavahemiku lõpmatult väikeseks ehk teisisõnu muudame ajavahemiku ots- ja alguspunkti samaks: nii saab sirgest puutujasirge.
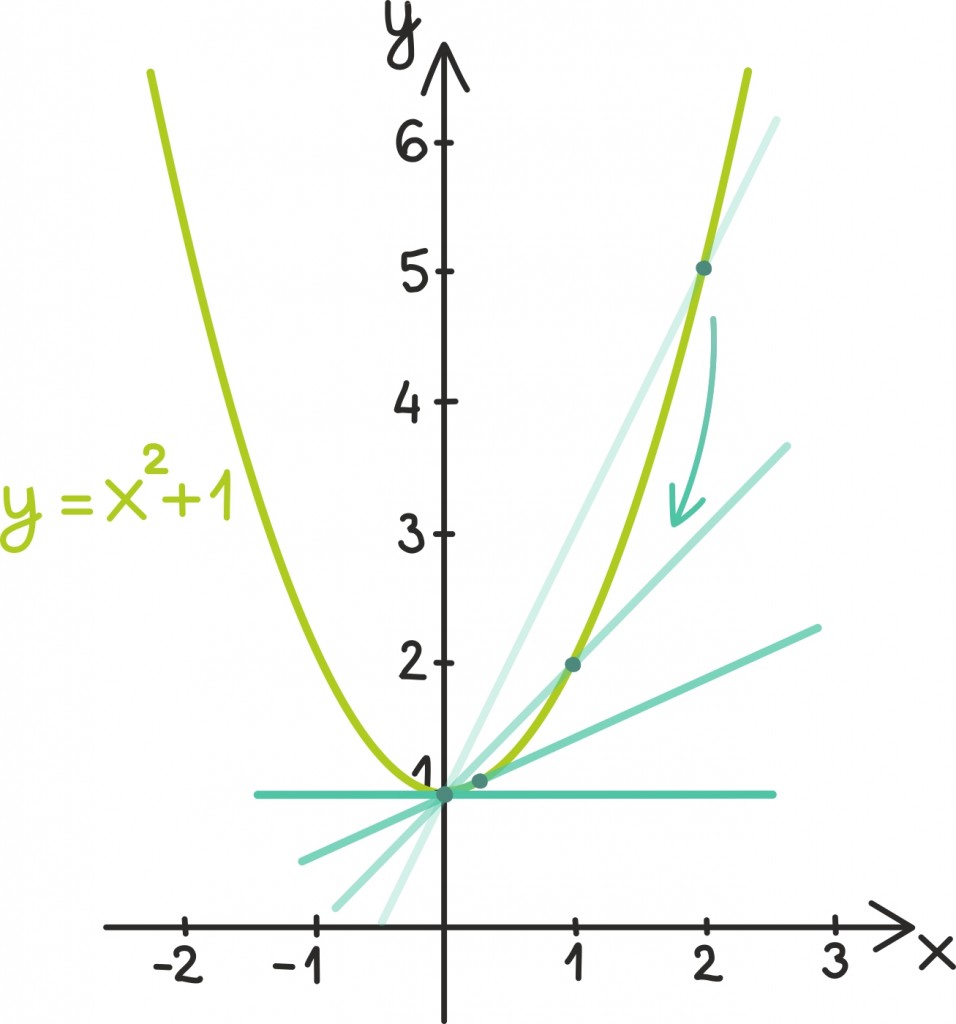
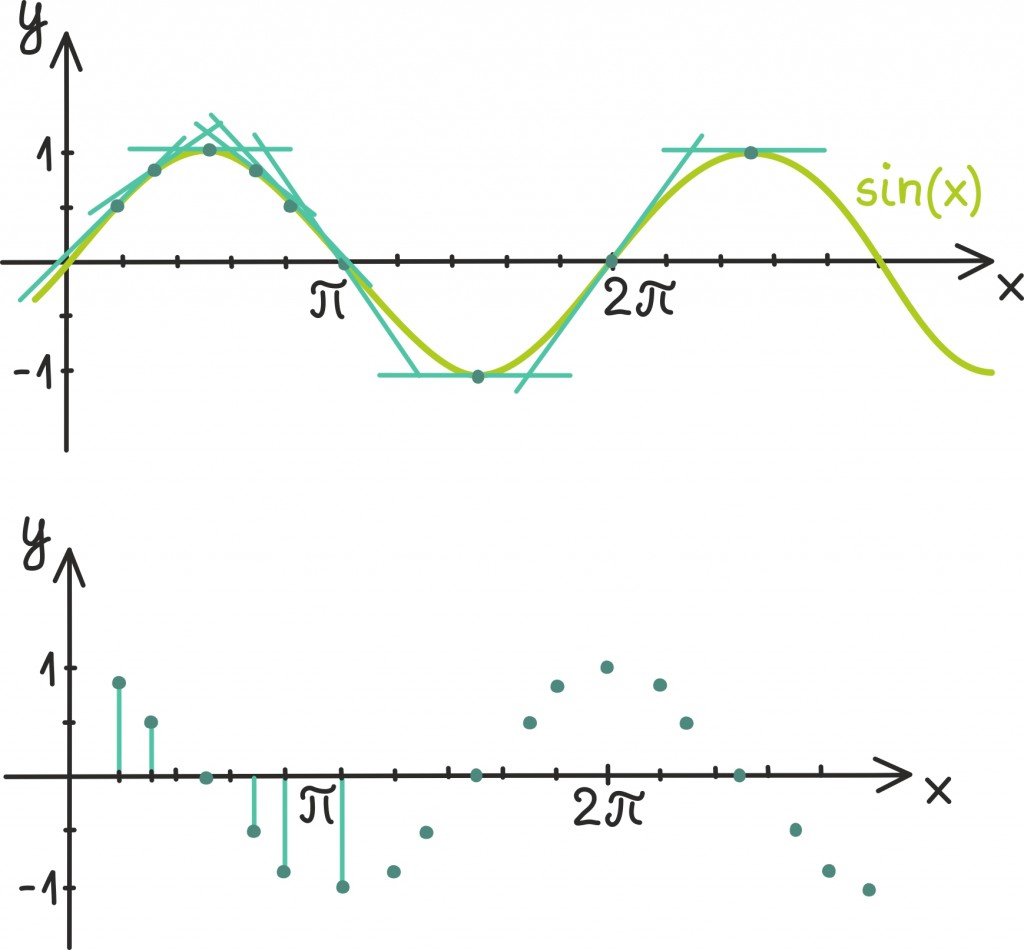
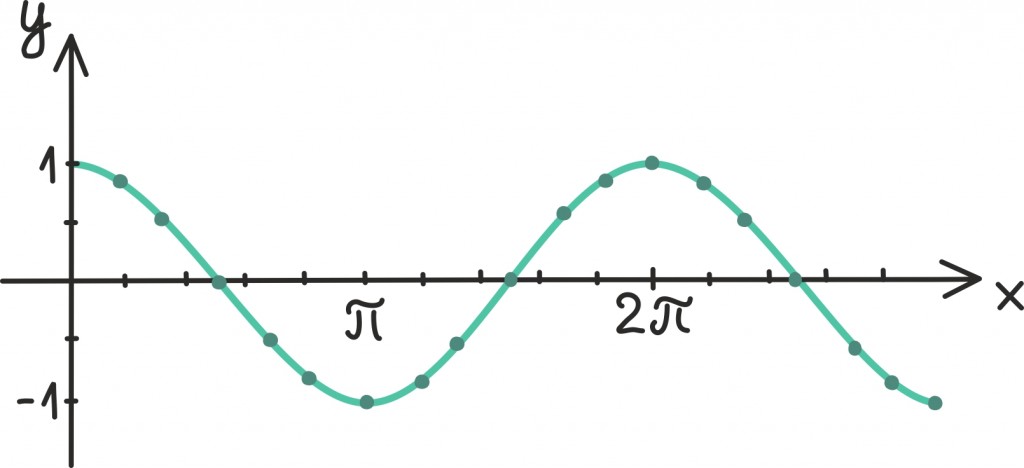
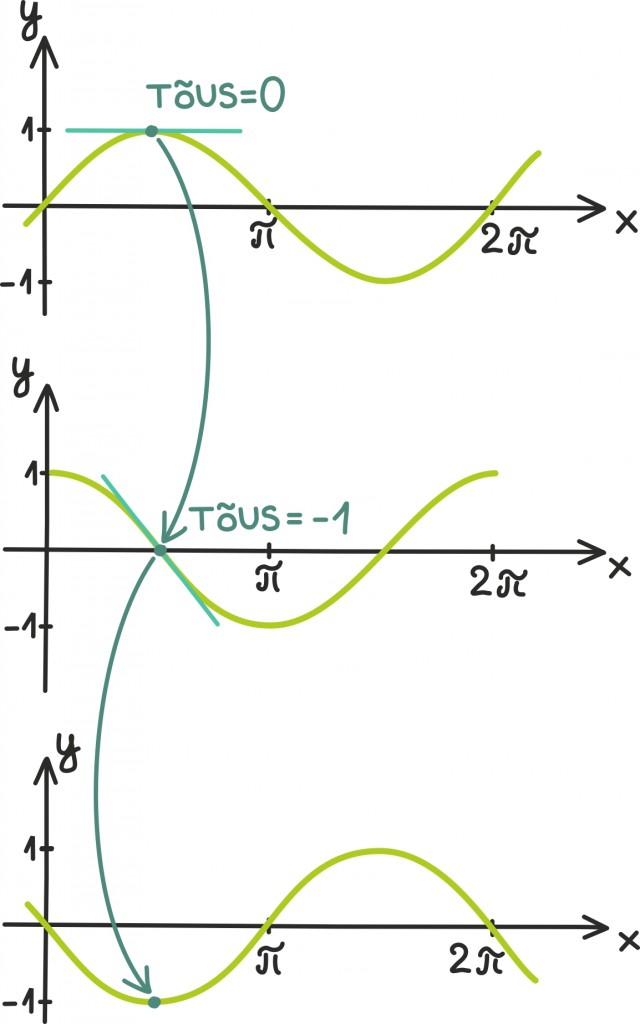
Vaatame näitena veel siinusfunktsiooni graafikut, mille abil saab kirjeldada paljusid perioodilisi protsesse, sealhulgas näiteks ka pendli liikumist [lk 236]. Tõmbame siinusfunktsiooni graafikule lahkesti erinevaid puutujasirgeid:
Nende puutujasirgete tõusudest uut joonist tehes näeme, et see ei paista eelmisest sugugi väga palju erinevat – ainult nihutamise võrra. Natukene mälus sobrades leiame, et saadud joonis sarnaneb väga koosinusfunktsiooni graafikule:
Tõepoolest, tulebki välja [lk 251], et siinusfunktsiooni tuletis on koosinusfunktsioon ning koosinusfunktsiooni tuletis omakorda horisontaalteljest peegeldatud siinusfunktsioon. Seega on trigonomeetrilised funktsioonid üsna eraldihoidev pere.
Ekstreemumid
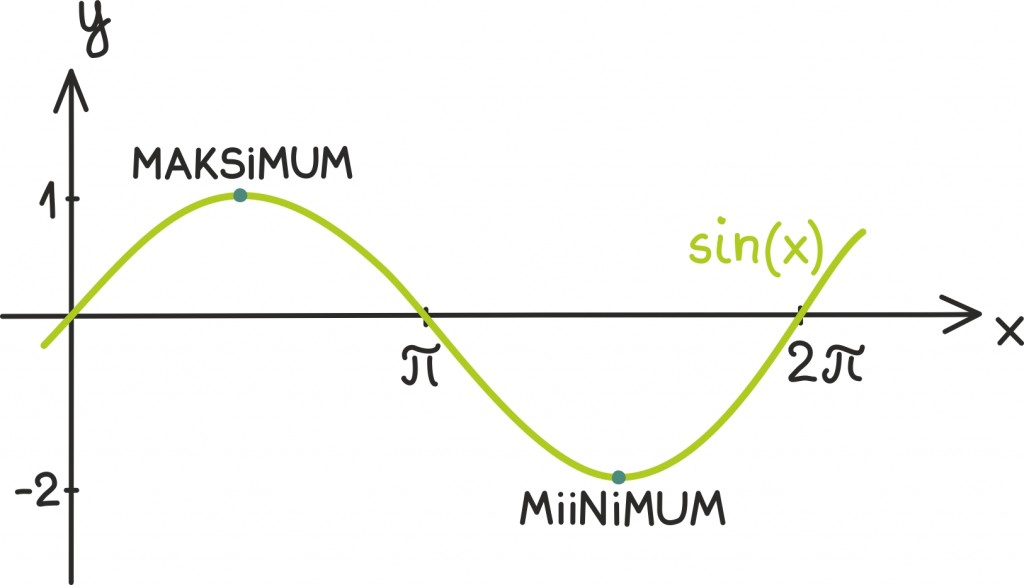
Graafiline mõtteviis aitab ka aru saada sellest, miks tuletise nullkohad on nõnda olulised. Nimelt näeme, et tuletis on võrdne nulliga täpselt kohtades, kus puutujasirge on paralleelne x-teljega – ehk teisisõnu kohtades, kus funktsioonil on kogu oma ümbrusest suurem või väiksem väärtus. Selliseid kohti nimetatakse ekstreemumiteks. Ekstreemumit, mis on mingil väiksel alal kõige suurema väärtusega, nimetatakse maksimumpunktiks ning madalamat punkti miinimumpunktiks.
Ekstreemumite uurimine on päris oluline, kuna tänapäeval on ikka kombeks kõike kas maksimeerida või minimeerida: majandusteadlased tahavad maksimeerida kasumit, vormeli-insenerid tippkiiruseid ja õpilased uneaega.
Kuidas see täpsemalt käib, räägime lahendades vägagi olulist probleemi näiteks tutipäevaks: mis nurga alt visata ratta seljast veepomme [lk 333]? Enne aga veel midagi pisut matemaatilisemat.
Millal tuletis eksisteerib?
Sissejuhatuses rääkisime rahvaarvu muutumisest – see oli tuletise kontekstis pisut eksitav, kuna rahvaarvu täpselt kirjeldavale funktsioonile ei saagi igal pool tuletist leida.
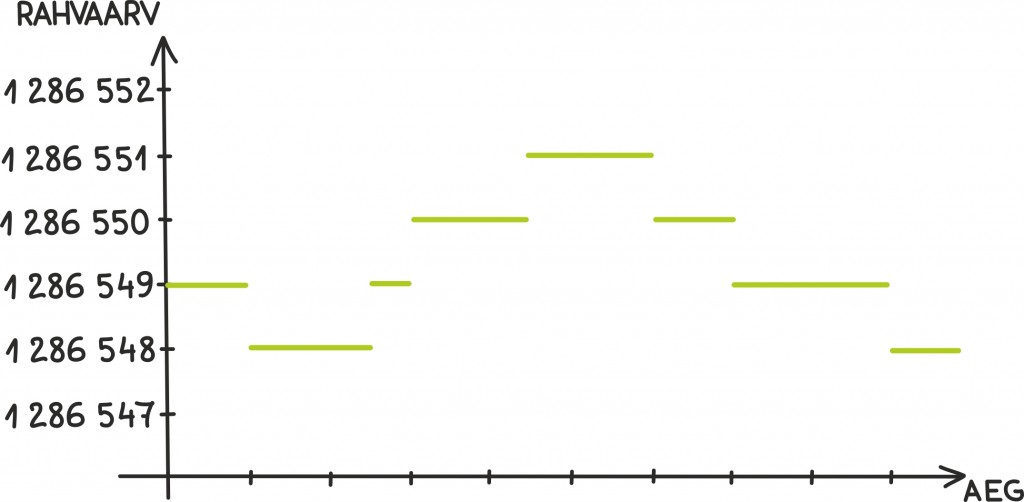
Nimelt, tegelikult ei ole ju rahvaarvu muutumine sugugi pidev protsess, vaid toimub konkreetsete juhtumite kaupa, keegi sünnib, keegi sureb. Nii meenutab rahvaarvu graafik sissesuumitult treppi:
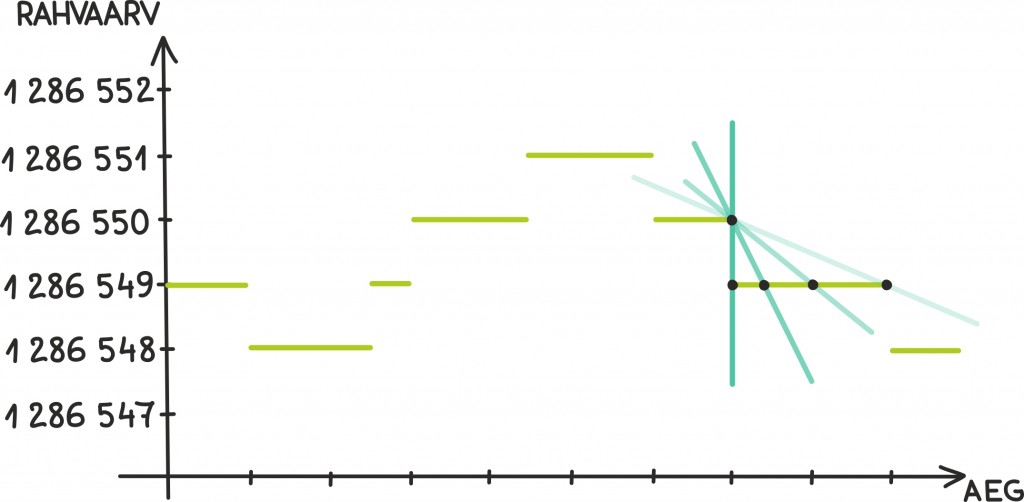
Seega on piisavalt väikesel ajavahemikul rahvaarvu muutus alati kas null või absoluutväärtuselt vähemalt üks – just on keegi sündinud või surnud. Esimesel juhul on tuletis null ning teisel juhul hoopis defineerimata. Tõepoolest, kui muutu ei ole üheski suunas, on tuletis definitsiooni järgi null. Teisalt, kui muut on aga ükskõik kui väikese ajavahemiku jaoks fikseeritud, siis ju keskmine kiirus vahemiku vähenedes aina kasvab või kahaneb ning jõuabki lõpmatusse. Kui see jäi segaseks, võib mõelda näiteks puutujasirgetele – hüppepunktis muutub ta ühe suunas hoopis vertikaalseks ehk tõus saab lõpmata suureks või väikeseks:
Seega ei kanna tuletis rahvaarvu muutuse kohta tegelikkuses eriti mingit teavet. Teda ei saa isegi igal pool ilusasti defineerida ning peame rahvaarvu uurimisel kasutama ebatäpsemaid hinnanguid, nagu tegime seda sissejuhatuses – peame uurima muutust ühe aasta, ühe kuu või muu lõpliku ajavahemiku vältel.
Nii mõnelgi teisel funktsioonil ei saa osades kohtades tuletist leida ja tuleb välja, et leidub lausa funktsioone, mis on küll pidevad, aga kus ei saa üheski kohas tuletist leida! Need on parajad monstrumid ning mõned neist meenutavad mõningal määral fraktaalset lumehelvest, mille kohta saab lugeda juba järgmisest osast [lk 377].
Ja isegi kui füüsikud tegelevad peaaegu alati funktsioonidega, millel tuletis leidub – nagu näiteks juba nähtud ruutfunktsioon või siinusfunktsioon – on oluline küsida, millal üldse on tuletisest mõistlik rääkida. Seda järgnevalt arutamegi.
Meenutame, et defineerisime funktsiooni tuletise mingil kohal piirprotsessi kaudu. Seega leidubki funktsiooni tuletis sellel kohal täpselt siis, kui sellel piirprotsessil tõepoolest leidub piirväärtus.
Seda tingimust veidi lähemalt uurides selgub näiteks, et iga funktsioon, millel leidub mingis punktis tuletis, peaks olema tingimata sealsamas punktis ka pidev. See oli täpselt probleem, mida kohtasime mõni lehekülg tagasi rahvaarvu kirjeldavat funktsiooni uurides – hüppekohale ei saa tuletist joonistada.
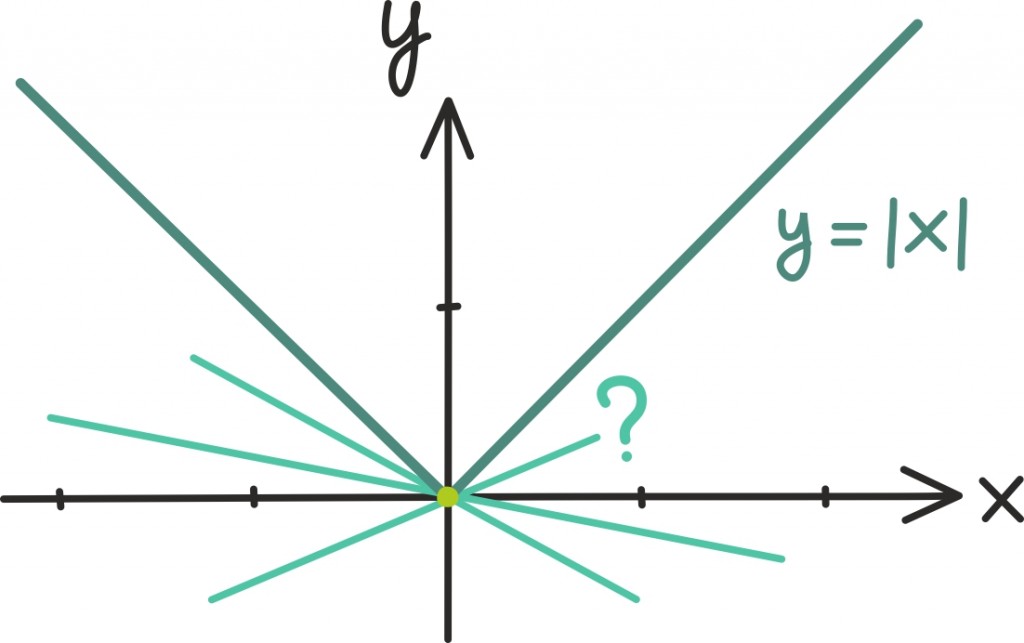
Tuleb välja, et tuletise olemasoluks ei piisa ka lihtsalt pidevusest – näiteks ei leidu absoluutväärtuse funktsioonil y = |x| tuletist punktist 0. Ka sellest on lihtne aru saada just geomeetriliselt. Teravikule on jällegi väga raske joonistada puutujasirget. Paremalt poolt lähenedes tundub, et puutujasirge peaks olema võrdne sirgega y = x, vasemalt poolt lähenedes sirgega y = –x. Kumma peaksime valima?
Või hoopis mõne keskmise? Ükski sirge ei kirjelda funktsiooni muutumist üheaegselt nii negatiivses kui positiivses suunas.
Üldiselt kehtib, et kui ühel funktsioonil leidub igas punktis tuletis, on ta konaruste ja teraviketa. Proovi ise – ainult siis saad igasse punkti joonistada üheselt puutujasirge. Puutujasirge olemasolu aga tähendab, et funktsioon muutub vähemalt imepisikeses piirkonnas üsna lineaarselt ehk sirgjooneliselt mõlemas suunas, umbes nii nagu kerajas Maa pind tundub koduümbruses igati lame.
Teine tuletis, kolmas tuletis jne
Tuletis on põnev, kuna oleme teatud mõttes asunud teisendama keerulisemaid objekte kui arve.
Kui ühel funktsioonil leidub igas punktis tuletis, siis võime tuletise võtmisest mõelda kui ühe funktsiooni teisendamisest uueks funktsiooniks: funktsioonist y = ƒ(x) saab tuletise võtmisel uus funktsioon, mida tavaliselt tähistatakse y‘ = ƒ'(x) ning mille väärtus igas punktis annabki algse funktsiooni tuletise väärtuse selles punktis.
Nüüd ka y‘ on funktsioon ning seega võime ju samamoodi uurida tema muutumist. Kui ta muutub piisavalt kenasti, võime võtta temastki tuletise ning saada funktsiooni y”. Kui nüüd omakorda funktsioony” on kena ning sile, võime leida veel kolmandagi tuletise ja nii edasi.
Funktsioonid, millest saame palju tuletisi võtta, on eriti sujuvad ja siledad. Heaks näiteks on jälle polünoomid või trigonomeetrilised funktsioonid siinus ja koosinus. Nagu mainisime, muutub siinusfunktsioon tuletist võttes koosinusfunktsiooniks ning koosinusfunktsioon x-teljest peegeldatud siinusfunktsiooniks. Nii võime tuletise võtmist lõputult jätkata:
ning
Nii saame näiteks pendli liikumist üsna täpselt kirjeldada kolme funktsiooniga: esiteks pendli kaugus nullpunktist, seejärel tuletis sellest funktsioonist ehk pendli liikumise kiirus ning viimaks tuletis kiirust kirjeldavast funktsioonist ehk pendli liikumise kiirendus.
Hoo pealt veepommi viskamine*
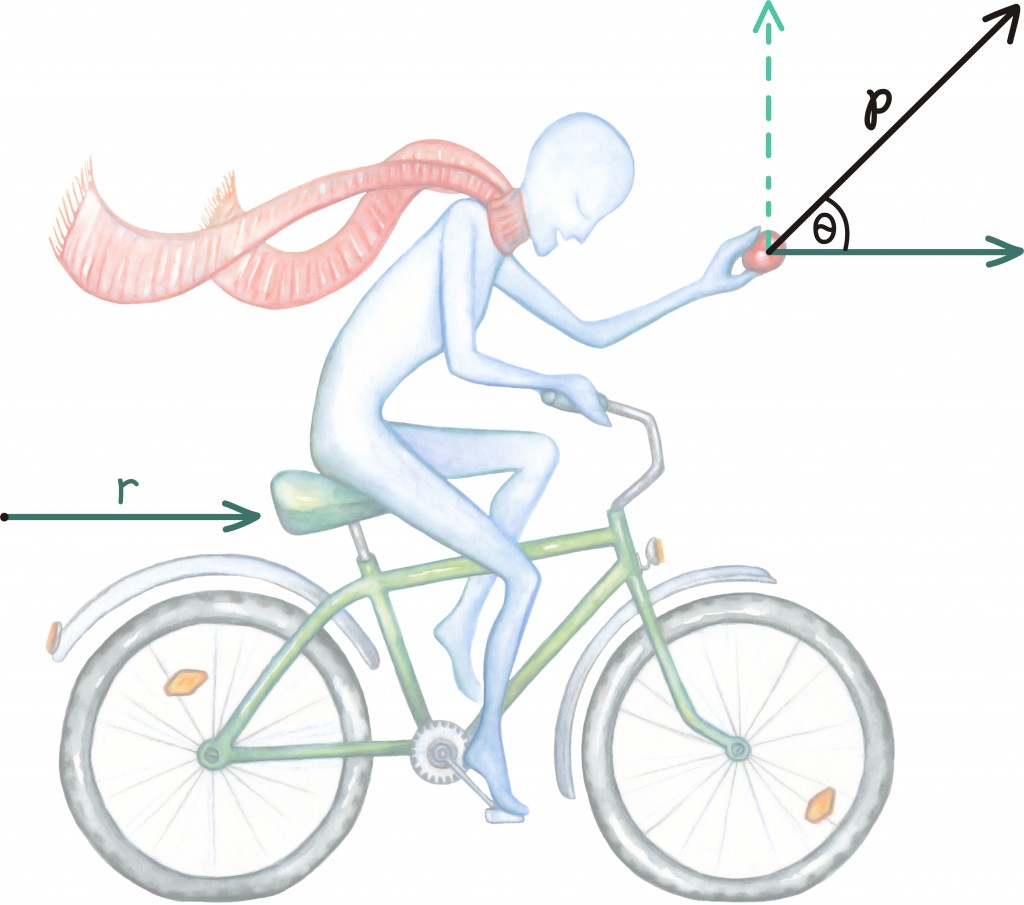
Oled gangsterifilmidest saanud natukene halba inspiratsiooni ja otsustad jalgrattalt veepomme pilduda. Mis nurga all peaksid viskeid sooritama, et veepommid võimalikult kaugele lendaksid?
Tänaseks on vist üsna levinud tarkus, et seisult on kõige kasulikum palli või ka veepommi visata täpselt 45-kraadise nurga alt. Aga kuidas muutub see nurk siis, kui sõidad samal ajal ratta või autoga või hoopis jooksed?
Järgnevalt üritamegi üheaegselt leida põhjendust rahvatarkusele ning arvutada ka välja parima nurga hoo pealt viskamiseks. Selle jaoks peame esiteks leidma olukorrale sobiva füüsikalise kirjelduse, seda veidi matemaatiliselt analüüsima ning siis järeldustesse ruttama. Seejuures tähendab analüüsimine siinkohal mingi optimaalse väärtuse leidmist ja mängu tulebki tuletis, mis võrdub nulliga just funktsiooni maksimumpunktis.
Füüsikaline kirjeldus
Hea füüsikalise kirjelduse aluseks on otsus, milliseid faktoreid veepommi viskel arvesse võtta ning mida eirata.
Veepommi langemist põhjustab gravitatsioonijõud, nii et sellest me loobuda ei saa. Tähistame gravitatsioonijõust tulenevat kiirendust tähega g. Samuti mängivad kindlasti rolli jalgratta kiirus ning veepommile meie poolt antav algkiirus. Kuna nende täpseid väärtuseid me ei tea, tähistame ratta kiirust tähega r ning palliviske kiirust tähega p. Viimaks on oluline muidugi otsitav viskenurk ise – tähistame teda θ-ga.
Selline üldkujus lahendamine võimaldab meil ka hiljem proovida, kuidas vastus sõltub näiteks sõidu- või viskekiirusest.
Kõike muud aga otsustame esmajoones eirata – kui veepomm on piisavalt kompaktne, siis tuuletakistus ei tohiks liialt suurt rolli mängida. Samuti näiteks eirame fakti, et vise ei toimu päris maapinnalt, vaid veidi kõrgemalt.
Newtoni teise seaduse põhjal võime keha liikumist kirjeldada temale mõjuvate jõudude abil – ainult jõudude mõjumisel muutub ka keha liikumise kiirus. Kõnealuses olukorras on meil ainult üks jõud, gravitatsioonijõud, mis mõjub vertikaalselt allapoole. Horisontaalselt ei mõju ühtegi jõudu ning seega jääb horisontaalkiirus ka terve lennu ajal samaks.
Võime need kiirused ka trigonomeetriliste funktsioonide abil kirja panna:
Horisontaalkiirus on konstantselt
Vertikaalkiirus on algselt antud
hakkab seejärel tänu gravitatsioonijõule vähenema, kuni jõuab nulli (kõrgeim punkt!), ning seejärel jälle suurenema, kuni veepomm prantsatab maapinnale.
Just selle vertikaalkiiruse kirjelduse abil saame leida ka lennuaja.
Leiame esmalt lennuaja, mis kulub veepommi tõusmiseks kuni kõrgeima punktini. Teame, et vertikaalkiiruse tuletis ehk kiirendus on ülesviskel võrdne g-ga. Seega võime kiiruse ajahetkel t kirjutada kujus:
Kõrgeimas punktis on vertikaalkiirus täpselt null ning saame võrrandi tõusmiseks kulunud aja T suhtes:
Siit võime avaldada üleslennule kulunud aja:
Natuke mõeldes selgub, et ka allalennule kulub täpselt sama aeg. Üks viis selles veendumiseks on kasutada energia jäävuse seadust. Nii viske kui maandumise hetkel peab palli koguenergia olema sama. Kuna potentsiaalne energia on neil hetkedel võrdne ning samuti ka horisontaalne kiirus, peavad suuruselt võrdsed olema ka vertikaalsed kiirused – ainult vastupidises suunas. Seega langemisel muutub vertikaalkiirus sama palju nagu tõusmisel. Kuna kiiruse muudu määrab endiselt ainult raskuskiirendus, kulub ka kiiruse muutumiseks täpselt sama aeg.
Seega peame kogu lennuaja leidmiseks korrutama tõusule kulunud aja kahega. Tähistades kogu lennuaega lihtsalt t-ga, saamegi:
Nüüd võime horisontaalkiiruse abil leida ka viske pikkuse. Kuna horisontaalses suunas on kiirus konstantne, peame selle jaoks lihtsalt korrutama kiiruse ning ajapikkuse.
Saame:
Kasutades siinusfunktsiooni topeltnurga valemit [lk 245]
saame seda veel veidi lihtsustada:
Ikkagi päris õudne valem! Vähemalt näeme, millest viskepikkus sõltub: viskekiirusest p, jalgratta kiirusest r, viskenurgast θ ning gravitatsioonilisest g kiirendusest. Just nagu ootasime. Nüüd asume seda viskepikkust analüüsima!
Matemaatiline analüüs
Eesmärk on viskepikkust nurgast θ sõltuvalt maksimeerida. Võime esmalt vaadata, mis juhtub mingil konkreetsel juhul. Teame, et gravitatsiooniline kiirendus on
Eeldame näiteks, et veepommi viskekiirus on
ning rattasõidu kiirus näiteks
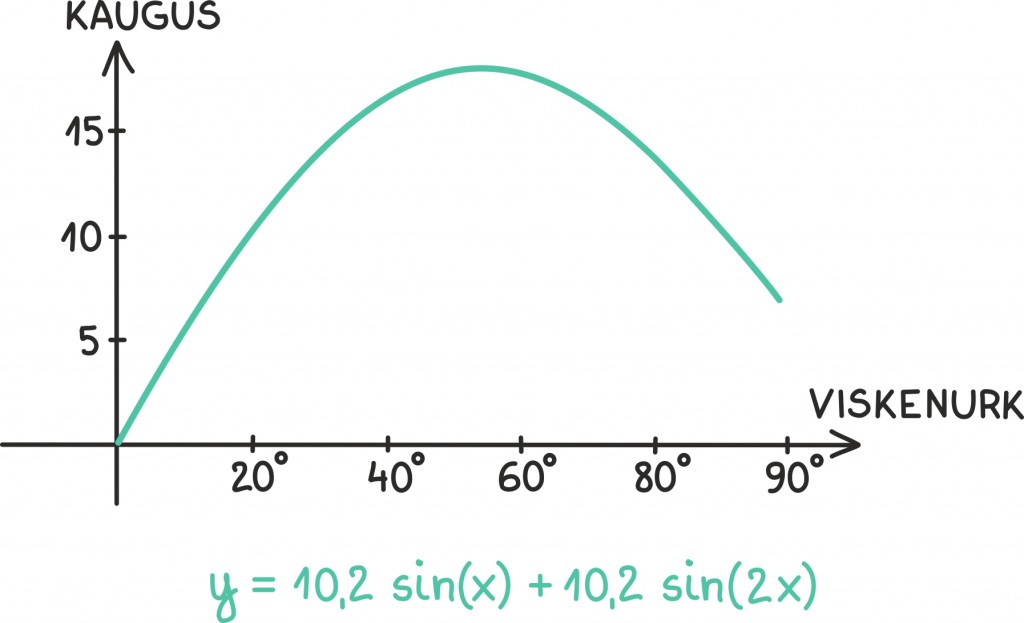
Sel juhul võime viskekauguse sõltuvust viskenurgast kirjeldada järgmisel graafikul:
Näeme, et veepomm lendab kõige kaugemale, kui viskenurk on veidi suurem kui 55º ja veidi väiksem kui 60º.
Kui tahame aga optimaalse viskenurga leida üldjuhul sõltuvuses viskekiirusest ning sõidukiirusest, peame lahendama ekstreemumülesande: maksimaalse kauguse korral on kauguse tuletis viskenurga suhtes võrdne nulliga. Tõepoolest, nagu nägime, on funktsiooni maksimumis ja miinimumis puutujasirge paralleelne x-teljega ja seega on tuletis null [lk 328].
Samas, sellest, et punktis on tuletis null, ei selgu küll kohe, et tegemist on maksimumiga, sama hästi võiks tegemist olla ka miinimumiga. Siiski, vaadeldes eelnevat joonist või usaldades füüsikalist intuitsiooni, võime selle mure kõrvale jätta – konkreetsel juhul annab ekstreemum meile just nimelt maksimumi.
Leiame siis selle tuletise. Teame, et siinusfunktsiooni tuletis on koosinusfunktsioon [lk 251] ning analoogiliselt saab näidata, et funktsiooni sin(2θ) tuletis on 2cos(2θ).
Seega saame:
Ekstreemumi ning sel juhul just nimelt maksimumi leidmiseks peame tuletise nulliks seadma ehk lahendama võrrandi:
Võime seda võrrandit lihtsustada, korrutades mõlemad pooled läbi liikmega
Nüüd on meil trigonomeetriline võrrand optimaalse viskenurga suhtes ning oleme juba heas seisus – parameetritena on mängus ainult viskekiirused ja viskenurk. Kas pole pisut huvitav, et gravitatsioonilise kiirenduse väärtus ei mängigi mingit rolli ehk et Kuu peal on optimaalne täpselt sama viskenurk, mis Maa peal!
Edasi peame veidi kavaldama, et leida lahend nurga θ suhtes.
Kasutame topeltnurga valemit [lk 245]
ja saame sarnaseid liikmeid koondades:
Nüüd jääb veel vaid lahendada ruutvõrrand cos(θ) suhtes, mille lahendame ruutvõrrandi lahendivalemi abil [lk 275]:
Mõistliku vastuse annab ilmselt ainult üks kahest lahendist. Näiteks võime eeldada, et vise ja liikumine on samas suunas ning et liikumine on positiivses suunas. Seega peaks viskenurk olema 0 ja 90 kraadi vahel. Kuna selles piirkonnas on koosinusfunktsioon positiivne, peame valima ka positiivse lahendi:
See ongi üldkujul lahend. Iga konkreetse juhu jaoks võiksime nüüd siia arvud sisse visata ning järeldusi teha.
Mida järeldada?
Järeldusi saame aga kaardistada ka üldisemalt.
Nimelt kuna teame, et 0 ja 90 kraadi vahel on koosinusfunktsioon rangelt kahanev, võime graafikult iga koosinusfunktsiooni väärtuse kohta leida ka nurgaväärtuse. Seost, mis selle annab, nimetatakse ka arkuskoosinuseks ning tähistatakse arccos θ. Nii võiks lahendi lausa välja kirjutada:
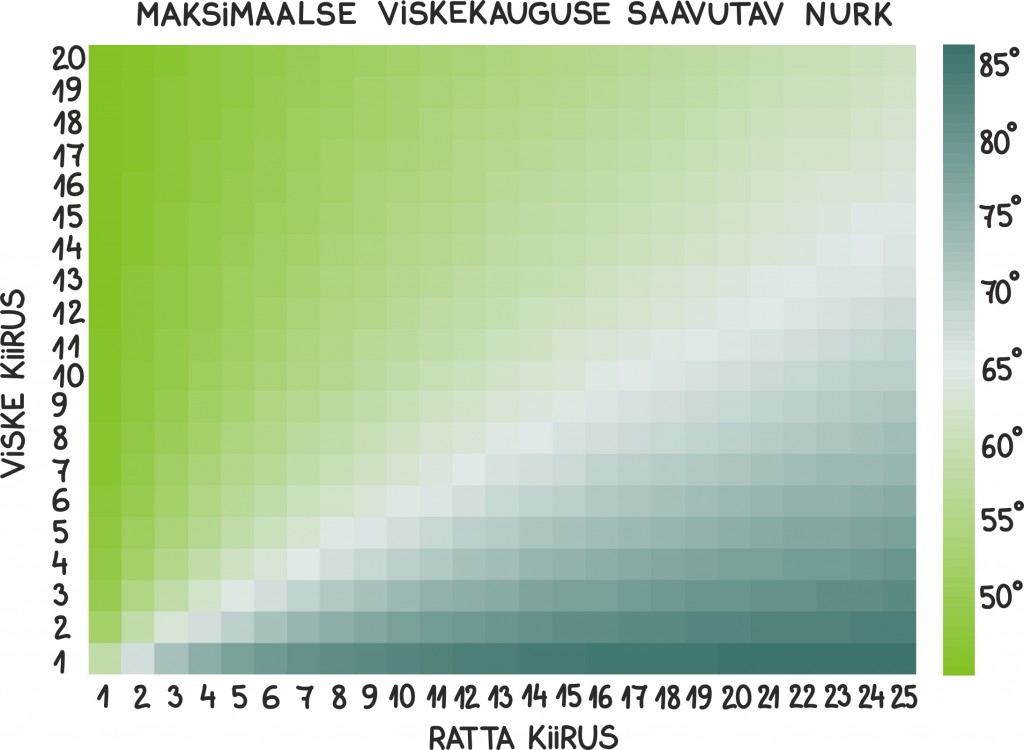
Nüüd võime selle lahendi abil koostada pildi, mis näitab, kuidas optimaalne viskenurk sõltub viskekiirusest ning liikumiskiirusest.
Nagu näeme, tuleb suurte kiiruste korral tõesti oma strateegiat muuta. Näiteks kui ratta kiirus on 20 m/s ja viske kiirus on 5 m/s, siis pikima viske saavutaks umbes 77° puhul, mis on juba päris erinev 45 kraadist. Samas väikeste kiiruste puhul suurt vahet pole.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!
