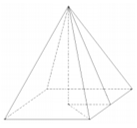
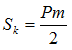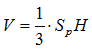KORRAPÄRASED PÜRAMIIDID
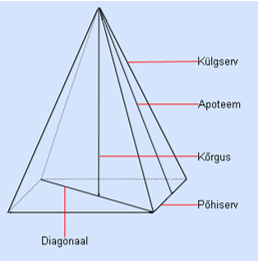
Püramiidiks nimetatakse hulktahukat, mille üks tahk on hulknurk ja kõik ülejäänud tahud on ühise tipuga kolmnurgad. Hulknurka nimetatakse püramiidi põhjaks ja ühise tipuga kolmnurki külgtahkudeks. Püramiidi põhja külgi nimetatakse püramiidi põhiservadeks ja külgtahkude ühiseid servi külgservadeks. Külgservade ühine punkt on püramiidi tipp. Tipu kaugus põhjast on püramiidi kõrgus h. Püramiidi külgtahu kõrgust nimetatakse apoteemiks m.
Püramiidi nimetatakse korrapäraseks siis, kui selle põhjaks on korrapärane hulknurk ja püramiidi kõrguse aluspunkt asub põhja keskpunktis. Korrapärase püramiidi kõik külgtahud on võrdsed võrdhaarsed kolmnurgad.
Sulle võivad huvi pakkuda need õppematerjalid:
Funktsioonide graafikute lõikepunktide leidmine
Algebralised murrud
Liitmine 20 piires
II kooliastme matemaatika reeglite kordamine
Liitmine ja lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruumilised kujundid
Kell ja kellaaeg
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine I kooliastmele
Hariliku murru kordamine
Funktsioonid ja nende graafikud
Ruutjuur, tehted ruutjuurtega
Funktsioonide graafikud
Kirjalik lahutamine
Lahutamine 20 piires
Tasandilised kujundid
Liitmine 10 piires
Ratsionaalavaldised
Harjutusülesandeid matemaatika riigieksamiks
Põhiservade arvu järgi jagatakse püramiidid kolmnurkseteks, nelinurkseteks, viisnurkseteks, ehk üldiselt n-nurkseteks.
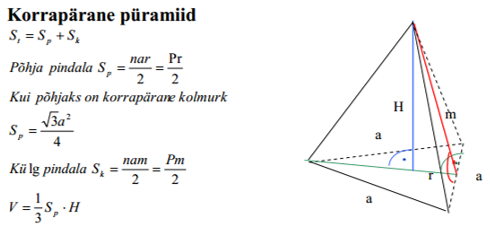
Püramiidi põhja pindala Sp on põhjaks oleva hulknurga pindala.
Korrapärase püramiidi külgpindala Sk on võrdne põhja ümbermõõdu ja apoteemi m poole korrutisega.
Püramiidi täispindala St võrdub põhja pindala ja külgpindala summaga.
Püramiidi ruumala V võrdub ühe kolmandikuga põhja pindala ja kõrguse korrutisest.
Korrapärane kolmnurkne püramiid
Korrapäraseks kolmnurkseks püramiidiks nimetatakse korrapärast püramiidi, mille põhjaks on võrdkülgne kolmnurk.
Püramiidi kõrgus jaotab kolmnurkse põhja kõrguse osadeks, kus ![]() põhja kõrgusest jääb kolmnurga tipu poolsesse osasse ja
põhja kõrgusest jääb kolmnurga tipu poolsesse osasse ja ![]() kolmnurga aluse poolsesse osasse.
kolmnurga aluse poolsesse osasse.
Korrapärane tetraeeder
Korrapärane tetraeeder ehk korrapärane nelitahukas ehk regulaarne nelitahukas on korrapärane hulktahukas, millel on neli võrdkülgse kolmnurga kujulist tahku ja mille igast tipust lähtub kolm serva.
Korrapärane nelinurkne püramiid
Korrapäraseks nelinurkseks püramiidiks nimetatakse korrapärast püramiidi, mille põhjaks on ruut.
Küsimused püramiidide kohta:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!