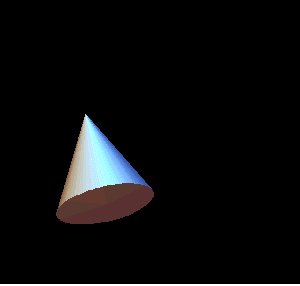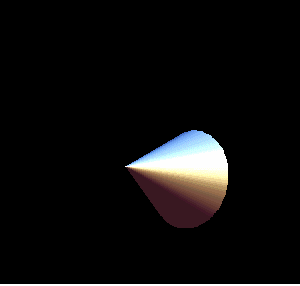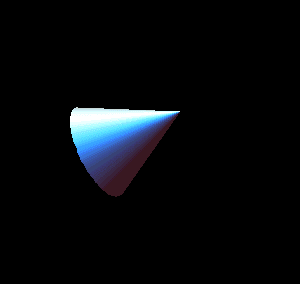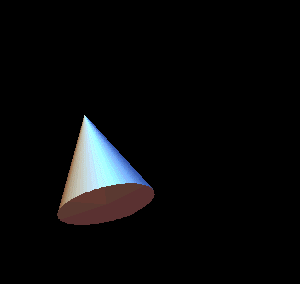KOONUS
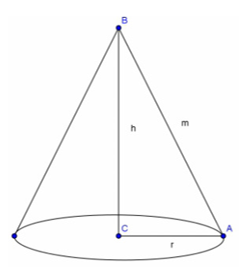
Koonus on keha, mille moodustab ühe oma kaateti ümber pöörlev täisnurkne kolmnurk.
Kaatet BC, mille ümber pöörleb koonust moodustav täisnurkne kolmnurk, on koonuse teljeks.
Kolmnurga hüpotenuus AB on koonuse moodustajaks. Koonuse moodustajat tähistatakse tavaliselt tähega m.
Pöörleva kolmnurga teine kaatet AC moodustab ringi, mida nimetatakse koonuse põhjaks. Lõiku AC, mis on koonuse põhja raadius, tähistatakse ka tähega r.
Kolmnurga hüpotenuus moodustab pöörlemisel koonuse külgpinna.
Punkti B nimetatakse koonuse tipuks ning tipu kaugust koonuse põhjast (lõiku BC) koonuse kõrguseks ning tähistatakse tavaliselt tähega h.
Sulle võivad huvi pakkuda need õppematerjalid:
Funktsioonide graafikute lõikepunktide leidmine
Algebralised murrud
Liitmine 20 piires
II kooliastme matemaatika reeglite kordamine
Liitmine ja lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Ruumilised kujundid
Kell ja kellaaeg
Ruutvõrrandi abil lahenduvad tekstülesanded
Peastarvutamine I kooliastmele
Hariliku murru kordamine
Funktsioonid ja nende graafikud
Ruutjuur, tehted ruutjuurtega
Funktsioonide graafikud
Kirjalik lahutamine
Lahutamine 20 piires
Tasandilised kujundid
Liitmine 10 piires
Ratsionaalavaldised
Harjutusülesandeid matemaatika riigieksamiks
Koonuse täispindala St on külgpindala Sk ja põhitahu pindala Sp summa:
\({S_{t}}={S_{k}}+{S_{p}}\)
Koonuse külgpindala võrdub põhja ümbermõõdu ja külgtahu kõrguse poole korrutisega:
\({S_{k}=\pi r m}\)
Koonuse ruumala on võrdne kolmandikuga selle põhja pindala Sp ja koonuse kõrguse H korrutisega:
Koonuse põhjaks on ring – järelikult põhja ümbermõõt ning põhja pindalad on ringi ümbermõõt ja pindala.
Koonus
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!