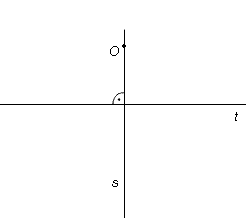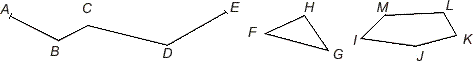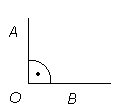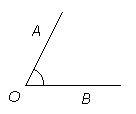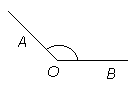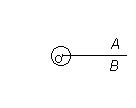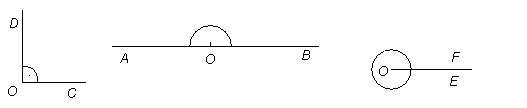Geomeetrilised kujundid
Geomeetrilised kujundid
Selleks, et tutvuda vastava kujundiga lähemalt, tee hiireklõps vastaval kujundil. (Paremini nähtav arvutis)
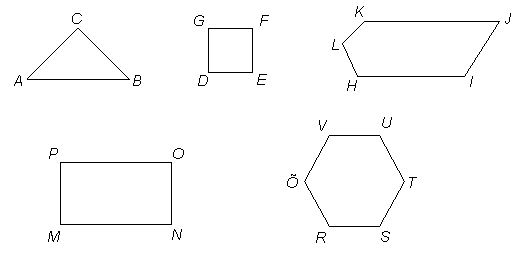
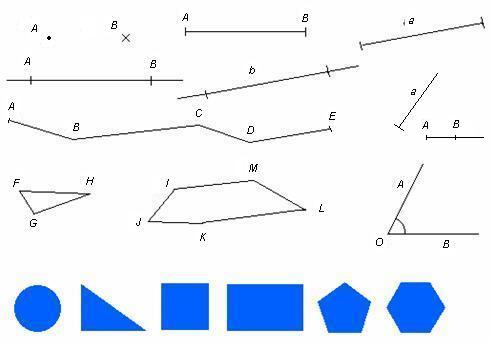
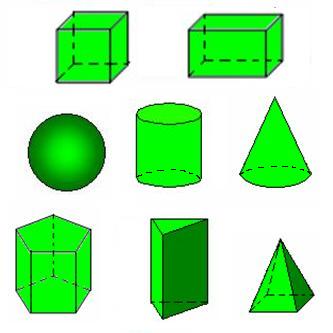
Tasapinnalisi geomeetrilisi kujundeid.
Ruumilisi geomeetrilisi kujundeid.
Sulle võivad huvi pakkuda need õppematerjalid:
Peastarvutamine I kooliastmele
Funktsioonide graafikud
Kirjalik liitmine
Lahutamine 20 piires
Funktsioonid ja nende graafikud
Ratsionaalavaldised
Algebralised murrud
Ruutjuur, tehted ruutjuurtega
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonide graafikute lõikepunktide leidmine
Liitmine 10 piires
Liitmine ja lahutamine 10 piires
Peastarvutamine eelkoolile
Üksliikmed, hulkliikmed ja tehted nendega
Liitmine 20 piires
Kell ja kellaaeg
Kirjalik lahutamine
Tasandilised kujundid
Harjutusülesandeid matemaatika riigieksamiks
II kooliastme matemaatika reeglite kordamine
Punkt
Punkt on kõige lihtsam geomeetriline kujund. Punktil ei ole mõõtmeid, st pikkust ega laiust.
Punkti tähistatakse joonisel tavaliselt punkti, risti või väikese ringiga.
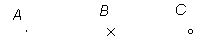
Ristiga punkti märkimisel loetakse punktiks joonte ristumise koht.
Punkt tähistatakse suure tähega, näiteks joonisel A, B ja C.
Neid punkte loetakse: punkt A, punkt B, punkt C.
Sirge
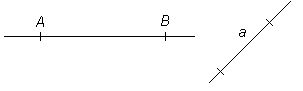
Sirglõigu pikendamisel üle mõlema otspunkti saame sirge. Sirge pikkust ei ole võimalik mõõta, sest sirglõiku võib pikendada üle mõlema otspunkti lõpmatult kaugele. Läbi kahe punkti saame joonestada ainult ühe sirge.
Joonisel olevaid sirgeid tähistame: sirge AB ning sirge a. Sirget ja lõiku eristame eelneva sõnaga, näiteks sirge AB ja lõik AB.
Ristsirge
Ristsirged ehk ristuvad sirged on kaks lõikuvat sirget, mis lõikumisel moodustavad täisnurga.
Joonestame antud sirgele ristsirge
- läbi antud punkti O, mis asetseb antud sirgel (Nähtav arvutis) t;
- läbi antud punkti O, mis asetseb väljaspool antud sirget (Nähtav arvutis) t.
Kahe sirge vastastikune asend tasandil
Kaks sirget tasandil on alati kas lõikuvad, paralleelsed või kattuvad.
Kaks sirget on lõikuvad, kui neil on ainult üks ühine punkt.
Kaks sirget on paralleelsed, kui neil pole ühtegi ühist punkti.
Kaks sirget on kattuvad, kui kõik nende punktid on ühised.
Sirglõik ehk lõik
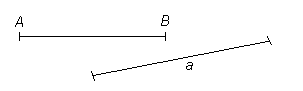
Kui kaks punkti ühendada sirge joonega, saame sirglõigu. Sirglõiku nimetatakse sageli ka lihtsalt lõiguks.
Sirglõiku tähistatakse kas otspunktide märkimisega AB või ühe tähega a.
Joonisel kujutatud sirglõike loetakse: „Lõik AB ja lõik a.”
Sirglõigu pikkust märgitakse järgmiselt: AB = 4 cm või a = 5 cm.
Kiir
Sirglõigu pikendamisel üle ühe otspunkti saame kiire. Kiire pikkust ei ole võimalik mõõta, sest sirglõiku saab pikendada üle ühe otspunkti lõpmatult kaugele.
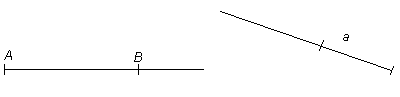
Sirglõikdiagramm
Sirglõikdiagrammis kasutatakse arvandmetest piltliku ettekujutuse saamiseks lõike.
Näide 1.
Näide 2.
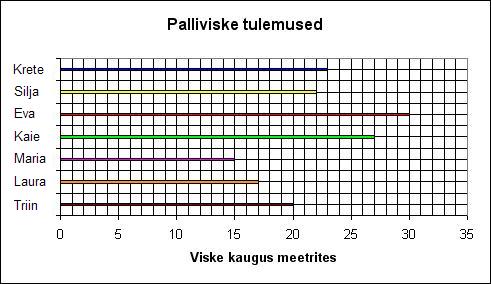
Kolmanda klassi õpilased heegeldasid tööõpetuse tunnis lõngast ketti. Tunni lõpul mõõdeti kettide pikkused. Koostame tulemuste põhjal sirglõikdiagrammi.
Sisesta heegeldatud kettide pikkused sentimeetrites.
Andmete sisestamiseks vajuta hiirega siia. (Nähtav arvutis)
Murdjoon
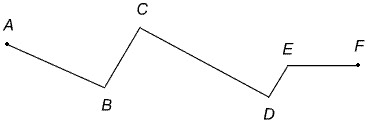
Murdjoon koosneb punkte järjestikku ühendavatest lõikudest, kusjuures kolm järjestikust punkti ei asu ühel sirgel.
Joonisel on murdjoon ABCDE.
Antud punkte ühendavad lõigud on murdjoone lülid.
Lõikude otspunktid on murdjoone tipud.
Iga murdjoon on pikem tema otspunkte ühendavast lõigust.
Kui murdjoone otspunktid ei ühti, on murdjoon lahtine (murdjoon ABCDE). Kui murdjoone otspunktid ühtivad, on see kinnine murdjoon (murdjoon FGH ja murdjoon IJKLM). Kinnine murdjoon moodustab hulknurga.
Murdjoone pikkus
Murdjoone pikkus on võrdne teda moodustavate sirglõikude pikkuste summaga.
Näide.
Olgu murdjoone lülide pikkused 3 cm, 2 cm, 4 cm, 1 cm ja 2 cm. Leiame murdjoone pikkuse.
3 + 2 + 4 + 1 + 2 = 12 (cm)
Vastus. Murdjoone pikkus on 12 cm. (Nähtav arvutis)
Hulknurk
Hulknurga moodustab tasandil olev kinnine murdjoon. Murdjooneks nimetatakse niisugust kujundit, mis koosneb punkte järjestikku ühendavatest lõikudest, kusjuures kolm järjestikust punkti ei asu ühel sirgel.
Hulknurka, millel on võrdsed küljed ja võrdsed nurgad, nimetatakse korrapäraseks hulknurgaks.
Kõikide hulknurkade (kolmnurk, nelinurk, ristkülik, ruut jt) korral mõeldakse nende kujundite all
1) kinnist murdjoont ja
2) kinnist murdjoont koos tasandi osaga, mida see murdjoon piirab.
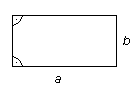
Ristkülik
Ristkülik on nelinurk, mille kõik nurgad on täisnurgad.
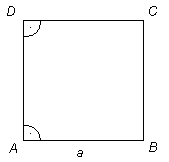
Ruut
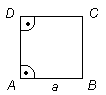
Ruuduks nimetatakse võrdsete külgedega ristkülikut.
Ruut on kinnine murdjoon, mis koosneb neljast ühepikkusest lülist.
Ruudul on neli tippu.
Ruudu kõik küljed on võrdse pikkusega.
Ruudu kõik nurgad on täisnurgad, s.o 90o.
Ruudu pindala
Pindala suurus näitab, mitu ühikruutu katavad kujundi.
S = a2
S – ruudu pindala
a – ruudu külje pikkus
pindala = külje pikkus · külje pikkus
Näide.
Leiame ruudu pindala, kui ruudu külje pikkus a = 6 cm.
S = 62 = 6 · 6 = 36 (cm2)
Vastus. Ruudu pindala on 36 cm2.
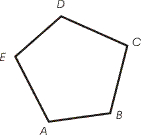
Viisnurk
Viisnurga moodustab viiest lülist koosnev kinnine murdjoon koos sellega piiratud tasandi osaga.
Joonisel on viisnurk ABCDE.
Viisnurgal on 5 külge, 5 tippu ja 5 nurka. Viisnurga nurkade summa on 540º.
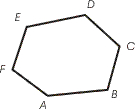
Kuusnurk
Kuusnurga moodustab kuuest lülist koosnev kinnine murdjoon koos selle poolt piiratud tasandi osaga.
Joonisel on kuusnurk ABCDEF.
Kuusnurgal on 6 külge ja 6 tippu.
Kuusnurga nurkade summa on 720o.
Nurk
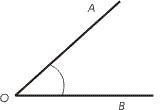
Nurga moodustavad kaks ühest ja samast punktist väljuvat kiirt koos tasandi osaga, mis jääb nende kiirte vahele.
Joonisel on kujutatud nurk AOB. Kiirte alguspunkt O on nurga tipp. Kiiri OA ja OB nimetatakse haaradeks. Punkt O on nurga tipp, tipust väljuvad haarad OA ja OB. Vaadeldavat nurka märgitakse kaarega nurga sees.
Nurka märgitakse lühidalt  AOB või lihtsalt
AOB või lihtsalt  O. Täht, mis tähistab nurga tippu, kirjutatakse nurga keskele.
O. Täht, mis tähistab nurga tippu, kirjutatakse nurga keskele.
Nurga tähistamiseks kasutatakse vahel ka kreeka tähestiku väiketähti 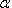 alfa,
alfa, 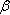 beeta ja
beeta ja 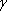 gamma.
gamma.
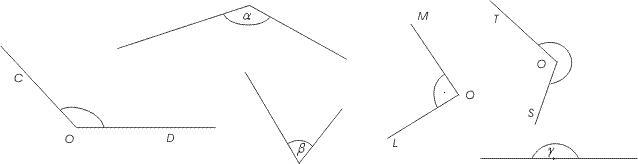
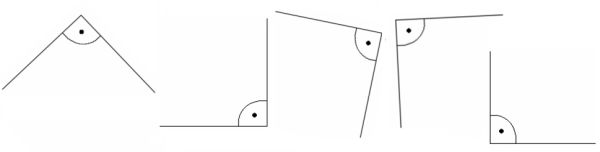
Näiteid nurkadest:
Nurkade liigitamine
Täisnurk
Täisnurk on nurk, mille suurus on 90o.
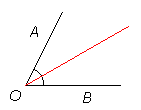
Nurgapoolitaja
Nurgapoolitaja on kiir, mis lähtub nurga tipust ja poolitab antud nurga.
Nurgapoolitaja iga punkt on nurga mõlemast haarast ühel ja samal kaugusel.
Kuidas joonestada nurgapoolitajat? (Nähtav arvutis)
Nurkade võrdlemine
Kahe nurga võrdlemiseks tuleb üks nurk paigutada teise peale nii, et nende tipud ja ühed haarad ühtivad. Seejärel tuleb vaadata, kuhu langeb pealmise nurga teine haar. Vastavalt sellele saab määrata, kumb nurkadest on suurem, kumb väiksem või on nad võrdsed. Nurga suurus ei olene nurga haarade pikkusest.
Nurkade võrdlemisel võib esineda kolm võimalust.
- Teine haar langeb nurga sisse.Näide.Võrdleme nurki AOB ja CDE. Vaata nurkade võrdlemist. (Nähtav arvutis)
 AOB >
AOB >  CDE
CDE
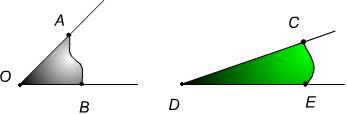
- Teine haar langeb väljapoole nurka. Näide.Võrdleme nurki AOB ja EFG. Vaata nurkade võrdlemist. (Nähtav arvutis)
 AOB <
AOB <  EFG
EFG
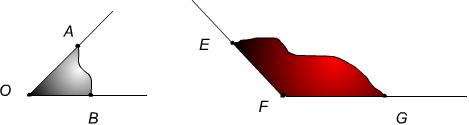
- Teine haar langeb alumise nurga teise haara peale.Näide.Võrdleme nurki AOB ja LMN. Vaata nurkade võrdlemist. (Nähtav arvutis)
 AOB =
AOB =  LMN
LMN
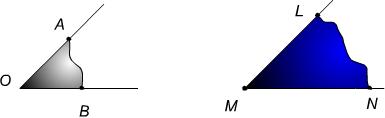
Kõrvunurgad
Kõrvunurkadeks nimetatakse kaht nurka, millel üks haar on ühine ja mille teised haarad moodustavad sirge.
Kõrvunurkade summa on 180o (sirgnurk). Kui on antud üks kahest kõrvunurgast, saame arvutada teise, lahutades 180o-st teadaoleva nurga suuruse.
Näide.
Nurga 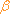 suurus on 45o. Leiame, kui suur on nurk
suurus on 45o. Leiame, kui suur on nurk  .
.
180o – 45o = 135o
Vastus. Nurk  on 135o.
on 135o.
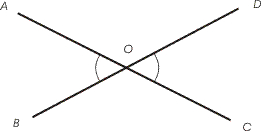
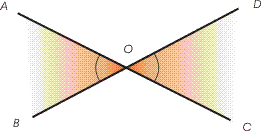
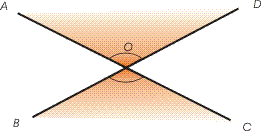
Tippnurgad
Kaht nurka nimetatakse tippnurkadeks, kui ühe nurga haarad on teise nurga haarade pikendused üle nende ühise tipu.
Tippnurgad on võrdsed.
Joonisel on tippnurgad AOB ja COD
Samuti on tippnurgad AOD ja BOC
Nurga mõõtmine
Nurga suuruse mõõtmiseks kasutatakse malli. Mall paigutatakse nurgale nii, et nurga tipp asetseks malli keskpunktis ja mõõdetava nurga üks haar läbib malli nullpunkti. Mallil on tavaliselt kaks skaalat, neist ühe nullpunkt on vasakul, teise nullpunkt paremal pool. Kriipsuke skaalal, mida läbib teine haar näitab nurga suurust kraadides.
Kuidas lugeda tulemust, kas välimiselt skaalalt või sisemiselt skaalalt? Tulemust loeme sellelt skaalalt, mille nullpunkti läbib nurga üks haar.
Näide 1. (Nähtav arvutis)
Näide 2. (Nähtav arvutis)
Nurgakraad
Nurga suurust mõõdetakse kraadides. Nurk suurusega 1 kraad saadakse, kui täisnurk jaotatakse 90 võrdseks osaks. Nurga kraadi tähistatakse 1°.
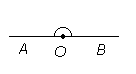
Täisnurga suurus on 90°, sirgnurga suurus on 180°, täispööre on 360°.
Peegeldustelg
Joonisel on kolmnurk A’B’C’ saadud kolmnurga ABC peegeldamisel sirgest t. Sirge t on peegeldustelg. Kolmnurgad ABC ja A’B’C’ on võrdsed, sest neid saab paigutada teineteisele nii, et nad ühtivad. (Nähtav arvutis)
![]() ABC =
ABC = ![]() A’B’C’
A’B’C’
Kolmnurk A’B’C’ on kolmnurga ABC kujutis.
Kolmnurkade punktid A ja A’, B ja B’, C ja C’ on sümmeetrilised sümmeetriatelje t suhtes. Need kolmnurgad on sirge t suhtes sümmeetrilised.
- Sümmeetrilised punktid asuvad sümmeetriateljega risti olevatel lõikudel.
- Sümmeetrilised punktid asuvad sümmeetriateljest võrdsetel kaugustel.
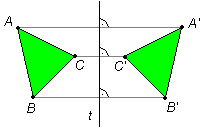
Kuidas joonestada sirge suhtes antud punktiga sümmeetriline punkt? (Nähtav arvutis)
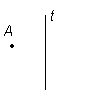
Kuidas peegeldada kolmnurk ABC sirgest t? (Nähtav arvutis)
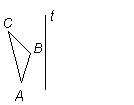
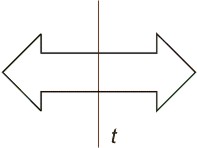
Sümmeetriatelg
Sümmeetriatelje suhtes on kujundi mõlemad pooled peegelpildilised.
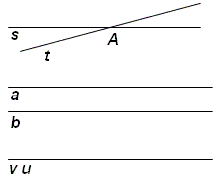
Sirge t on joonisel sümmeetriatelg.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!