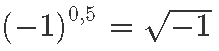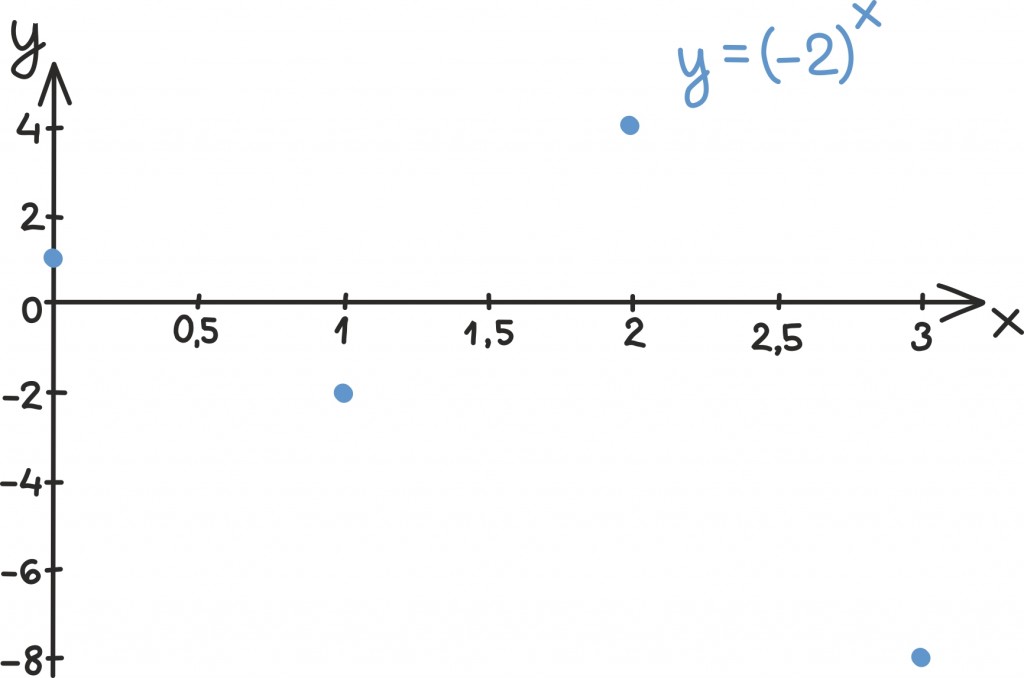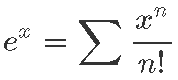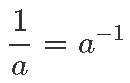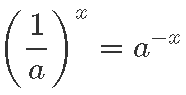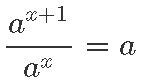Eksponentsiaalfunktsioon
Kui mõni pahaloomuline bakter on organismi jõudnud, ei pruugi sellest algul aimugi saada, sest iga bakteripere ei hakka kohe tramburaid korraldama, vaid ootab vahel veel päris mitmeid tunde. Miks nii?
Nimelt ei ole ühel või kahel või isegi tuhandel bakteril mõtet hakata vallatusi tegema ja mürkaineid eritama, sest immuunsüsteem saadaks selle peale kohe välja oma ustava armee ja teeks neile tuule alla.
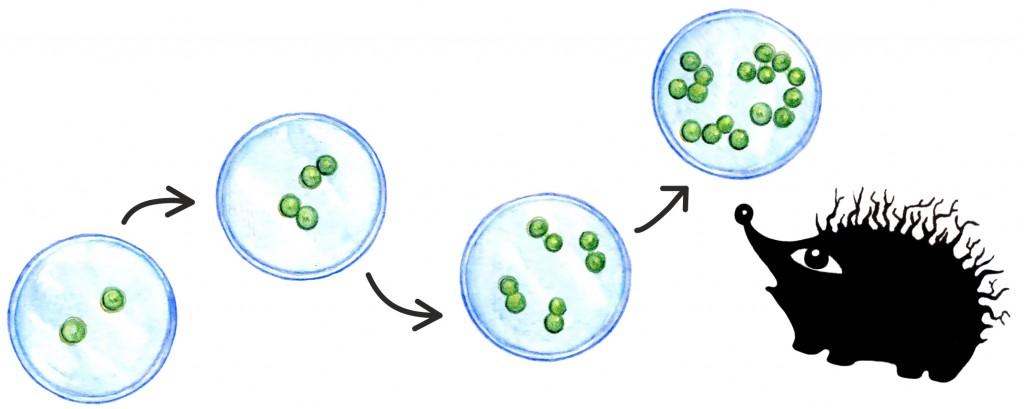
Seega paljunevad bakterid vaikselt, kuni neid on piisavalt palju, ja hakkavad alles seejärel kurja tegema. Sel juhul on immuunsüsteem juba raskustes. Bakteritel ei lähe paljunemiseks eriti palju aega, sest iga bakter pooldub ideaalsetes tingimustes umbes iga poole tunni järel.
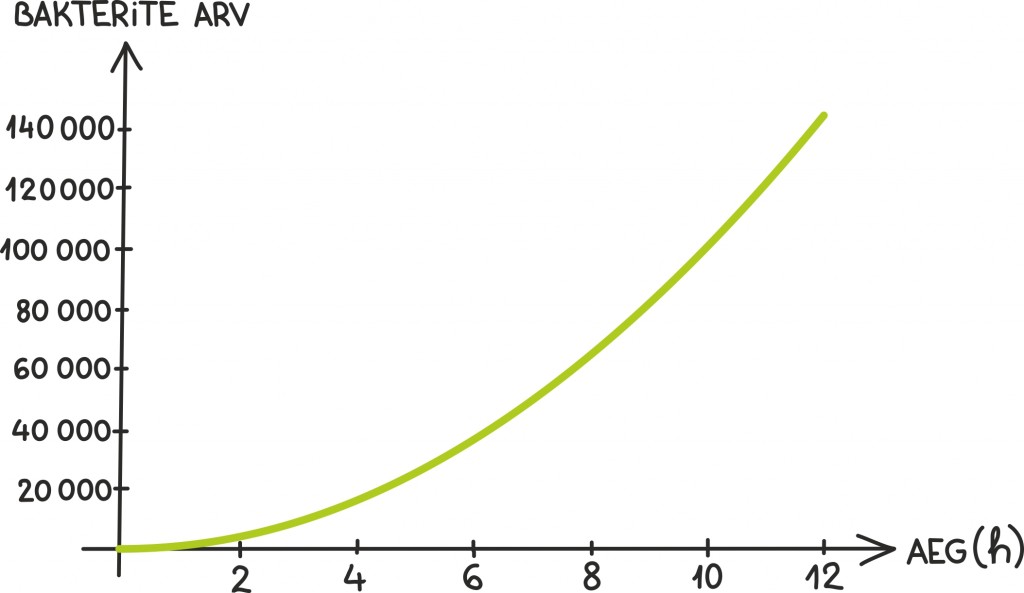
Selle tagajärjeks on väga kiire kasv! Näiteks kui 1000 bakteril lasta ideaalsetes tingimustes seltsida, kasvab nende arv järgmise 12 tunni jooksul järgnevalt:
Juba poole päevaga on tuhandest saanud rohkem kui sada tuhat! Tuleb välja, et saadud graafikut kirjeldab täpselt üks ilus ja tähtis funktsioon: eksponentsiaalfunktsioon. Ja kuigi maos ei ole bakteritele ideaalsed kasvutingimused, aitab see ikkagi ehk piisavalt hirmutada – ka pisike pahaloomuline bakteripere on juba ohtlik!
Eksponentsiaalfunktsioon ja astendamine
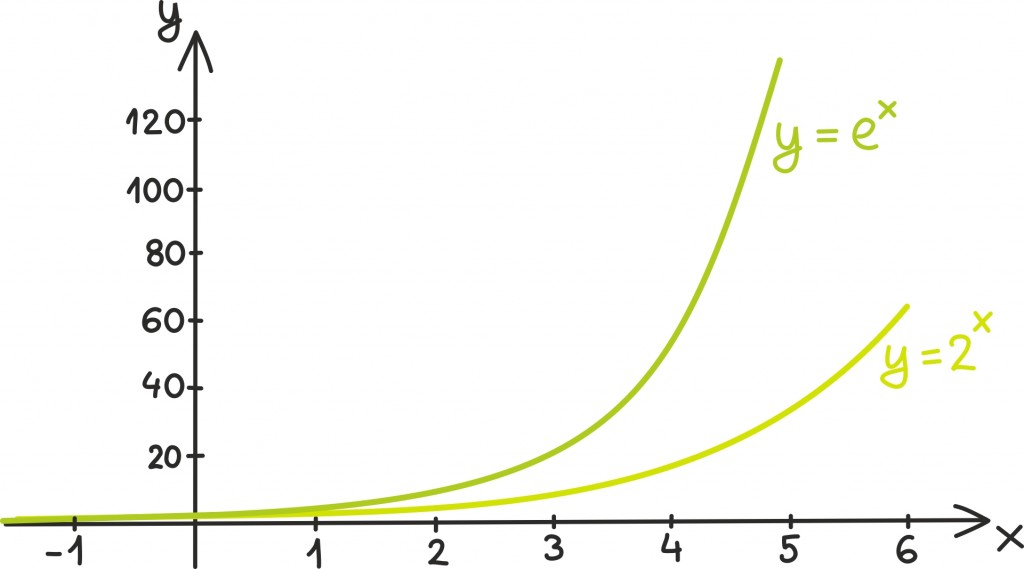
Eksponentsiaalfunktsioonideks on näiteks funktsioonid y = 2x või y = ex, kus x võib olla ükskõik mis reaalarv.
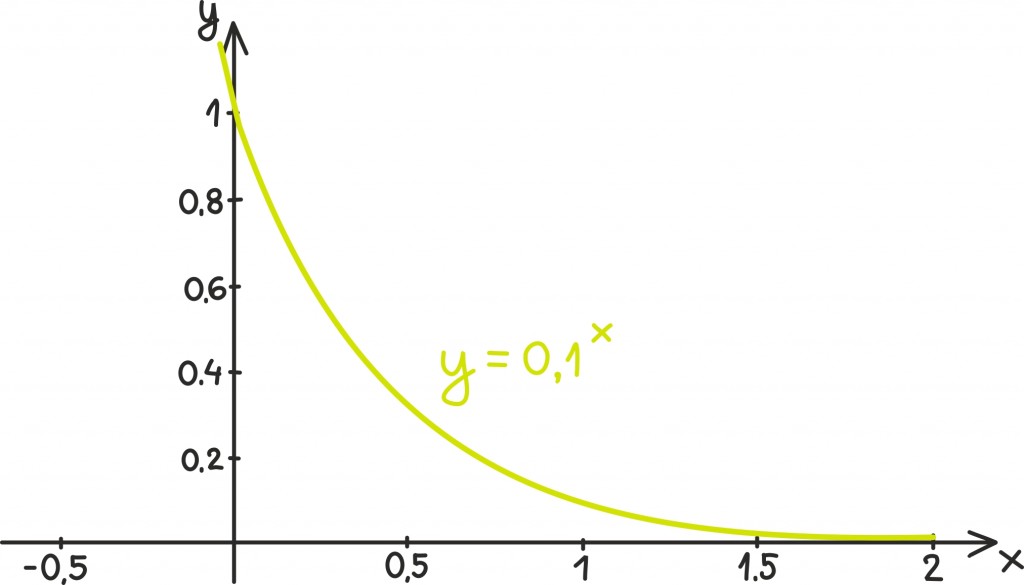
Samuti võib eksponentsiaalfunktsiooni alus olla ühest väiksem, näiteks y = 0,1x.
Üldkujul on eksponentsiaalfunktsioon kujus ax, kus aon positiivne reaalarv. Õpikutes otsustatakse tihti ka lisada tingimus, et a ≠ 1. Seda lihtsalt selle jaoks, et välistada konstantne funktsioon y = 1. Mõnikord arvatakse juurde veel ka kordaja: loetakse eksponentsiaalfunktsiooniks ka funktsioone b · ax, kus b on suvaline reaalarv.
Seda, miks a peab olema positiivne, selgitab kõige paremini üks võimalik eksponentsiaalfunktsiooni definitsioon: eksponentsiaalfunktsiooni näol ei ole tegemist millegi enama kui astendamise laiendamisega irratsionaalarvulistele astmetele ja astme aluselt nõudsime ju ka positiivsust [lk 110].
See laiendus on täpselt analoogne ratsionaalarvude reaalarvudele laiendamisega: tuleb lihtsalt graafikule jäävad imepisikesed augud täis toppida. Rangelt tähendab see ratsionaalarvulistele astmetele nende piirväärtuste lisamist [lk 313]. Negatiivsete aluste korral on graafik aga hüplik ja mingist aukude täitmisest seal väga juttu olla ei saagi.
Õigupoolest, nagu astme peatükist mäletame, tekib negatiivsete aluste korral häda juba täisarvulistelt astmetelt ratsionaalarvulistele üle minnes – et anda tähendus arvule
pidime ju sisse tooma hoopis kompleksarvud [lk 89]. Ühesõnaga negatiivsed alused jätame mängust välja.
Eksponentsiaalfunktsiooni võib defineerida ka teisiti. Näiteks alusel e võib eksponentsiaalfunktsiooni defineerida järgmise polünoomi meenutava avaldise abil:
Selle valemi tagamaid selgitasime natuke ilusate arvude peatükis [lk 106].
Sulle võivad huvi pakkuda need õppematerjalid:
Peastarvutamine I kooliastmele
Harjutusülesandeid matemaatika riigieksamiks
Ruutjuur, tehted ruutjuurtega
Lahutamine 20 piires
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Kell ja kellaaeg
Tasandilised kujundid
Ratsionaalavaldised
Geomeetria
Liitmine ja lahutamine 20 piires
Funktsioonide graafikute lõikepunktide leidmine
Liitmine 10 piires
Ruutvõrrand
Kirjalik liitmine
Üksliikmed, hulkliikmed ja tehted nendega
Kirjalik lahutamine
Ruutvõrrandi abil lahenduvad tekstülesanded
Väike protsendiamps
II kooliastme matemaatika reeglite kordamine
xy-koordinaatsüsteem
Eksponentsiaalfunktsiooni omadused
Eksponentsiaalfunktsioon ax on määratud kõikide reaalarvude korral ehk tema määramispiirkonnaks on reaalarvude hulk. Tema graafik on ilus ja pidev ehk teda võib joonistada pliiatsit paberilt tõstmata.
Eksponentsiaalfunktsiooni kuju sõltub tema alusest.
- Kui alus a on suurem kui üks, on ax kasvav funktsioon.
- Kui alus a asub nulli ja ühe vahel, siis on tegemist kahaneva funktsiooniga.
- Alusel üks on tegemist konstantse funktsiooniga, mida nii mõnigi kord eksponentsiaalfunktsioonide hulka ei loeta, kuna ta ei kasva ega kahane.
- Viimaks, nagu mainisime, negatiivsete aluste korral eksponentsiaalfunktsiooni defineerida ei saagi.
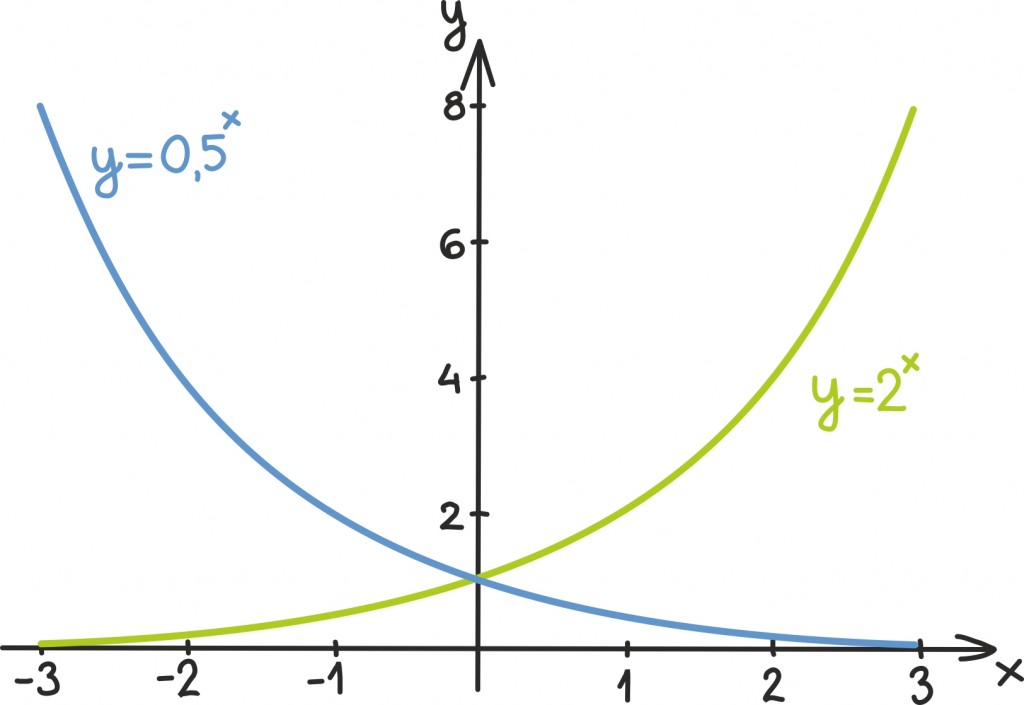
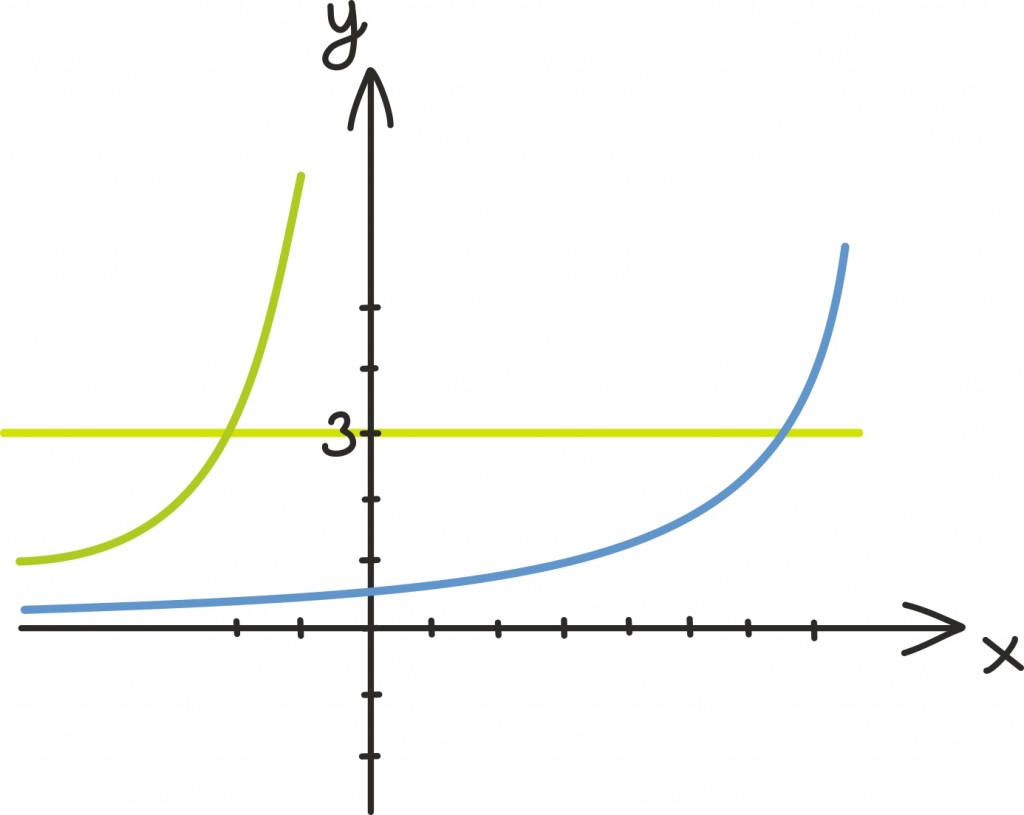
Selgub, et see, kas alus on ühest suurem või väiksem, ei muuda teatud mõttes eksponentsiaalfunktsiooni olemust, vaid lihtsalt tema suunda.
Nimelt on pöördarvulistel alustel (näiteks alustel 2 ja ½) eksponentsiaalfunktsioonid teineteise peegeldused y-telje suhtes. Ühel juhul rändab eksponentsiaalfunktsioon x-telje kohal nullist lõpmatusse ja teisel juhul vastupidi.
Miks see nii peaks olema, pole just raske näha: teame ju, et
ja seega
ax loetuna negatiivses suunas.
Eksponentsiaalfunktsiooni ax muutumispiirkonna moodustavad kõik positiivsed reaalarvud. Teisisõnu leidub iga positiivse reaalarvu b jaoks x, nii et ax = b. Selles võib ilmselt veenduda puhtalt graafikut vaadates – graafik on pidev, ühel pool läheneb nullile, teisel pool tormab lõpmatusse. Tegemist on olulise omadusega, mis võimaldab meil hiljem defineerida eksponentsiaalfunktsiooni pöördfunktsiooni – logaritmfunktsiooni [lk 290].
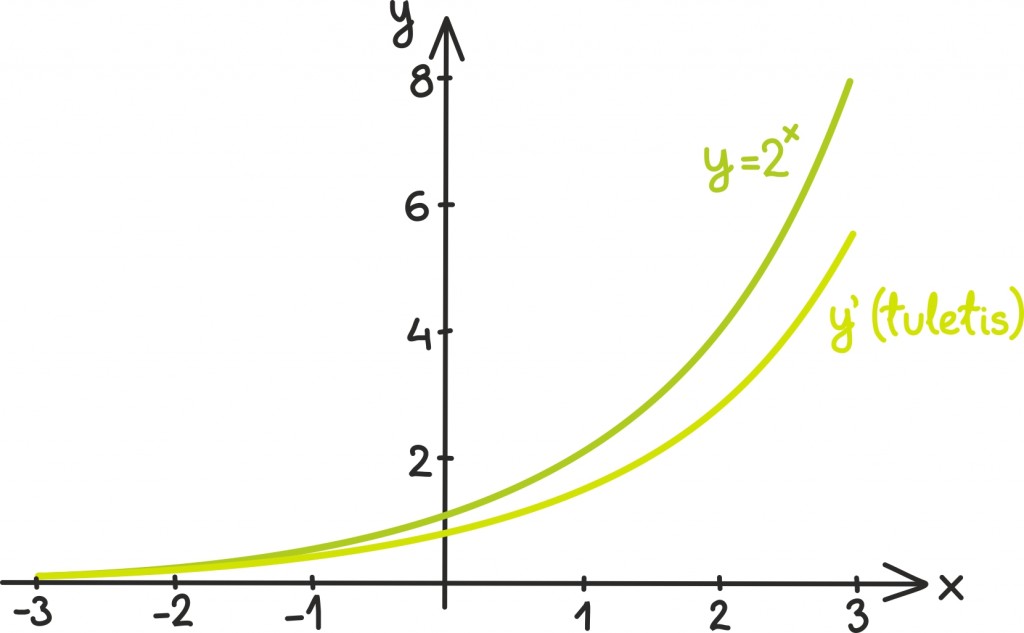
Eksponentsiaalfunktsiooni graafikut uurides näeme, et ühest suurema aluse korral kasvab ta aina kiiremini. Selgub, et asi on veelgi hullem – ka eksponentsiaalfunktsiooni kasvamise kiirus ehk tuletis [lk 320] kasvab järjest kiiremini, ja ka tema kiirendus ja nii edasi.
Funktsiooni kasvamise kiirust näitab tema tuletis. Selgub, et eksponentsiaalfunktsiooni ax tuletise võtmiseks tuleb funktsiooni ainult mingi reaalarvulise konstandiga läbi korrutada: ehk siis ax tuletiseks on b · ax, kus konstandi b väärtus sõltub a väärtusest. Seda fakti võib tõlgendada järgmiselt: eksponentsiaalfunktsiooni hetkeline kasv on alati võrdeline funktsiooni väärtuse endaga. See osutub oluliseks just kasvuprotsesside tõlgendamisel.
Eksponentsiaalfunktsioon kasvab igas kindlas vahemikus sama arv kordi. Tõepoolest, näiteks vahemikus pikkusega üks kehtib
iga reaalarvu x jaoks.
Üldisemalt võibki mõelda, et eksponentsiaalfunktsioon teeb liitmisest korrutamise. See on tegelikult juba astendamisest tuntud omadus:ax+y = ax · ay. Ka selle omaduse kaudu saab tegelikult eksponentsiaalfunktsiooni defineerida: tegemist ongi ainsa pideva reaalarvulise funktsiooniga, mis teeb liitmisest korrutamise ehk mille korral kehtib võrrand ƒ(x + y) = ƒ(x) · ƒ(y).
Eksponentsiaalfunktsioon erinevatel alustel
Nägime juba, et eksponentsiaalfunktsiooni axkäitumine sõltub tema alusest a. Huvitaval kombel võime aga tegelikult kõiki eksponentsiaalfunktsioone kirjutada ka ühel ja samal alusel – peame selle jaoks lihtsalt astendajat muutma.
Näiteks funktsiooni 4x võime kirjutada alusel 2 funktsioonina 22x ning alusel 16 funktsioonina 160,5x, sest ühtepidi 4 = 22 ja teisalt 4 = √16 = 160,5. Üldisemalt, kui tahame kirjeldada funktsiooni axalusel b, peame lihtsalt otsima välja arvu c nii et bc =a. See on iga positiivse reaalarvu a korral ka võimalik, kuna eksponentsiaalfunktsiooni muutumispiirkonnaks on kõik positiivsed reaalarvud.
Seega võime kirjutada
Funktsioonide ühel astmel kirjutamine on lihtsustav, sest nii on neid kergem omavahel võrrelda – näiteks oleks ju päris raske öelda, kas kiiremini kasvab protsess 50,5x või 30,8x. Jääb küsimus, milline ühine alus valida.
Mõnikord kasutatakse kümnendsüsteemist pärit alust 10, mis räägib kümnekordistamisest, mõnikord alust 2, mis räägib kahekordistamisest. Kõige enam kirjutatakse aga eksponentsiaalfunktsioon ilusa-arvulisele alusele e [lk 102]. Funktsioon ex annab teatud mõttes kõige loomulikuma kasvuprotsessi: sellel juhul on kasvu hetkekiirus alati täpselt võrdne hetkesuurusega ehk funktsioonide keeles: ex tuletis on igas punktis täpselt ex [lk 320].
Kasvavad ja kahanevad protsessid
Eksponentsiaalfunktsioonist on kõige õigem mõelda kui teatavat tüüpi väga kiirest kasvamisest või kahanemisest ajas. Nagu nägime, on eksponentsiaalse kasvamise korral kasvamise kiirus igal hetkel proportsionaalne ehk võrdeline koguse või suuruse endaga. Nii nimetatakse eksponentsiaalset kasvamist ka proportsionaalseks kasvamiseks. Just seetõttu kirjeldas ta ka bakterite koloonia laienemist – koloonia kasvu kiirus igal hetkel sõltub ju täpselt sellest, palju baktereid parasjagu pooldumas on, ehk tegelikult koloonia enda suurusest.
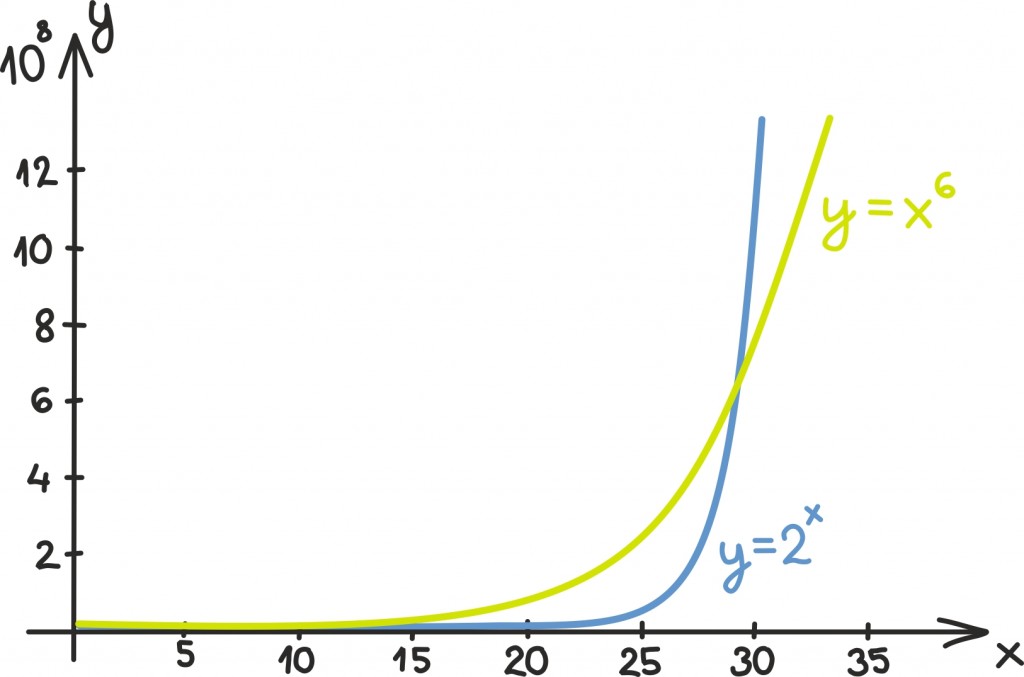
Eksponentsiaalne kasvamine on palju kiirem kui polünomiaalne ehk polünoomiga antud kasvamine.
Arvutite kiiruse kasv on eksponentsiaalne
Transistor on hirmutav sõna ja tõepoolest, selle taga peidab end võimas seade. Transistoreid kasutatakse elektrisignaalide tekitamiseks, võimendamiseks, muundamiseks ja lülitamiseks. Transistoritel põhineb kogu elektroonika ning nad on ka arvutite protsessorite arvutuskomponentideks.
Transistorite arv arvutis väljendab tema kiirust – seda, kui palju operatsioone ta suudab ajahetkes teha. Arvutite võimsus kasvab kiiresti, umbes iga kahe aasta järel kahekordistub transistorite arv protsessoris.
Teisisõnu umbes iga kahe aasta järel saab arvuti kaks korda võimsamaks:
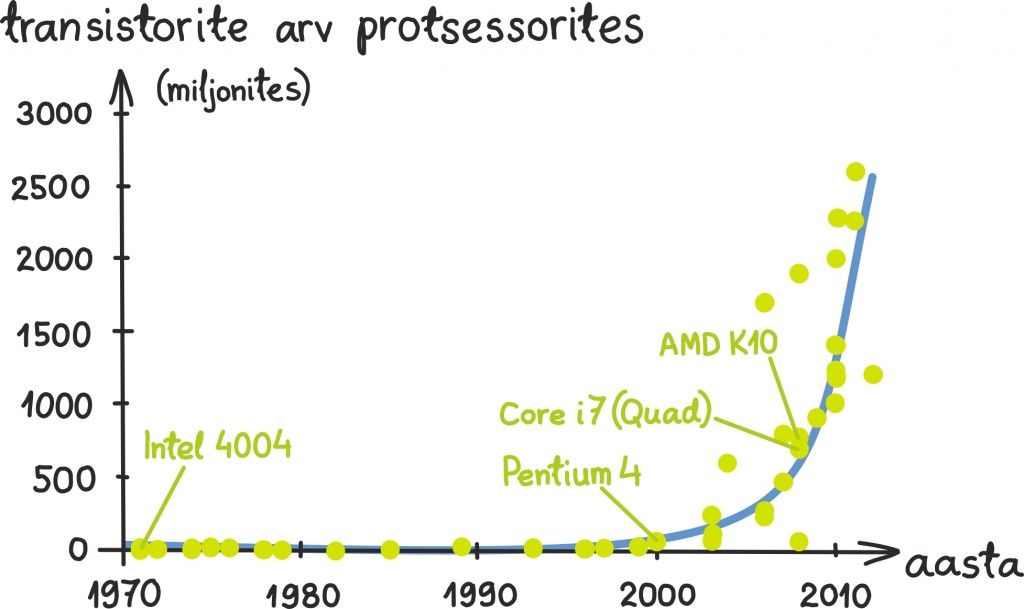
Seda seaduspära märkas esimest korda juba 1965. aastal arvutiprotsessorite tootja Inteli kaasasutaja Gordon E. Moore. Nii kutsutakse seaduspära vahel ka Moore’i seaduseks. Kasvu kiiruse illustreerimiseks kasutas Moore ise järgnevat analoogiat: kui autotööstus areneks sama kiiresti kui elektroonikatööstus, siis tänaseks sõidaks auto liitri bensiiniga miljon kilomeetrit ning odavam oleks auto maha kanda kui teda kesklinnas tunniks ajakski parkida.
Graafikut on natukene keeruline lugeda, sest esimesed punktid tunduvad kõik olevat praktiliselt nullis. See tuleneb just nimelt väga kiirest, eksponentsiaalsest kasvust. Tuleb välja, et sellisel juhul on mõttekas y-telge kujutada nii-öelda logaritmiliselt, kus ühikud ei muutu liitmise vaid korrutamise teel. Selle võtte kasulikkust näitame järgmises peatükis [lk 299].
Mõni arvutiprogramm jääb aga ikka aeglaseks
Kuna arvuti kiirus kahekordistub iga kahe aastaga, võiks arvata, et ükskõik kui keerulist tööd me ka arvutile ei annaks, varem või hiljem on see vaid minutite küsimus.
Siiski nii lihtne olukord ei ole. Nimelt on paljud ülesanded, mida arvutiga lahendada võiks, lahendatavad ainult eksponentsiaalse ajaga: see tähendab, et iga kord kui arvutiprogrammi sisendit suurendada ühe ühiku võrra, kasvab programmi aeg kindla arvu kordi. Näiteks võiks programmi aeg iga sisendi jaoks pikeneda kaks korda – sel juhul kirjeldaks aja kulumist funktsioon 2sisendi pikkusning isegi kui sisend pikkusega 10 võtaks 10 sekundit arvutusaega, siis sisend pikkusega 40 võtaks juba 340 aastat. Eluliste probleemide lahendamiseks on vahel aga vaja sisendeid suurusjärgus tuhat või isegi miljon.
Kuigi Moore’i seadus protsessorite kiirenemisest on üsna hämmastav, siis praeguse murega ta toime ei tule. Nimelt, oletame, et arvutustele kuluva aja kulumist kirjeldab tõesti eksponentsiaalfunktsioon 2sisendi pikkus. Sel juhul, isegi kui kaks korda rohkem transistoreid tähendaks tõesti ka kaks korda rohkem arvutusi ajaühikus, saaksime ühel arvutil arvutades iga kahe aasta järel sisendit vaid ühe ühiku võrra pikendada!
Sellest lähtuvalt ei või endiselt arvutiprogrammidega hooletu olla – tuleb leida häid ja efektiivseid viise arvutite tegemiseks ning selliste heade programmide kirjutamine on üks tänapäevase arvutiteaduse põhilisi eesmärke.
Temperatuuri ühtlustumine
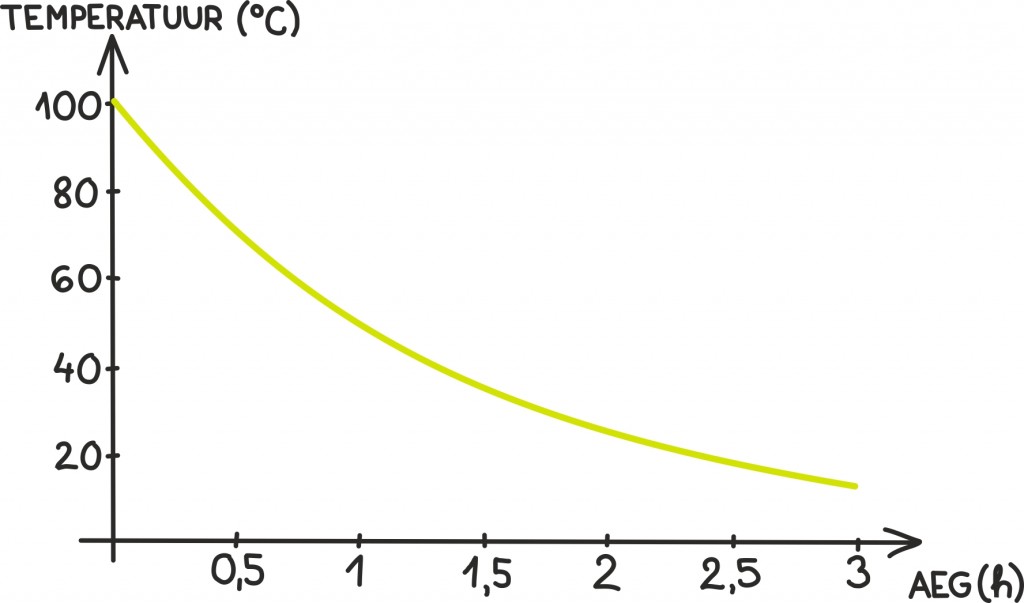
Oled äsja valanud endale tassi kohvi ja kohe jooma hakates põletaksid kindlasti oma keelt ja huuli. Õnneks pole sellest hullu. Selgub, et kohvi jahtumine toimub eksponentsiaalse kiirusega ehk nagu juba nägime – väga kiiresti.
Nimelt märkas juba Newton oma vaatlustest, et kui asetada üks väiksem keha suurde väliskeskkonda, siis sõltub selle väiksema keha temperatuuri muutumise kiirus proportsionaalselt väliskeskkonna ja keha temperatuuride erinevusest. Nagu juba teame, tähendab see aga täpselt, et temperatuuri ühtlustumine on antud eksponentsiaalse funktsiooniga. Seega kui väiksem objekt on alguses väliskeskkonnast soojem, kirjeldab temperatuuride vahe vähenemist hästi eksponentsiaalselt kahanev protsess kujus
kus t tähistab aega ning ΔT0 on lihtsalt algne vahe temperatuurides.
Kui tahate täpselt ennustama hakata, kui kiiresti kohv ikkagi jahtub, oleks esmalt vaja teha mõned katsed, mille abil määrate konstandi a, mis sõltub kohvi enda omadustest ja näiteks ka tassist.
Edaspidi on – vähemalt sama kohvi ning sama tassi korral – igal hommikul vaja ainult mõõta kohvi ja toa temperatuuri. Seejärel saad täpselt ennustada, kaua aega läheb, kuni kohv joodavaks muutub. Loomulik on küsida: mil määral need ennustused kehtivad ja mil määral nad erinevad rohelise tee, kuumade pirukate ja teistsuguste, näiteks suuremate ja väiksemate tasside jaoks? Aus vastus on, et ega me täpselt ei tea – rohelise tee jaoks ei tohiks suurt midagi muutuda, aga pirukatega on lugu juba kahtlasem.
Edasi võib veel nuputada, kuidas käituda, kui lisad kohvile ka piima. Mis Sa arvad, kas 15 minuti möödudes on külmem kohv, millele on lisatud kohe veidi piima, või kohv, millele lisad piima alles 15 minuti lõppedes? Newtoni seaduse ja mõne lisaeelduse abil saab vastuse välja nuputada, või lihtsalt katsetades.
Muidugi pole ennustused alati sajandiku pealt täpsed – tegelikult on soojusülekande protsess palju keerulisem ning Newtoni seadus on nagu ikka lihtsustatud kirjeldus ja kehtib ainult osaliselt. Siiski on see väga tore, et klassikaline füüsika ja veidi lihtsat matemaatikat aitavad selgitada ja ennustada igapäevaseid olukordi.
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!