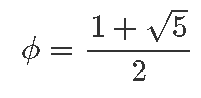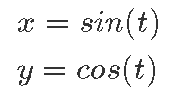Mõnel arvul on matemaatikas päris omamoodi roll. Esimese näitena tulevad pähe näiteks arvud null ja üks.

Null torkab silma, sest käitub korrutamisel ja liitmisel teistest erinevalt: korrutades mistahes arvu nulliga, saame vastuseks nulli, ning liites mistahes arvule nulli, saame sama arvu, mis enne. Samamoodi on üks isemoodi, sest korrutades ükskõik mis arvu ühega jääb see arv samaks ning ühe kõik astmed on tema endaga võrdsed.

Ajalooliselt on mainimist väärt arvuks kindlasti ka √2, mis näitas, et ratsionaalarvudest pole maailma kirjeldamiseks sugugi küllalt [lk 87].

Miks mitte välja tuua ka imaginaararvu, mille abil laiendasime reaalarve kompleksarvudele [lk 89] või iluideaaliks loetud kuldlõike arvu

[lk 135].

Käesolevas peatükis räägime aga pikemalt kahest teisest põnevast ja kuulsast arvust, millest ei saa üle ega ümber ka koolimatemaatikas. Tutvustame tegelasi: π ja e.

Pii

Arv π seostub kõigile meile ilmselt ringjoonega. Nii alustamegi arvuga π tutvumist väikese mõtisklusega ringjoonest.

Kuidas mõelda ringjoonest?

Ringjoon on ilus matemaatiline objekt, millele ei ole muidugi raske leida ka pärismaailmas vastet. Nii nagu igapäevaelus kohtame ringikujulisi objekte väga erinevates olukordades, saab ringjoonest ka matemaatiliselt mitut moodi mõelda.

Sirkli abil

Hulkade juures [lk 60] mainisime juba ühte viisi ringjoone kirjeldamiseks: ringjoont võib kirjeldada kui kõikide tasandipunktide (x;y) hulka, mis asuvad ühest välja valitud punktist (ringi keskpunktist) võrdsel kaugusel. See selgitab, miks saame ringjoont joonistada just nimelt sirkli abil.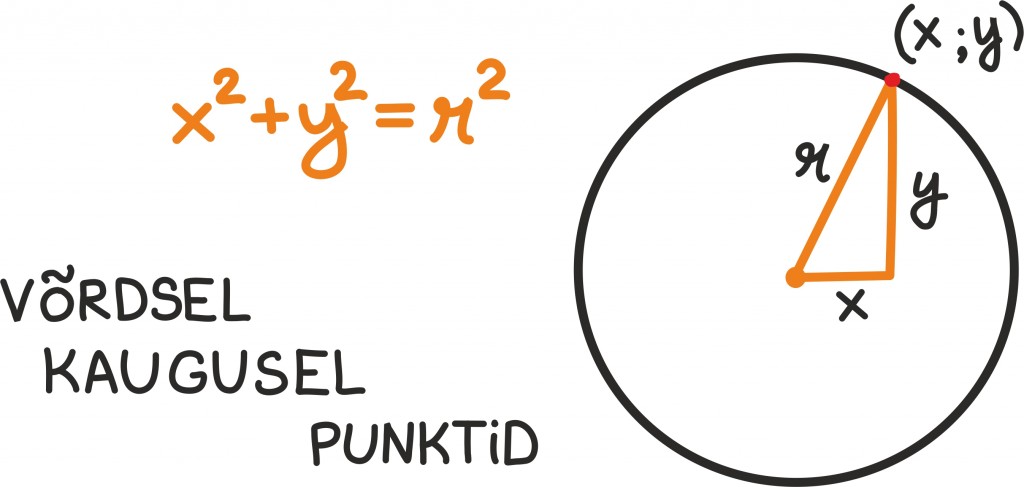 

Kõige ümmargusem

Eelnev ei ole siiski ilmselt esimene kirjeldus, mille peale mittematemaatik tuleks. Eelkõige jääb ju ringjoone juures meelde tema ümarus ja sümmeetria. Näiteks õhku tõstetud jalgratta ratast võib lõpmatult ümber tema telje pöörata ja me märkame ainult kodarate liikumist – ratas ise oleks justkui paigal.

Tuleb välja, et ka sellest vaatlusest lähtudes on võimalik ringjoon rangelt ja matemaatiliselt korrektselt defineerida: ringjoon on ainus kahemõõtmeline suletud joon, mida võime ükskõik kui palju pöörata, ilma et tema kuju muudaksime. Matemaatilisemalt: ringjoon on kõige rohkemate (pöörd)sümmeetriatega kujund.

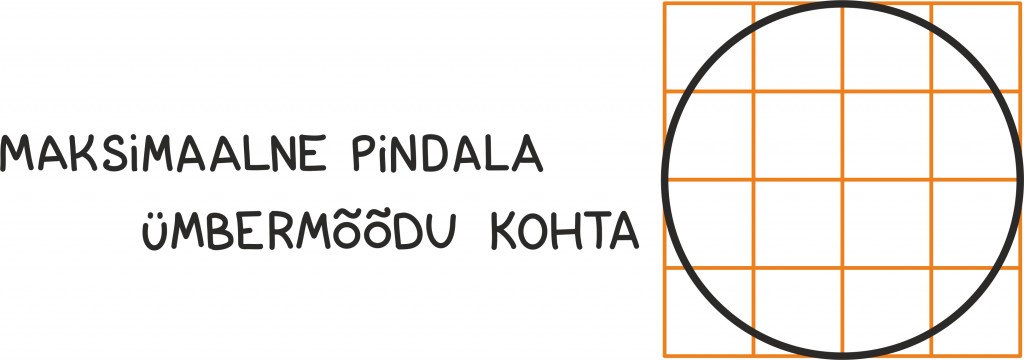
Pindala ja ümbermõõdu suhe

Kui lambakarjusel oleks vaja lammastele ehitada tara, nii et sama materjalihulga ehk ümbermõõdu korral saaks kasutada võimalikult suurt rohumaad ehk pindala, siis saab ta jällegi täiesti ausa ringi.

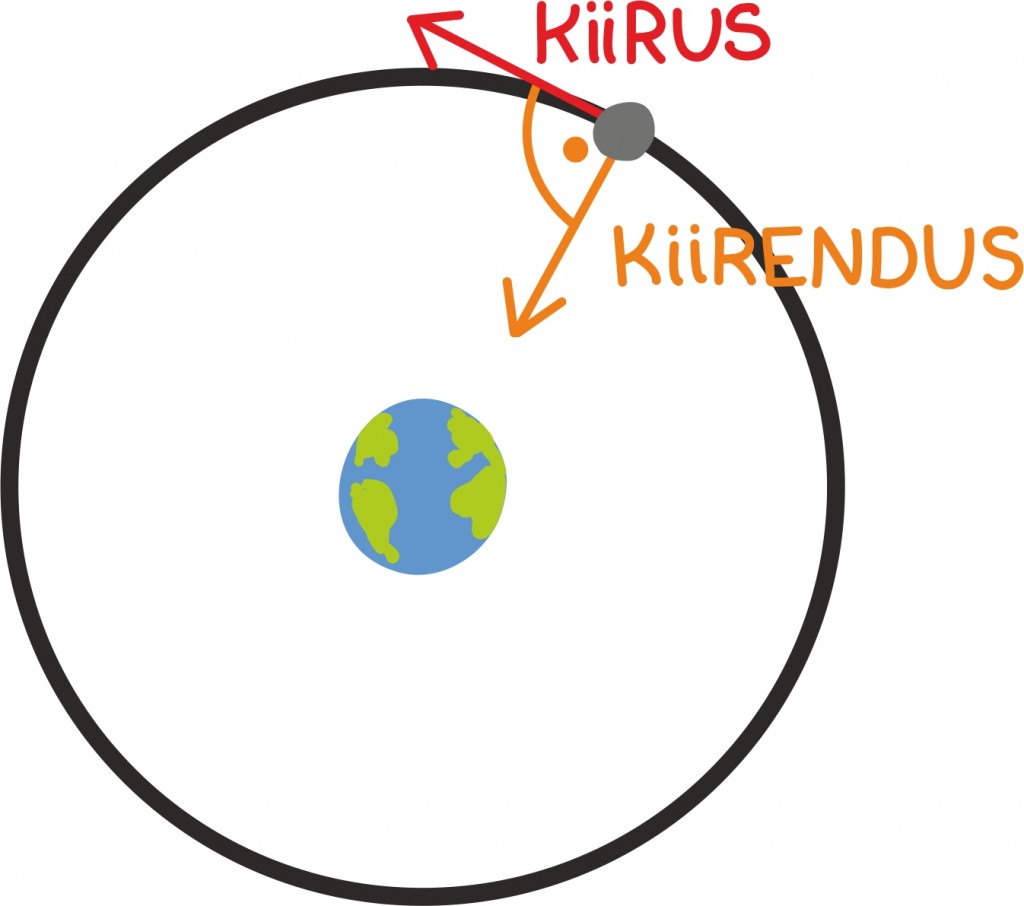
Füüsikute kombel

Füüsikud seevastu ütleksid ilmselt, et ringjoon on ainus trajektoor tasandil, mida mööda liikudes on alati kiirendus ja kiirus risti. Sel juhul muudab kiirendus ainult kiiruse suunda ja mitte tema suurust. Tekib ilus ühtlane ringliikumine.

Näiteks on enamik satelliite Maa ümber ringliikumises. Täpselt ringikujulise orbiidi tekitamiseks tuleb siiski kiirus hoolega valida. Füüsikud tulevad sellega hästi toime. Näiteks komeedid seda aga ei oska ja tiirlevad ümber Päikese väga väljaveninud ellipsit mööda.

Parameetrilise võrrandi kaudu

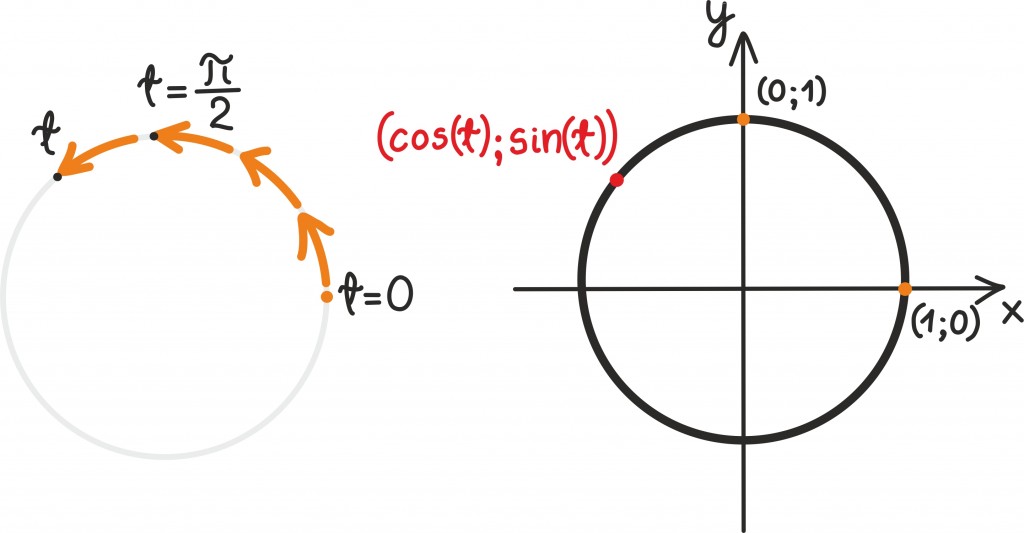
Ülikoolis matemaatikaga kokku puutudes võib aga kohtuda veel hoopis uutmoodi ringjoone definitsiooniga. Nimelt saab iga kõverjoont tasandil vaadelda kui ühe funktsiooni väärtuseid. Õigesti valitud funktsioon kirjeldab täpselt ringjoone kuju ning funktsiooni argument tähistab siis intuitiivselt lihtsalt meie asupaika ringjoonel. Ringjoone kirjeldamiseks peame kasutama funktsioone siinus ja koosinus, millest on juttu ka trigonomeetria peatükis [lk 230].

Ringjoone kõiki punkte (x;y) kirjeldava parameetrilise võrrandi saame, kui muudame funktsiooni sisendit tnullist kuni 2π-ni ning arvutame x-i ja y-i järgnevalt:

 

Nõnda saadud kirjeldust nimetatakse parameetriliseks võrrandiks.

Kõik ülaltoodud viis ringjoone definitsiooni on matemaatiliselt võrdväärsed. Seega pole vist sugugi liig öelda, et ringjoon on üks mitmekülgne ja ilus matemaatiline objekt. Ringjoon loob seoseid matemaatikas ja on kesksel kohal kogu looduse kirjeldamisel. Ringliikumine oli ideaaliks juba vanadel kreeklastel ja selle valguses on muidugi päris tore, et isegi liikluse planeerijad on otsustanud, et kõige ohutumad ristmikud on just ringristmikud.

Arvu aste