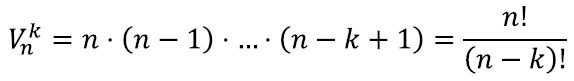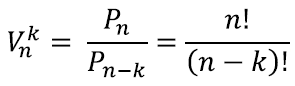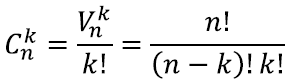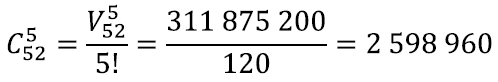Kui permutatsioonid olid seotud teatud objektide järjekorraga, siis kombinatsioonid ja variatsioonid on seotud objektide valikuga.

Üks kombinatsioon on näiteks kodupeenralt südamekaaslasele valitud kolm lillenuppu või pokkerimängus jagatud viis kindlat kaarti või kolm õpilast, kes tahvli ees vastama peavad.

Ehk teisisõnu on üks kombinatsioon kindla arvu objektide valik mingi kindla arvu objektide hulgast. Kombinatsioonide puhul valime objektid välja ilma kindla järjestuseta.

Variatsioonide puhul on samuti tegemist samasuguse objektide valikuga, aga sel juhul huvitab meid ka nende järjekord – me valime kolm õpilast, kes tahvli ees vastama peavad, ning anname neile lisaks ka vastamisjärjekorra.

Variatsioonid ja kombinatsioonid on omavahel tihedalt seotud.

Variatsioonist saame kombinatsiooni siis, kui võtame variatsiooni ning seejärel unustame elementide järjekorra. Näiteks õpetaja võib tunni jaoks välja valida kolm järjestikust vastajat, seejärel ümber mõelda ja lasta neil korraga kirjalikult vastata, nii et järjekorral ei ole enam tähtsust.

Kombinatsioonist saame aga variatsiooni, kui võtame ühe kombinatsiooni ning siis anname valitud elementidele ka järjekorra. Näiteks õpetaja võib valida kolm vastajat ja siis anda neile vastamisjärjekorra.

Kombinatsioonide ja variatsioonide arv

Pokkerihaisid (kui nad tahavad olla ohtlikud haid) huvitab muidugi, kui palju leidub erinevaid pokkerikäsi ühest pakist – see võimaldab näiteks arvutada, kui suur on tõenäosus, et mõnel teisel sõbral lauas on paremad kaardid.

Kui mängid pokkerit, kus igale mängijale jagatakse viis kaarti, huvitab meid 5-kaardiste kombinatsioonide arv 52 kaardi hulgast. Seda arvu tähistatakse

Üldisemalt tähendabki

või

võimaluste arvu valida n objekti hulgast k erinevat.

Näiteks leidub

erinevat pokkerikätt.

Variatsioonide arvu tähistatakse omakorda

Näiteks kui tahaksime mingil põhjusel leida kõikvõimalike järjestatud pokkerikäte arvu, siis võib arvutada:

Väikeste arvude korral võime kõik kombinatsioonid ja variatsioonid muidugi üles lugeda, aga nagu nägime, on juba pokkerikäte korral tegemist päris suurte arvudega ning neid järjest lauale seades võime märkamatult päris vanaks saada.

Seega üritame järgnevalt mõelda, kuidas leida kombinatsioonide ja variatsioonide arvu kõiki võimalusi läbi vaatamata.

Variatsioonide arv

Leiame kõigepealt variatsioonide arvu. Arutelu on analoogne permutatsioonide arvu leidmisega – järjestuse esimese kolme elemendi kindlaks määramine ongi ju täpselt kolme järjestatud elemendi väljavalimine.

Ehk siis kui meil on näiteks vaja valida 5 järjestatud kaarti 52-st, siis valime nad ükshaaval, järgemööda. Esimese valik on täpselt 52 võimalust, teise valikuks jääb siis 51 võimalust, kolmanda valikuks 50, neljanda valikuks 49 ja viienda valikuks 48 võimalust. Kuna kõik valikud on sõltumatud, näeme, et

mis annab tõesti arvu 311 875 200.

Üldjuhul saame siis samasuguse arutelu abil, et

Selle korrutise võime ka faktoriaalide abil kirja panna: murru lugejasse seame kogu korrutise ning murru nimetaja abil taandame ära korrutise lõpuosa:

Tegelikult oleksime võinud variatsioonide arvu leidmiseks kasutada ka teistsugust arutelu ja lähtuda otse permutatsioonide arvust. Nimelt n-elemendi reastamisest (ehk ühest permutatsioonist) võime mõelda järgmiselt:

1. Kõigepealt seame ritta mingid k esimest elementi ehk valime n elemendist k elementi, arvestades ka järjekorda, milleks ongi variatsioon:
   
2. Seejärel reastame sinna järele kõik ülejäänud n –k elementi ehk valime permutatsiooni: P_n–k

Kuna need sammud on sõltumatud, on n-permutatsioonide arv kokku

ehk

See annabki aga täpselt eelmise valemi, seekord koos intuitiivse selgitusega.

Kombinatsioonide arv

Leidmaks lõpetuseks kombinatsioonide arvu, tuletame meelde enne mainitud seose kombinatsioonide ja variatsioonide vahel: igast k-variatsioonist võime teha k-kombinatsiooni, kui elementide järjekorra ära unustame.

k-elemendi järjekordade arv on aga täpselt võrdne permutatsioonide arvuga k!. Seega on iga kombinatsiooniga seotud täpselt k! erinevat variatsiooni. Nii peame kombinatsioonide arvu saamiseks jagama variatsioonide arvuga k! ehk

Eelmises alapeatükis leidsime, et 5 kaardi võtmiseks (kui järjekord on oluline) on meil

võimalust.

Kui meil on 5 kaarti, siis kaartide permutatsioon näitab erinevaid võimalusi nende kaartide järjestamiseks, milleks on 5! = 120.

Kui järjekord ei ole tähtis, siis kokku on kaardipakist 5 kaardi võtmiseks

võimalust.

Tõenäosusteooria tähendus ja kasutamine