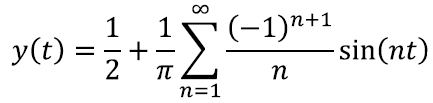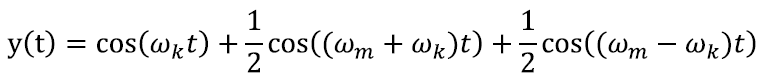Kõik võngub*

Harva on asjad tasakaalus, ikka kipuvad nad minema veidi paremaks ja siis jälle veidi halvemaks ja nii edasi. Füüsikud kirjeldavad sellist korduvat tasakaaluasendi ümber toimuvat pendeldamist sõnaga võnkumine. Meie ümber võib märgata palju ilusaid võnkumisi: kiiged, pendlid, vedrud, helikeeled ja nii edasi. Võnkumise matemaatiliseks kirjelduseks kasutame perioodilisi funktsioone. Siinus- ja koosinusfunktsioon on ilmselt kõige ilusamad näited perioodilistest funktsioonidest. Nagu elastse vedru näite juures nägime [lk 236], kirjeldavad nad mingis mõttes kõige lihtsamaid ja loomulikumaid võnkumisi. Kuna need võnkumised on kõige levinumad ja üpris ilusad, kutsutakse neid ka harmoonilisteks võnkumisteks.

Kuigi trigonomeetriliste funktsioonide sin(t) ja cos(t) periood on alati sama – täpselt 2π –, võime otsustada nurka ka kiiremini või aeglasemalt muuta ning seega kirjeldada kiiremaid ja aeglasemaid harmoonilisi võnkumisi. Nägime seda juba ka vedru juures [lk 236], kus olenevalt vedru omadustest olid lahendiks kiiremad või aeglasemad harmoonilised võnkumised.

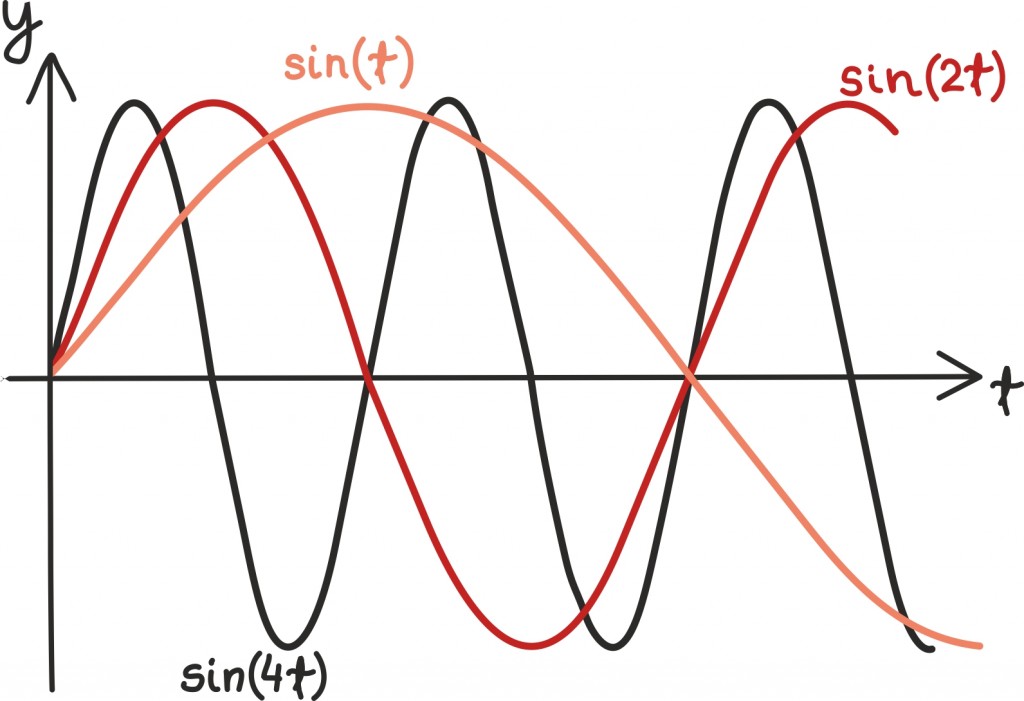
Funktsiooni sin(t) asemel võime nii vaadata ka funktsioone sin(2t) või sin(4t), mille perioodid on vastavalt kaks ja neli korda väiksemad.

Funktsioonid kujus sin(nt) ning cos(nt), kus n on positiivne täisarv, kirjeldavad kõiki siinus- ja koosinusfunktsioone, mis läbivad vahemikus [0,2π] täpselt täisarvu täisperioode.

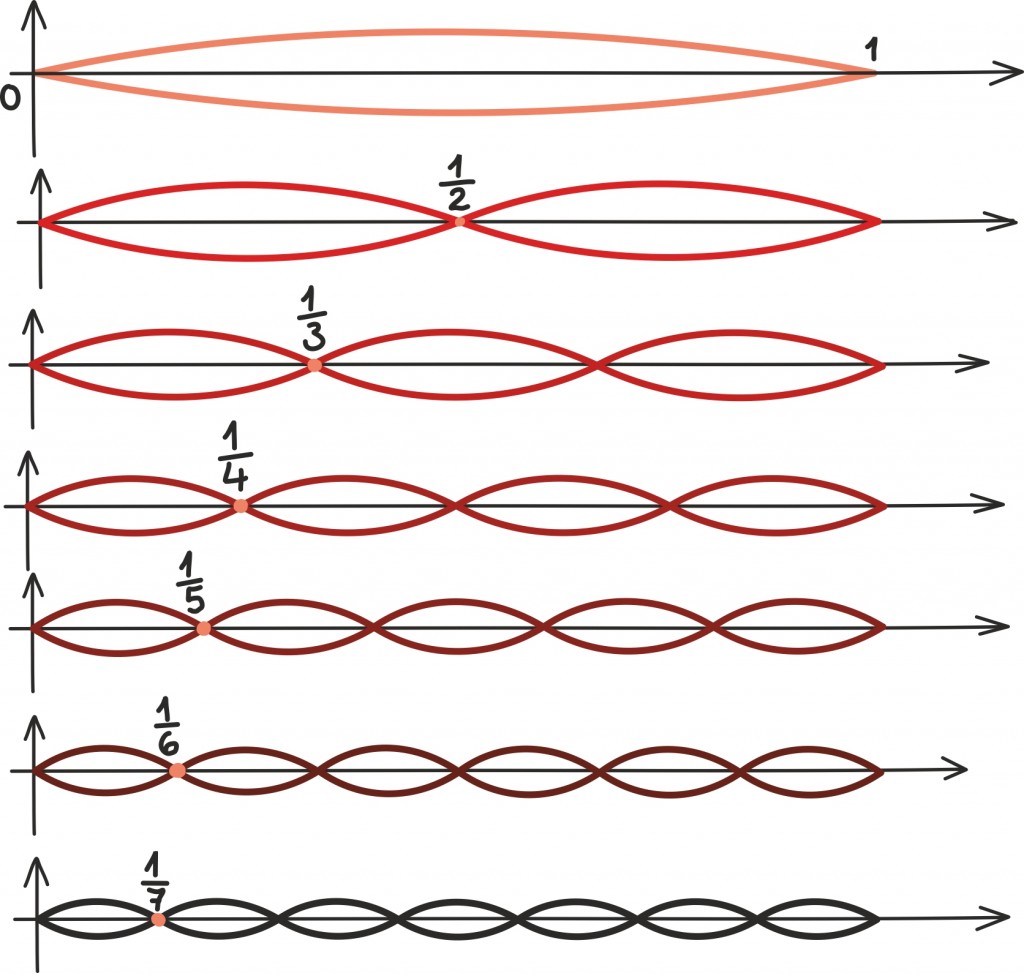
Sellised funktsioonid kirjeldavad ühe otstest kinnitatud pillikeele kõiki erinevaid põhivõnkumisi ehk osahelisid. Nende võnkumiste sagedused (ehk kui mitu täisperioodi nad läbivad) annavad kõik põhivõnkesagedused.

Nagu muusikast teame, võime iga liitheli või akordi lahti kirjutada osahelidena. Samamoodi selgub, et tegelikult võime iga piisavalt ilusa perioodilise funktsiooni esitada põhivõnkumiste summana. Eri põhivõnkumisi tuleb erinevate funktsioonide esitamiseks muidugi kasutusele võtta erineval määral.

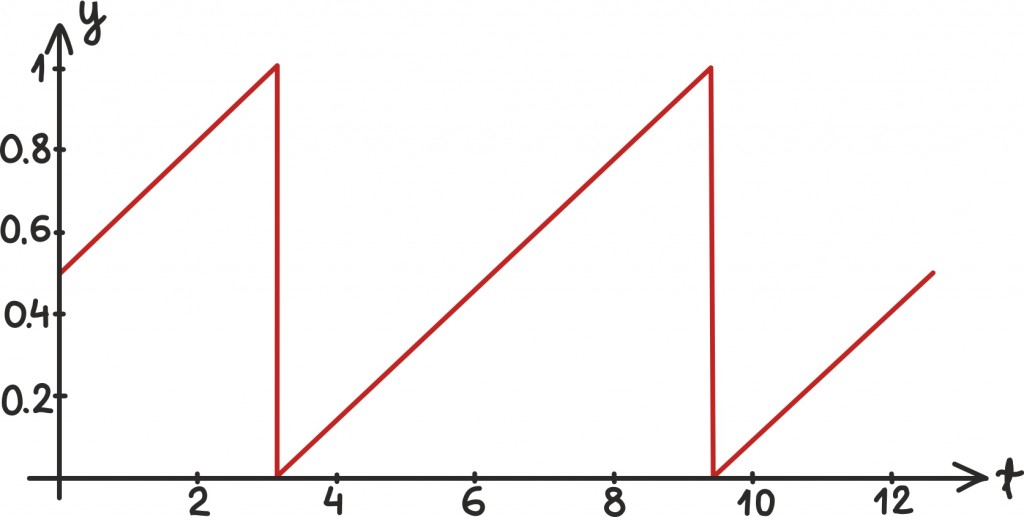
Sellist perioodiliste funktsioonide esitamist põhivõngete abil nimetatakse nende Fourier’ esituseks. Vaatame näiteks niinimetatud saehamba funktsiooni:

Ettevaatlikuks peaks muidugi tegema asjaolu, et funktsiooni graafikul asuvad vertikaalsed jooned. Nii jääb mulje, nagu kohtadel π ja 3π ja nii edasi oleks funktsioonil lõpmatult palju väärtuseid, aga ometigi on definitsiooni järgi funktsioonil igale kohale lubatud vaid üks väärtus [lk 64]. Ja kõik on õige, teemegi siin natuke haltuurat, õigupoolest on saehamba funktsioon nendes kohtades võrdne täpselt poolega, aga see näeks hoopis koledam välja.

Saehamba Fourier’ esitus ehk lahtikirjutus võnkumiste summana on järgmine keeruline moodustis:

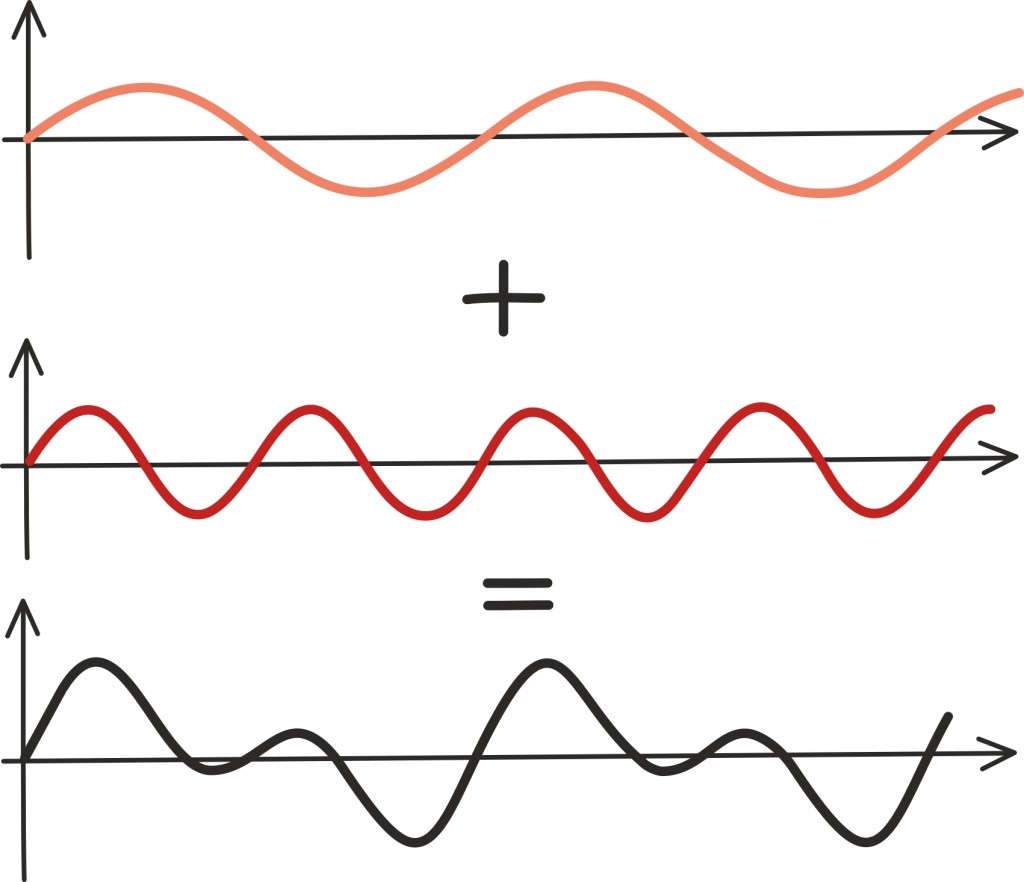
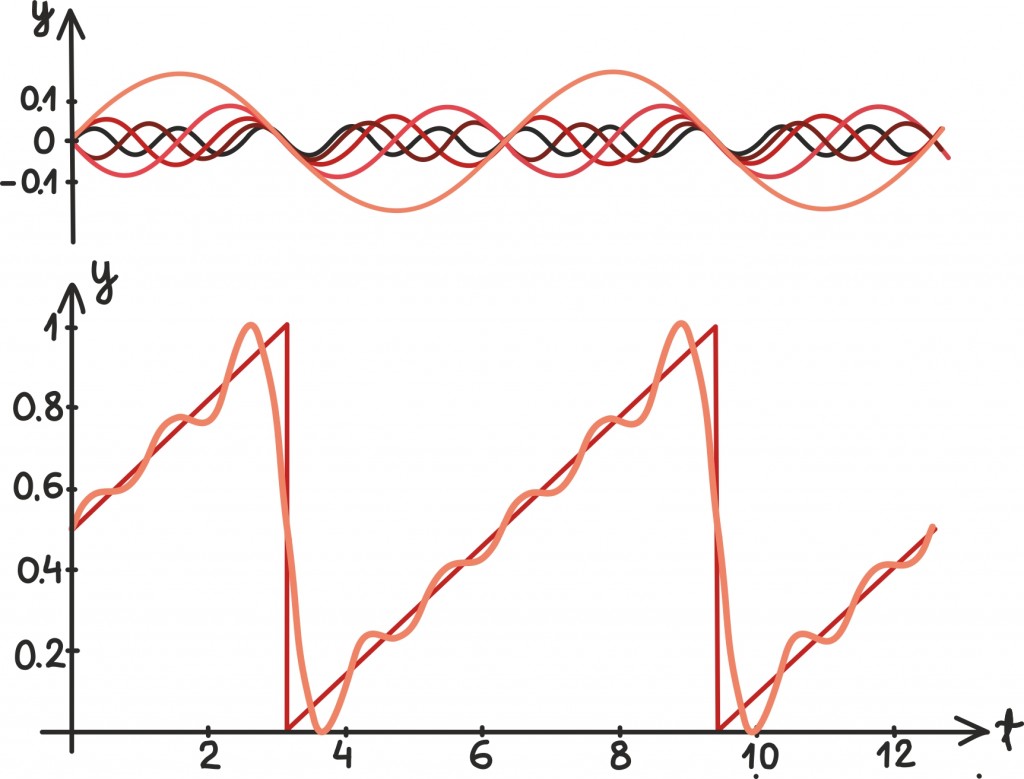
Nagu näeme, peab aeglaseid võnkumisi võtma suuremal määral kui kiiremaid – kordaja siinusfunktsioonide ees ju aina kahaneb. Järgmisel joonisel näitame kõigepealt viit esimest siinusfunktsiooni oma kordajatega. Seejärel liidame nad kokku, paneme veel juurde pool ning saamegi midagi üsna saehamba sarnast:

Mida rohkem siinusfunktsioone kokku liidame, seda sarnasem on tulemus ka saehambaga. Nagu näeme, ei tea ka meie lihtne lähendus saehambale, kas olla π juures väärtusega üks või null.

Fourier’ esitus ja spekter

Fourier’ esitus pakub hea vaatevinkli signaalide ja protsesside uurimiseks. Fourier’ esitus paneb teatud mõttes tööle analoograadiod, võimaldab leida kosmilisi objekte ning teha automaatset pilditöötlust.

Kogu asja võlu seisneb lihtsustatult selles, et teatud signaalidest on palju lihtsam aru saada, kui mitte vaadata nende arengut ajas, vaid uurida, kui palju üht või teist põhivõnkumist signaali kirjeldamiseks kasutama peab. Tihti on see ka ainus loomulik vaateviis. Funktsiooni Fourier’ esitust saab näidata graafiliselt nii-öelda spektri abil: spekter näitab täpselt, kui suure osa signaalist moodustab üks või teine põhivõnkumine.

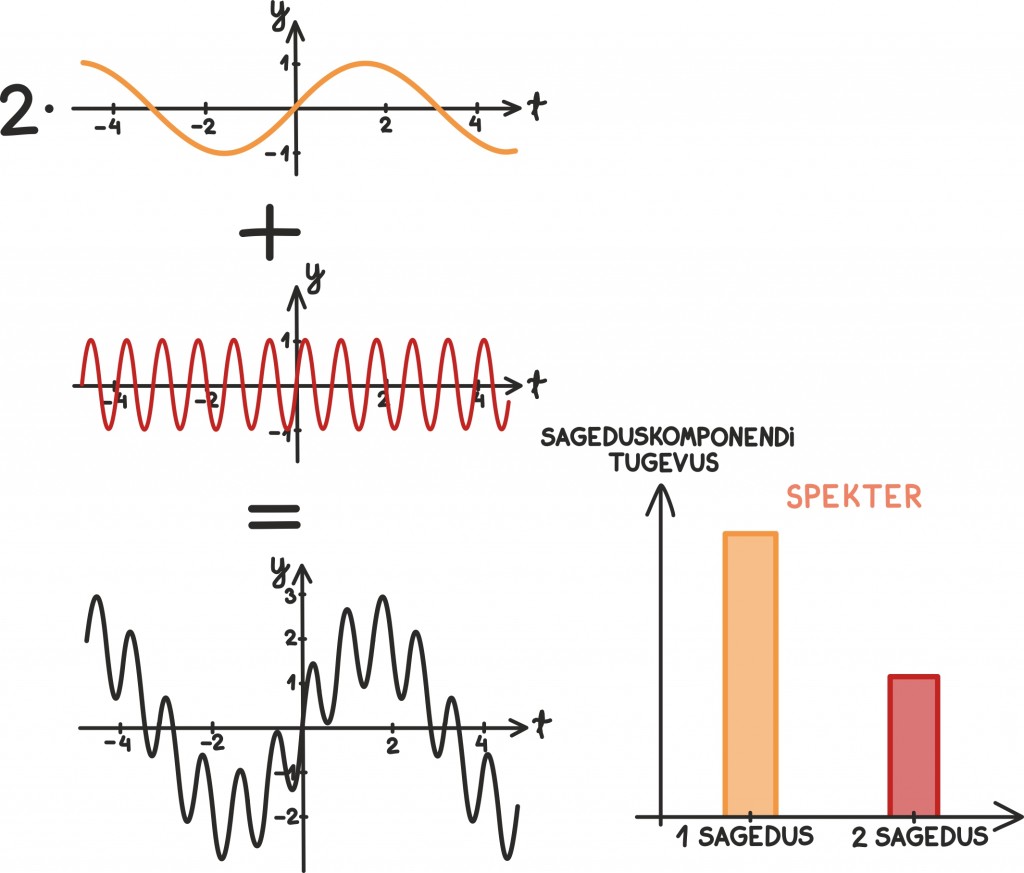
Näiteks järgnevalt võtame kaks võnkumist, ühe madalamal ja teise kõrgemal sagedusel. Seejärel leiame signaali, milles esimese võnkumise amplituud on kaks, teise amplituud aga üks. Kogu see informatsioon ongi kompaktselt kirjas joonisel paremal all nurgas olevas spektris.

Tavaliselt on muidugi sagedused ka täpsete arvuliste väärtustega ning sageduskomponendid näitavad iga osavõnkumise amplituudi. Need on aga juba detailid.

Toome järgnevalt ka näite, kus signaali esitamisest võnkumiste summana võiks ka otseselt kasu olla.

Kuidas kaob helisalvestisest sahin

Oletame, et otsustad sõbrale sünnipäevaks ühe omamoodi sünnipäevalaulu lindistada. Mikrofon on olemas, arvuti ka ja lindistamine ise ei valmista mingeid muresid.

Ometigi jääb salvestisele tugev sahin. Kas sellest on võimalik kuidagi lahti saada?

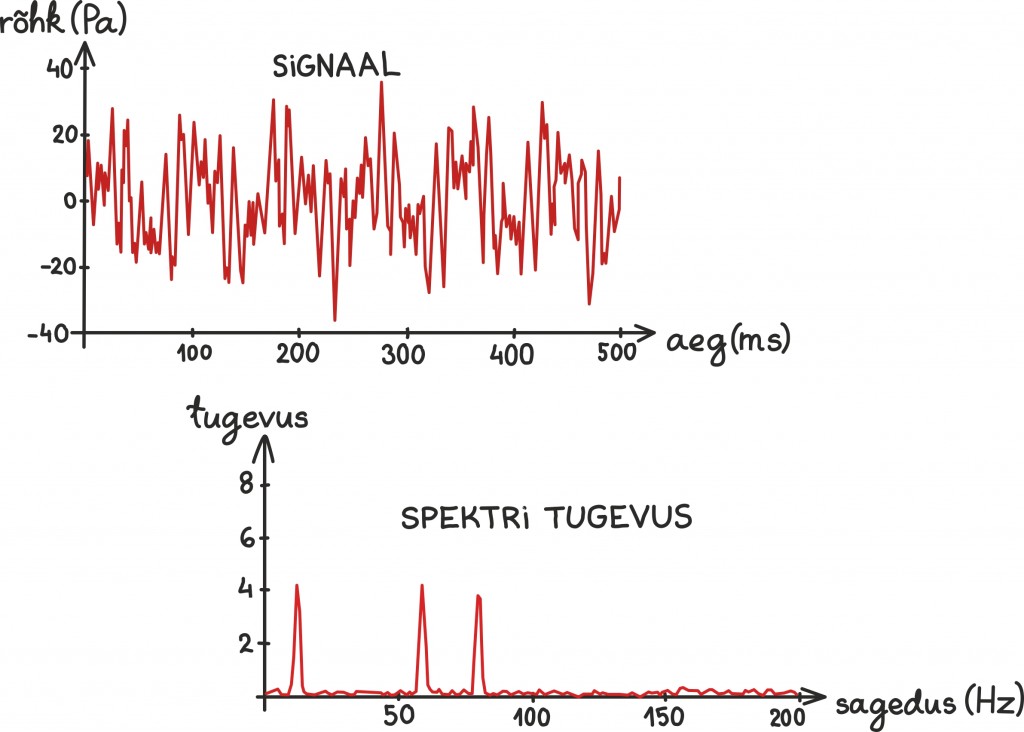
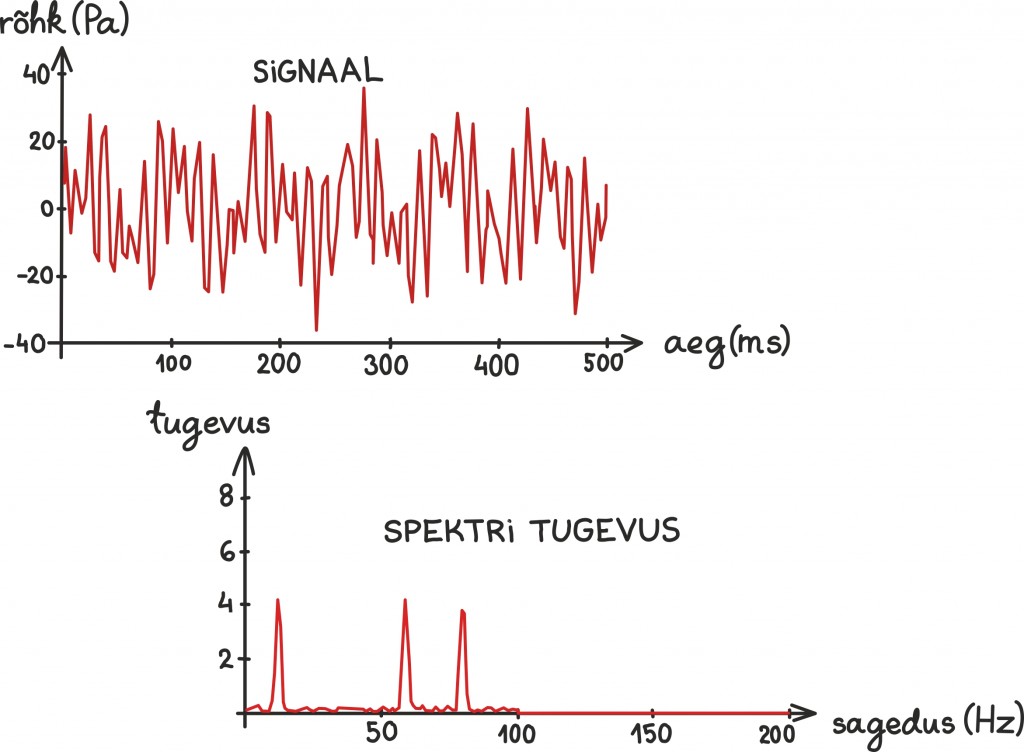
Võtmetähelepanek on järgmine: sahin on tihti seotud eelkõige üleliigsete kiirete võnkumistega. Ehk teisisõnu, kui vaatame oma salvestist tema Fourier’ esituses ehk võngete summana, siis on sahin sinna suurel määral salvestunud väga kõrge sagedusega komponentidesse.

Kuna laul ise koosneb põhiliselt hoopis väiksema sagedusega võngetest, on Fourier’ esituses sahin ja hääl teatud mõttes eraldatud. Seda näeme spektrist, kust häälele vastavad eelkõige need kõrged tipud spektri vasemal ja sahin on paremale jääv madal osa.

Nüüd võime sahina komponendi Fourier’ esituses ära kustutada ja ülejäänu jälle kokku liita. Saame uue signaali, mis kannab peaaegu kõiki häälega kaasas käivaid võnkumisi, kuid ei sisalda enam sahinat ja kõlab seega puhtamalt. Uus signaal ja tema spekter näevad välja järgmised:

Umbes nii töötavadki digitaalsed filtrid näiteks muusikaloomeprogrammides. Kas pole kaval?

Sulle võivad huvi pakkuda need õppematerjalid:

AM-raadio

Võnkumise levimisprotsessi ruumis kutsutakse laineks. Helilised võnkumised levivad helilainetena. Oma vestluse ja muusika kaugele sõbrale saatmine oli vanasti päris keeruline – lihtsalt suuga teele saadetud helilained eriti kaugele ei ulatu.

Kaval viis helilainete edastamiseks on teisendada nad elektromagnetlaineteks ning hoopis neid edasi saata. Aga sealgi on omad raskused. Näiteks on kohe probleemiks see, et meie hääl ja muusika on madalal sagedusel ning madalsageduslike elektromagnetlainete saatmiseks peab olema kilomeetrite pikkune antenn! Teine probleem tuleb sellest, et samal ajal tahaksime võibolla ringi saata väga erinevat sisu ja kui need oleksid kõik salvestatud sama sagedusega elektromagnetlainetesse, seguneksid sisud omavahel ja välja tuleks mingi tohuvabohu. Seega on hea raadiosüsteemi väljatöötamine parajalt keeruline.

Õnneks on alati leidunud nupukaid selle, kes keerulistele olukordadele lahenduse leiavad. Toodud muredest lahti saamiseks hakati raadiosignaale edastama niiöelda moduleerimise teel – madalsageduslik sisu salvestati väga kõrgsageduslikele lainetele. Esiteks saab selliseid laineid saata ja vastu võtta täitsa mõistliku antenniga. Teiseks tuleb välja, et nii võime paralleelselt saata ka väga palju erinevaid signaale.

Kõige lihtsam neist moduleerimise tehnoloogiatest, AM ehk amplituudi modulatsioon on lähedalt seotud tähelepanekuga, et trigonomeetriliste funktsioonide korrutise võib lahti kirjutada nende summana ning vastupidi. Amplituudi modulatsioon ei tähenda seejuures midagi muud kui seda, et ühe laine amplituudi muudetakse teise laine abil. Seeläbi salvestatakse algsesse lainesse informatsiooni.

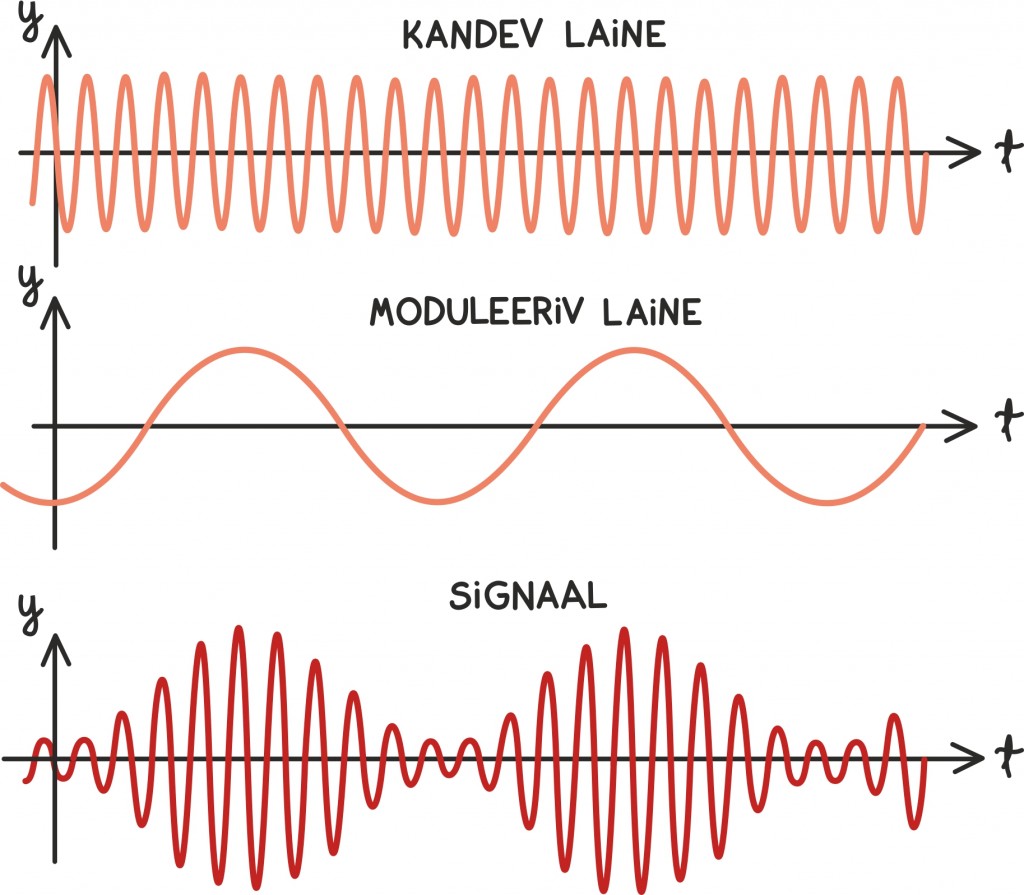
Lihtsustatult võib mõelda, et saatjast teelepandav raadiosignaal y(t) koosneb ühest kandvast lainest kõrgel sagedusel ω_k. Kui tahame talle informatsiooni külge pookida, muudame kandva laine amplituudi mingi madalama sagedusega laine abil.

Näiteks kui sagedusega ω_k liigub kandev laine, mille amplituudi muudetakse koosinuselainega sageduselω_m, siis võiks kogu signaal olla kujus:

Kuna trigonomeetriliste funktsioonide korrutise võime lahti kirjutada ka nende summana [lk 250], võime signaali samas näha ka kui eraldiseisvate lainete kooslust:

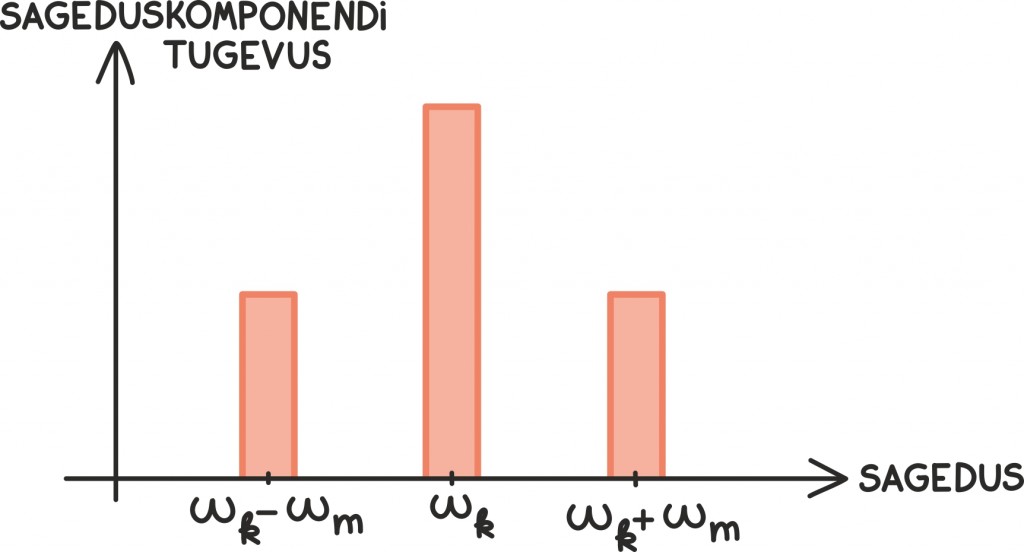
Teisisõnu, meie signaal koosneb kolme laine summast: kandvast lainest ja kahest lisalainest.

Nende lainete taga peidus olevate võnkumiste sagedusesitus ehk spekter oleks siis järgmine:

Need lisalained või lisavõnkumised saab nüüd vastuvõtjas Fourier’ teisenduse [lk 257] abil eraldada, just nii nagu sahina eraldamiselgi. Seeläbi õnnestub meil kandvale lainele lisatud signaal vastuvõtjas välja lugeda!

Veelgi enam, kui meie kandev laine on näiteks sagedusel 1000 kHz ja sisuks on signaal alla 5 kHz, siis mahub ju kogu signaal ehk kõik kasutatavad lainekomponendid 995 kHz ja 1005 kHz vahele. Seega juba sagedusega 1020 kHz kandelainel võiksime julgelt paralleelselt teise sisuga signaali edastada – kasutatavad lained ei kattuks ja neid saaks ilusasti vastuvõtjas eraldatult välja lugeda.

Muidugi on kandelainele lisatav sisu enamasti palju keerulisem kui üks pisike laine ning lisaks muutub ta veel ajas, ent põhimõte jääb samaks: saatjas lisatakse informatsioon kandjalaine amplituudi muutmise teel ning vastuvõtjas saadakse see signaali komponentideks jagamise abil taas kätte.

Siinkohal sai küll kirjeldus kiire ning ebatäpne, aga huvi korral uurige, see on päris põnev! Tõtt-öelda on muidugi AM-raadio juba üsna iganenud tehnoloogia. Tänaseks on pigem kasutusel niinimetatud FM-raadio, kus muudetakse hoopis kandva laine sagedust, mitte amplituudi. Ja juba varsti minnakse ilmselt kõikjal üle digitaalsete signaalide edastamisele. See jääb aga kahjuks siit raamatust väljapoole.

Polünoom