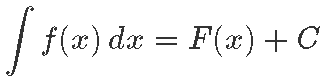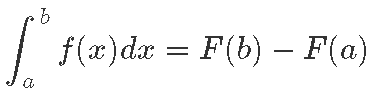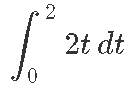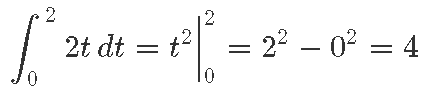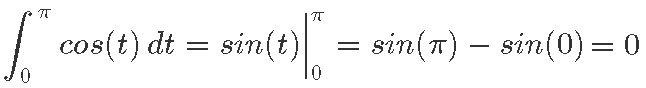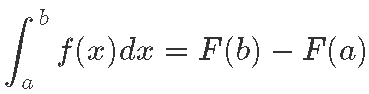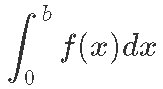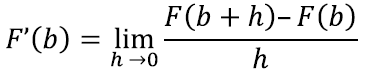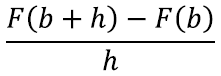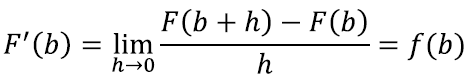Integraal ja tuletis

Pöördoperatsioonid on matemaatikas üsna levinud. Kõige lihtsam näide tulebki võibolla pööretest endast: kui pöörame oma joonist tasandil 90 kraadi päripäeva, siis teda seejärel 90 kraadi vastupäeva keerates on ta jälle algseisus tagasi. Samuti võime liitmisest ja lahutamisest mõelda kui pöördoperatsioonidest: kui liidame mõnele arvule kolm ja siis jälle lahutame, jõuame algpunkti tagasi.

Teineteisele vastupidiselt käituvad ka integraal ja tuletis. Näiteks võib mõelda, et tuletis arvutab funktsiooni muutumise kiirust, integraal aga liidab funktsiooni muute kokku.

Liikumise kirjeldamise korral on lugu näiteks järgmine:

tuletis annab meile etteantud tee pikkuse abil liikumise kiiruse
ning integraal arvutab liikumise kiiruse põhjal omakorda läbitud tee pikkuse

Seega on tõesti tegemist justkui teineteise pöördoperatsioonidega. Täpne seos integraali ja tuletise vahel on ainult veidi segasem, veidi tähelepanu vajab näiteks määratud ja määramata integraali eristus.

Tuletise ja integraali seos on ka praktiliselt kasulik. Ühelt poolt on kasu puhtalt arvutuslik: võime integraalide leidmise taandada tuletise teadmisele ja vastupidi. Teisalt annab see seos teatava mõttelise aluse üsna suurele osale looduse kirjeldamisest: selle jaoks, et kirjeldada mingi suuruse kogumuutu ehk integraali ajas, piisab sellest, kui kirjeldame tema hetkelist muutumise kiirust ehk tuletist. Selle lihtsa mõtte rakenduseks on diferentsiaalvõrrandid, mis panevad aluse suurele osale klassikalisest füüsikast. Neil me siiski pikemalt ei peatu.

Algfunktsioon ja määramata integraal

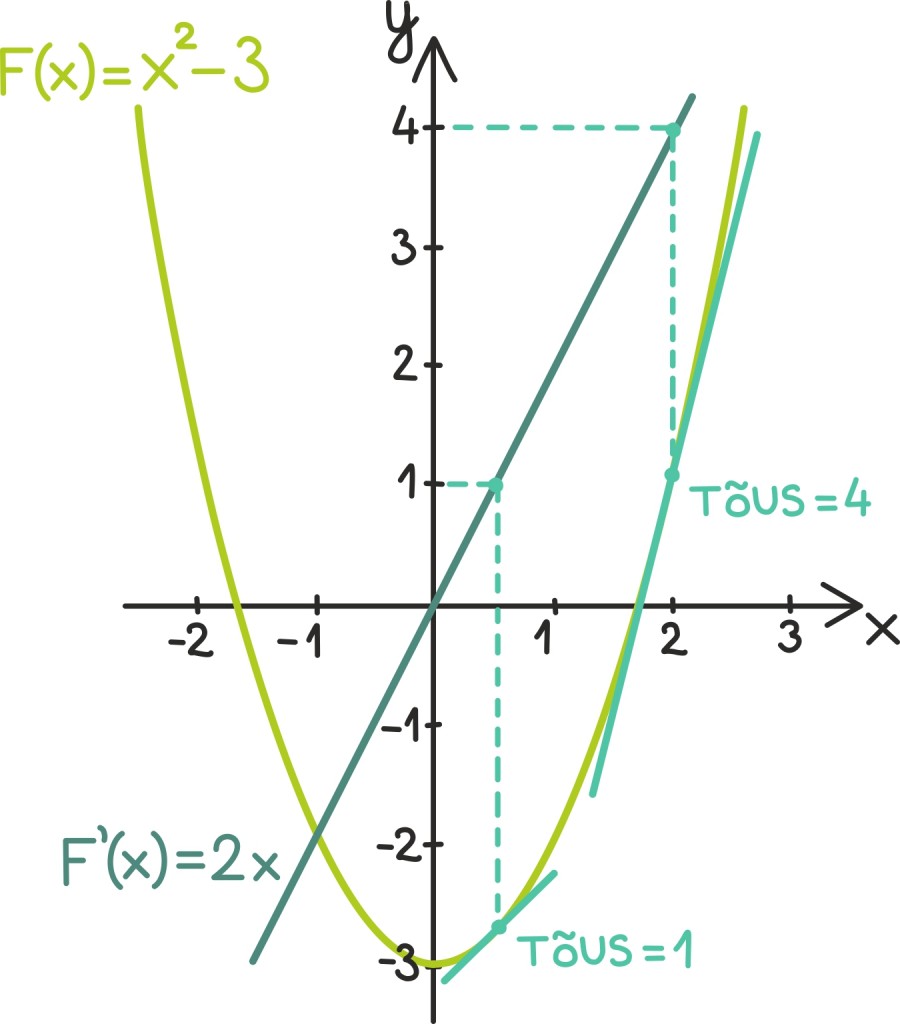
Meenutame, et kui meile on antud piisavalt sile funktsioon, millele saame igas punktis tuletise leida, võime tuletisest mõelda kui teisendusest, mis seab ühe funktsiooniga F(x) vastavusse tema tuletise funktsiooni F’(x).

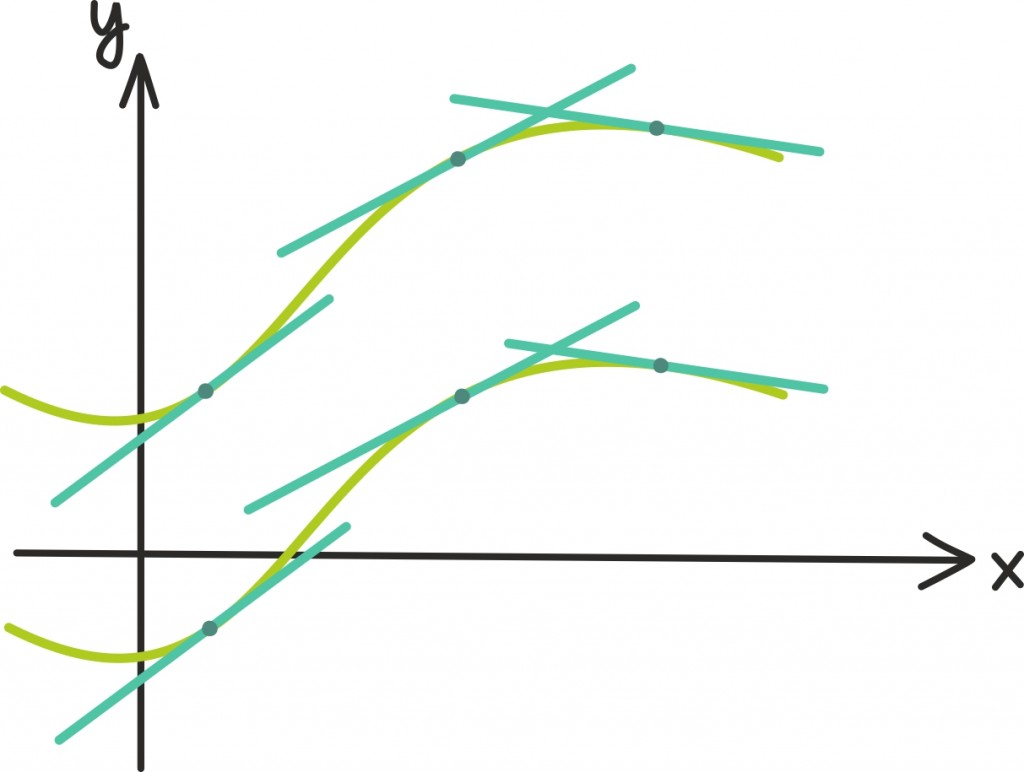
Nagu mäletame, tähendab see geomeetriliselt, et sinine graafik on kokku pandud helerohelise graafiku puutujasirgete tõusudest:

Nüüd võib mõelda ka selle teisenduse pöördteisendusele – ehk küsida, mis juhtub siis, kui tahaksime hoopis alustada sinisest joonisest ja leida funktsiooni, mille graafiku puutujatõusudest moodustuks see sinine joon?

Teisisõnu tahaksime leida funktsiooni, mille jaoks igas punktis kehtib F’(x) = ƒ(x).

Iga võimalikku vastust sellele nimetatakse funktsiooni ƒ(x) algfunktsiooniks ning mitmust kasutame siin üsna asjakohaselt – võimalikke vastuseid on palju!

Tõepoolest, kui F(x) on mõne funktsiooni ƒ(x) algfunktsioon, siis on seda ka F(x) + C iga konstandi C jaoks. Konstandi C lisamine ju ainult nihutab funktsiooni F(x) üles-alla, ent ei muuda tema muutumise kiirust – puutujad jäävad paralleelseks. Õigupoolest tuleb välja, et midagi muud teha ei võigi – kõikvõimalikud algfunktsioonid saamegi ühteainsat üles-alla nihutades.

Nüüd funktsiooni ƒ(x) määramata integraal kogubki kõikvõimalikud vastused ehk teisisõnu algfunktsioonid ühte ja samasse avaldisse F(x) + C. Siin F(x) tähistab ühte võimalikest algfunktsioonidest ning C suvalist konstanti. Määramata integraali tähiseks on integraali kõverik ilma ülemise ja alumise rajata. Seega kirjutaksime:

Sulle võivad huvi pakkuda need õppematerjalid:

Algfunktsioon ja määratud integraal

Algfunktsioonide abil võiksime tegelikult defineerida ka määratud integraali.

Nimelt võiksime öelda, et funktsiooni ƒ(x) määratud integraal vahemikus [a; b] on võrdne mõne tema algfunktsiooni muuduga selles vahemikus. Ehk siis:

kus jällegi F(x) on üks ƒ(x) suvaliselt valitud algfunktsioon.

Oluline on märgata, et sellest, millise algfunktsiooni me valime, väärtus ei muutu. Tõepoolest, konstant taandub ju lahutamistehtes välja. Geomeetriliselt mõeldes: kui nihutame funktsiooni F(x) graafikut, nihutame võrdselt nii tema väärtust vahemiku alg- kui lõpppunktis, nende vahe jääb samaks.

Integreerimine tuletise abil

Leitud seosest saame ka üsna lihtsa viisi integreerimiseks – meil on vaja lihtsalt ära arvata vastav algfunktsioon ehk tunda tuletisi!

Tõepoolest, näiteks integraali peatükis käsitletud integraali

leidmiseks piisab teadmisest, et lineaarfunktsiooni 2t üheks algfunktsiooniks on t².

Seejärel võime kirjutada

Või näiteks, kuna siinusfunktsiooni tuletiseks on koosinusfunktsioon, võiksime kirjutada:

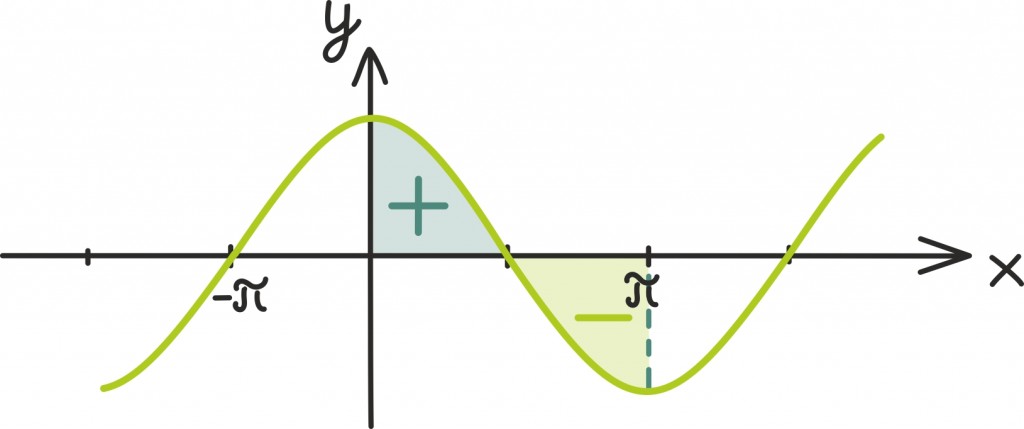
Seda on muidugi võimalik näha ka graafikult, teades koosinusfunktsiooni sümmeetrilisust ja meenutades, et x-telje alla jääv pindala näitab negatiivset kogumuutu:

Newtoni-Leibinizi seos

Newtoni-Leibnizi seoseks nimetatakse juba toodud seost funktsiooni ƒ(x), tema määratud integraali ning algfunktsiooni muudu vahel:

See ongi kõige täpsem ja kasulikum sõnastus integraali ja tuletise vahelisele seosele. Selle seose alusepanijad Isaac Newton ja Gottfried Leibniz ei suutnud omavahel kuidagi kokku leppida, kumb on ikkagi rohkem tunnustust ära teeninud. Mõlemad pidasid just oma panust olulisemaks ja nii nad jäidki Leibnizi surmani tülli. Üsna tühine tüli ilusa matemaatika ümber.

Kui määratud integraal ise selle kurikuulsa seose kaudu defineerida, ei ole seda seost muidugi vaja tõestada, tegemist oleks pigem siis seaduse või aksioomiga.

Samas ei ole ju sugugi selge, miks peaks selle seose kaudu defineeritud määratud integraal ikkagi olema seotud pindalade ning nende jupitamisega.

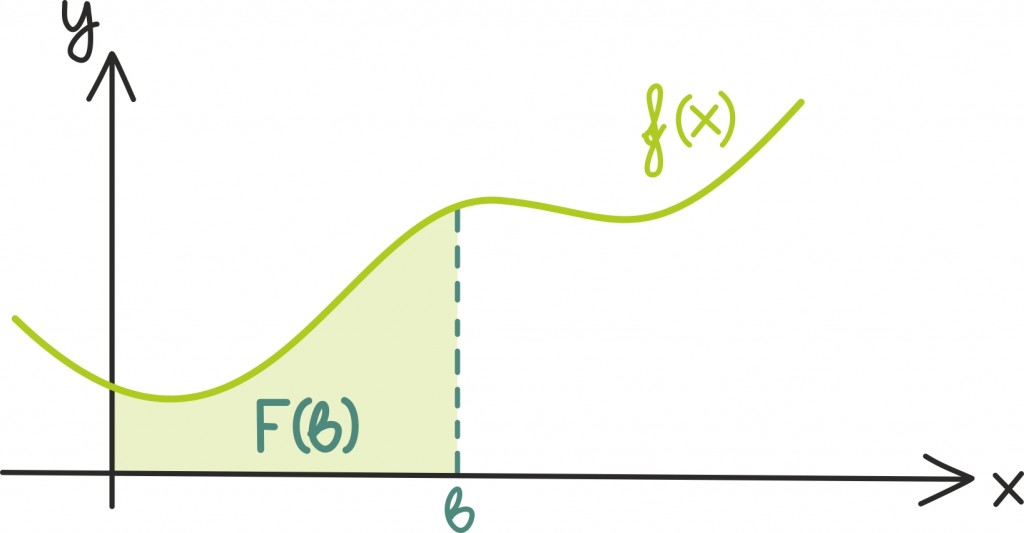
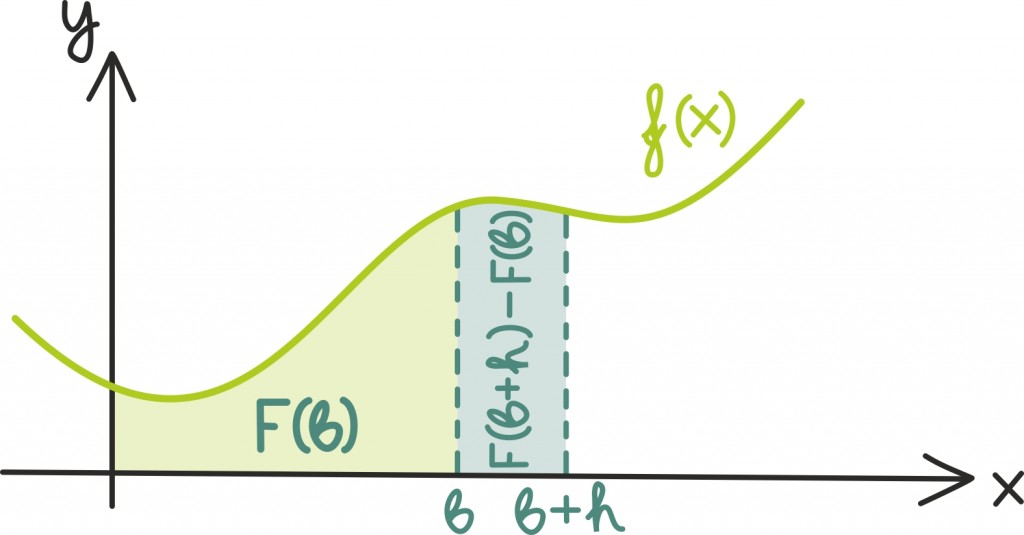
Seose olemasolus on kõige lihtsam ennast veenda geomeetriliselt. Vaatame näiteks ühte ilusat pidevat funktsiooni ƒ(x) vahemikus [0; b] ja alustame teadmisest, et määratud integraal

annab meile ƒ(x) graafiku ning x-telje vahele jääva pinnatüki pindalaga kuni punktini b. Tähistame seda pindala F(b)-ga.

Funktsiooni F(x) tuletis punktis b tähendab nüüd pindala hetkemuutu. Tuletame meelde definitsiooni:

Geomeetriliselt võime murru lugejast seega mõelda kui funktsiooni ƒ(x) graafiku alla jäävate pindalade vahest vastavalt punktideni b + h ja b:

Ehk siis parempoolse osa pindala on F(b + h) – F(b). Väga väikese h väärtuse jaoks on aga see pindalade vahe peaaegu nagu ristkülik. Seega kuna ristküliku laiuseks on h ise, siis annab jagatis

meile ristküliku kõrguse.

Mis aga on see kõrgus? Jooniselt näeme, et kõrguseks on funktsiooni ƒ väärtus b ja b + h vahel. Kui h väärtus muuta lõpmatult väikeseks, siis saab sellest muidugi ƒ-i väärtus kohal b ise. Nii näemegi, et