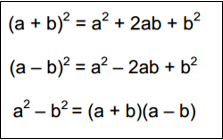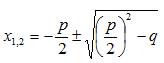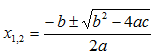HULKLIIKME TEGURDAMINE
Hulkliikme tegurdamine tähendab hulkliikme ehk summa esitamist korrutisena.
- Ühise liikme sulgude ette toomine
Ühiseks teguriks võetakse üks liige, millega jaguvad kõik avaldise liikmed ja mis sisaldab kõiki võimalikke ühiseid tegureid.
Valem: ab + ac = a(b + c)
Näide: 2ab + 4a2c = 2a (b + 2ac)
- Korrutamise abivalemid:
Näited:
k2 – s2 = (k – s)(k + s)
Sulle võivad huvi pakkuda need õppematerjalid:
Ruutvõrrand
Liitmine 20 piires
Kell ja kellaaeg
Tasandilised kujundid
Ruutvõrrandi mõiste, ruutvõrrandi lahendivalem, ruutvõrrandi liigid
Funktsioonid ja nende graafikud
Numbrilised seosed
Ruutvõrrandi abil lahenduvad tekstülesanded
8. klassi matemaatika teooriavideod
Peastarvutamine eelkoolile
Kirjeldav statistika
II kooliastme matemaatika reeglite kordamine
Algebralised murrud
Funktsioonide graafikud
xy-koordinaatsüsteem
Allar Veelmaa videotund. Avaldised
Ruutjuur, tehted ruutjuurtega
Valik harjutusülesandeid matemaatika riigieksamiks
Liitmine 10 piires
Funktsioonide graafikute lõikepunktide leidmine
2us2 – 8uv2 = 2u(s2 – 4v2) = 2u(s – 4v)(s + 2v)
4 + 12c + 9c2 = (2 + 3c)2 = (2 + 3c)(2 + 3c)
2x3 + 8x2y + 8xy2 =2x(x2 + 4xy + 4y2) = 2x(x + 2y)2 = 2x(x + 2y)(x + 2y)
u2 – 2uv + v2 =(u – v)2 = (u –v)(u –v)
3x2y – 6xy +3y = 3y(x – 1)2 = 3y(x – 1)(x – 1)
Ruutkolmliikme tegurdamine
Ruutkolmliikme tegurdamist kasutan siis, kui kui on 3 liiget, aga korrutamise abivalemeid ei saa kasutada.
- Panen ruutkolmliikme võrduma nulliga.
- Lahendan ruutvõrrandi (leian x1 ja x2).
- Kirjutan ruutkolmliikme lahti tegurite korrutisena:
Taandatud ruutvõrrandi puhul:
x2 + px + q = (x – x1)(x – x2)
Taandamata ruutvõrrandi puhul:
ax2 + bx + c = a(x – x1)(x –x2)
Näide 1: x2 – 5x – 6
x2 – 5x – 6 = 0
x1 = –1ja x2 = 6
x2 – 5x – 6 = (x + 1)(x – 6)
Näide 2: 2x2 – 5x – 3
2x2 – 5x – 3 = 0
x1 = – 0,5 ja x2 = 3
2x2 – 5x – 3 = 2(x + 0,5)(x – 3) = (2x + 1)(x – 3)
Lisaks:
Märkasid viga? Anna sellest teada ja teeme TaskuTarga koos paremaks!