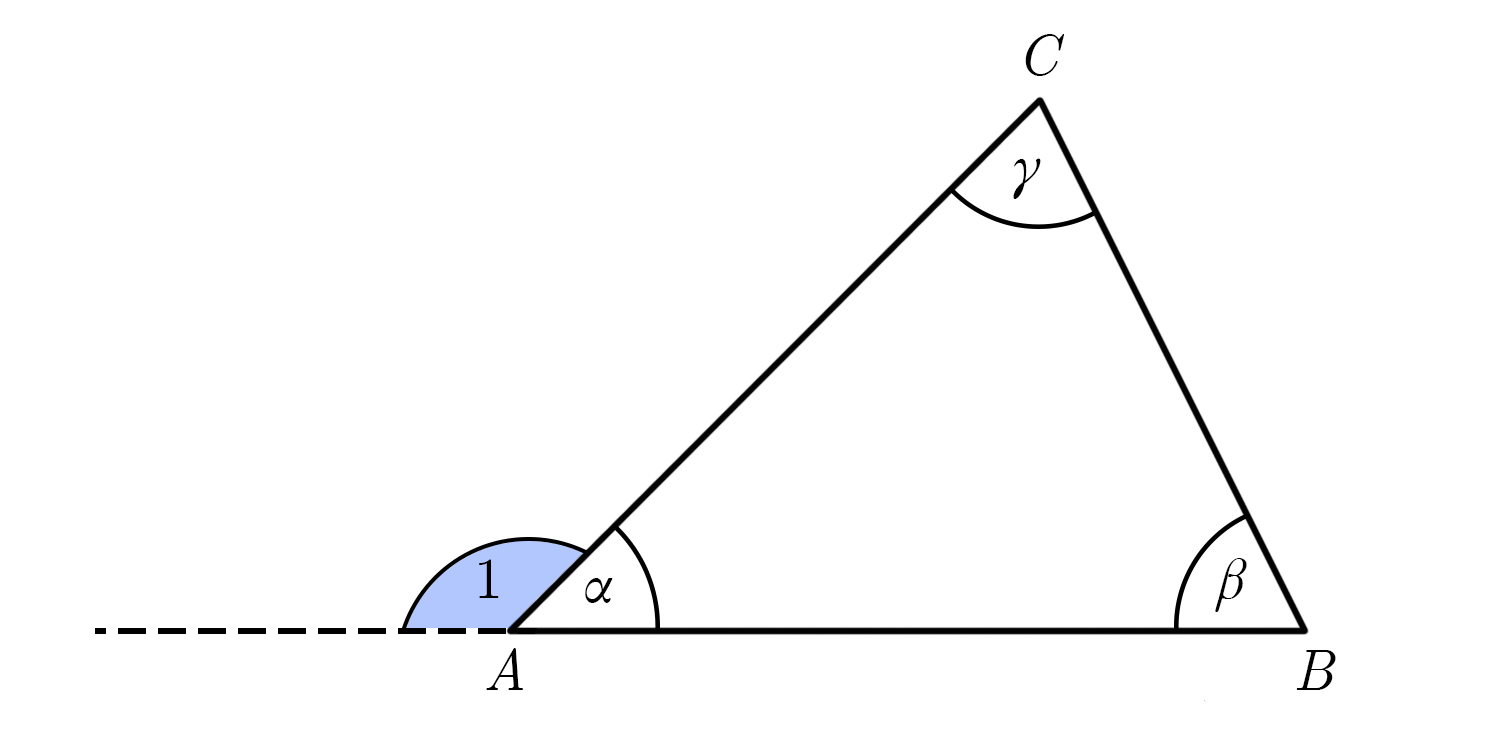
Kolmnurga nurga kõrvunurka nimetatakse kolmnurga välisnurgaks.
Nurk 1 on kolmnurga ABC nurga \(\alpha\) välisnurk. Nurk 1 ja nurk \(\alpha\) on kõrvunurgad. Kõrvunurkade summa on 180°. Seega, ∠1 + \(\alpha\) = 180°.
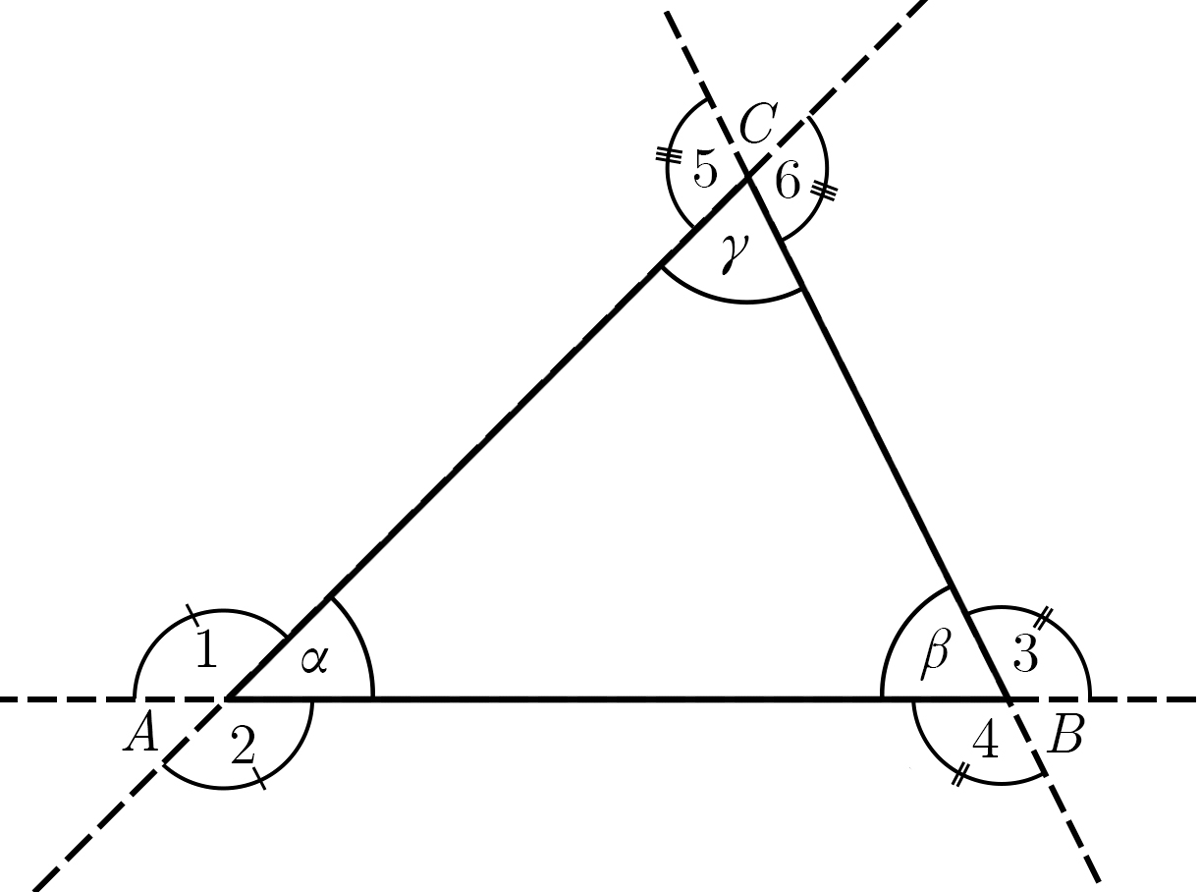
Igal kolmnurgal on kuus välisnurka.
Välisnurgad on paarikaupa võrdsed. Iga sisenurga välisnurgad on tippnurgad. Tippnurkade võrdsusest:
\[ ∠1= ∠2, \hspace{2mm} ∠3= ∠4 \hspace{2mm} \text{ ning }\hspace{2mm} ∠5= ∠6. \]
Kolmnurga välisnurkade summa on 360°:
\[ ∠1 + ∠3 + ∠5 = 360°. \]
Kolmnurga välisnurk võrdub temaga mitte kõrvuti olevate sisenurkade summaga.
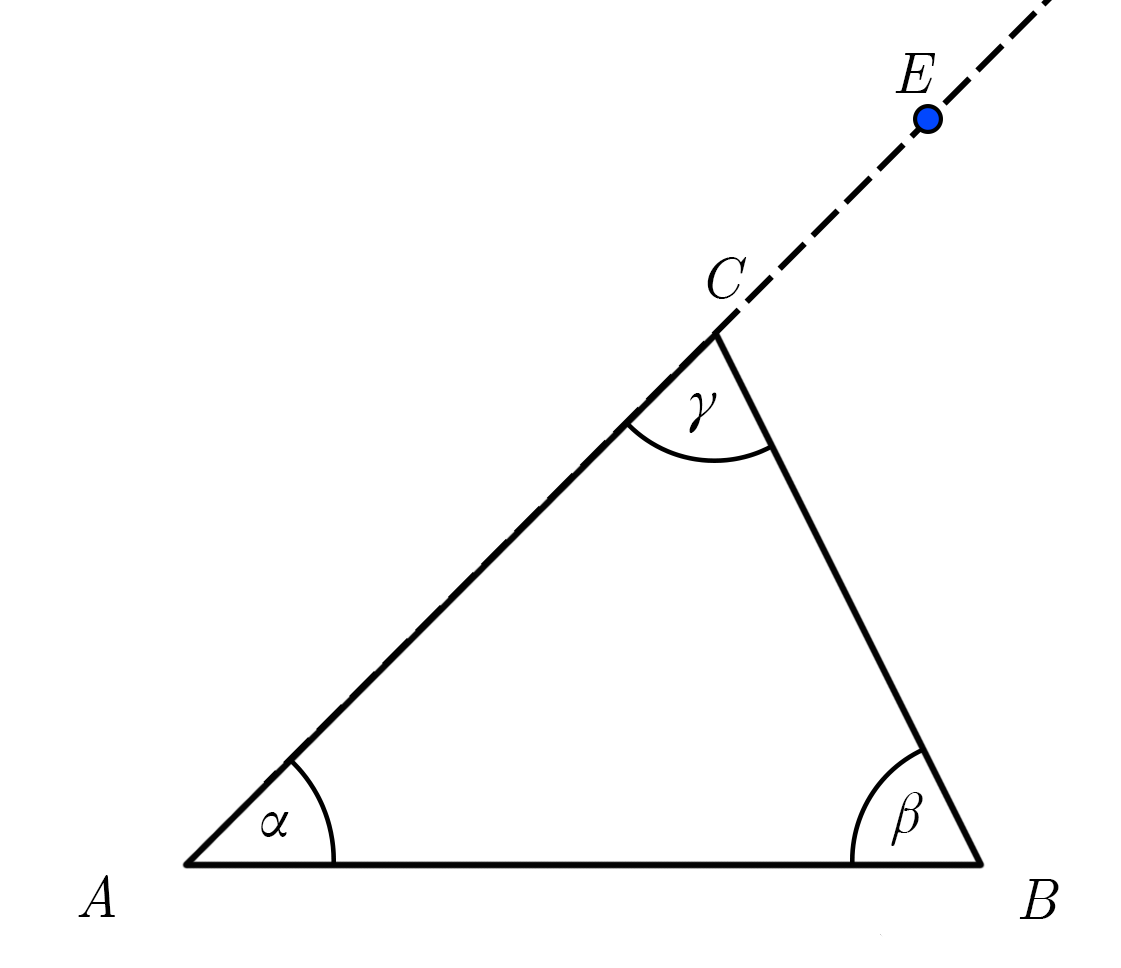
Vaatame kolmnurka ABC. Näitame, et \(∠ECB = \alpha + β. \)
Joonestame läbi kolmnurga ABC tipu C kolmnurga küljega AB paralleelse sirge s.
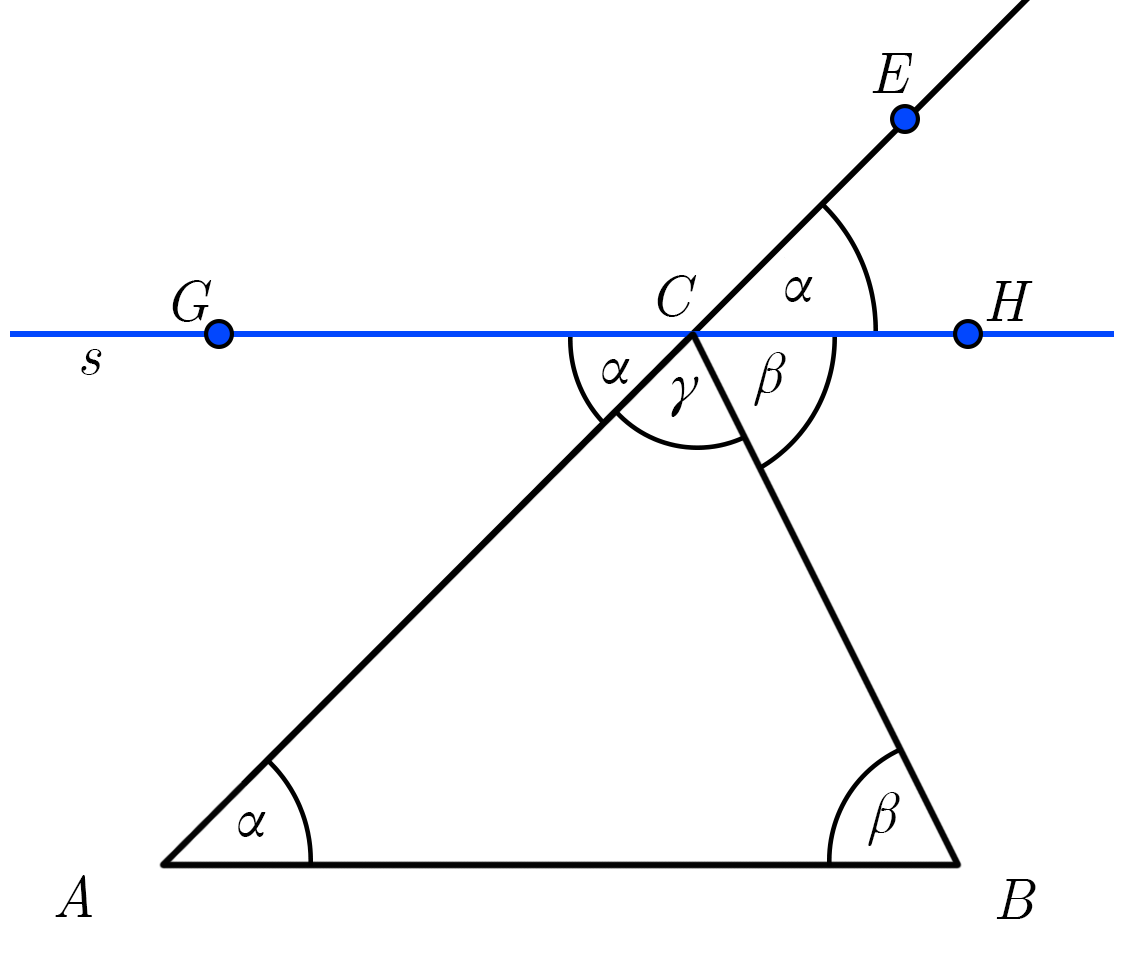
Kuna sirge s ja kolmnurga ABC külg AB on paralleelsed, siis kolmnurga nurk \(\alpha\) ja tekkinud nurk ∠GCA on võrdsed põiknurgad. Võrdsed on ka tippnurgad ∠GCA ja ∠HCE. Seega ∠GCA = ∠HCE = \(\alpha\).
Kuna sirge s ja kolmnurga ABC külg AB on paralleelsed, siis kolmnurga nurk β ja tekkinud nurk ∠HCB on võrdsed põiknurgad. Seega, ∠HCB = β.
Jooniselt näeme, et ∠ECB = \(\alpha\) + β.
Seega, nurga γ välisnurk ECB on võrdne nurkade \(\alpha\) ja β summaga.
M.O.T.T.
Lahendame näidisülesandeid kolmnurga välisnurkade kohta.
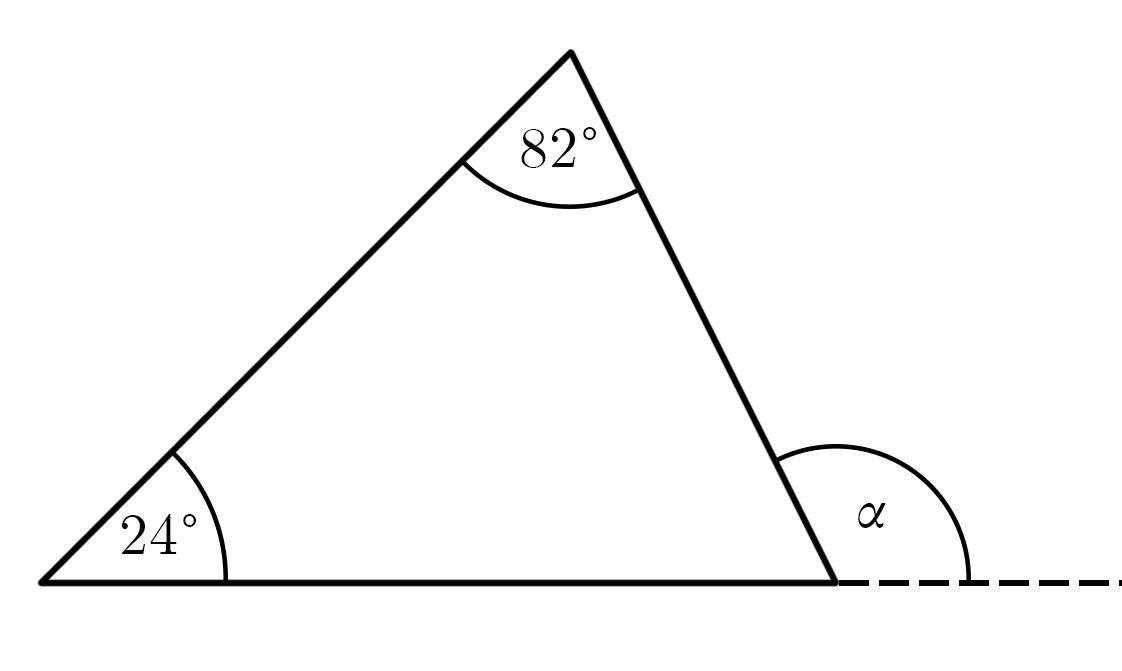
Ülesanne. Kolmnurga kahe nurga suurused on 24° ja 82°. Arvuta kolmnurga kolmanda nurga välisnurga suurus.
Lahendus.
Kolmnurga välisnurk võrdub temaga mitte kõrvuti olevate sisenurkade summaga. Seega,
\[\alpha = 24° + 82° = 106°.\]
Vastus.
Kolmanda nurga välisnurga suurus on 106°.
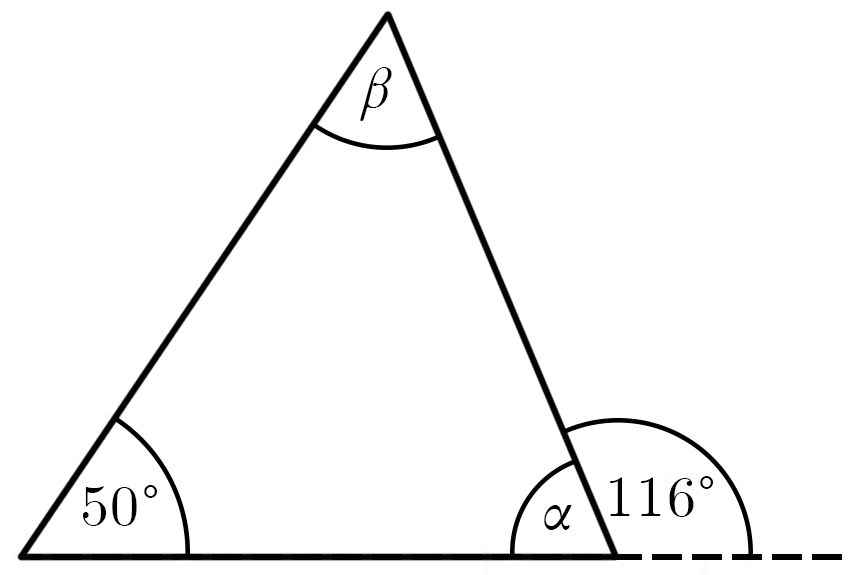
Ülesanne. Kolmnurga ühe välisnurga suurus on 116°. Temaga mitte kõrvuti oleva ühe sisenurga suurus on 50°. Arvuta kolmnurga kõigi sisenurkade suurused.
Lahendus.
Kolmnurga välisnurk võrdub temaga mitte kõrvuti olevate sisenurkade summaga. Seega,
\[ 50° + β = 116°,\]
millest nurga β suurus on
\[ β = 116° − 50° = 66°.\]
Kolmnurga nurk ja tema välisnurk on kõrvunurgad. Kõrvunurkade summa on 180°. Seega,
\[ \alpha + 116° = 180°,\]
millest
\[ \alpha = 180° − 116° = 64°.\]
Vastus.
Kolmnurga sisenurgad on 50°, 64° ja 66°.
Lahenda toodud näidete abil järgmised ülesanded kolmnurga välisnurkade kohta.
Ülesanded