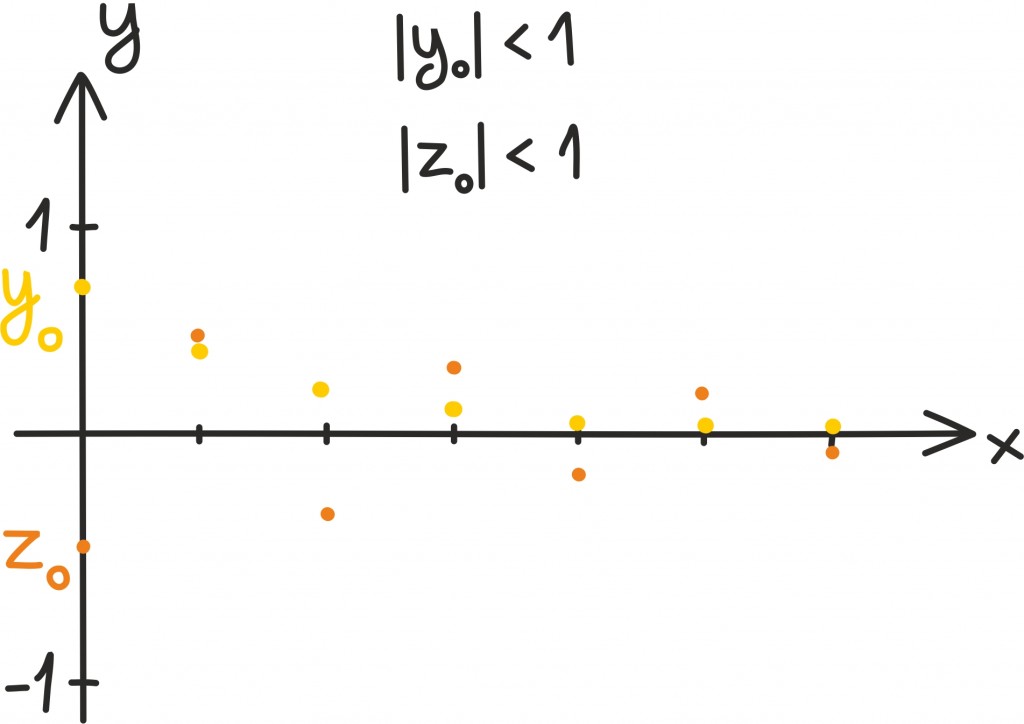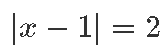Arvu absoluutväärtus

Joonistame arvtelje, lööme sinna naelaga keskele nulli, võtame nöörijupi ning tähistame kaks arvu a ja –a. Need arvud on nullpunktist samal kaugusel. Seda kaugust nullpunktist nimetatakse arvu absoluutväärtuseks.

Seega arvude 1 ja –1 absoluutväärtus on 1, kuna nad asuvad mõlemad nullpunktist täpselt ühiku kaugusel, ning samamoodi on arvude π ja –π mõlema absoluutväärtus π.

Sulle võivad huvi pakkuda need õppematerjalid:

Kuna arvu absoluutväärtus tähistab kaugust, ei saa ta muidugi olla negatiivne.

Arvu absoluutväärtust tähistatakse, asetades arv püstkriipsude vahele. Näiteks |1| = 1 ja |– 1| = 1. Võibki mõelda, et kriipsud suruvad miinuse kokku.

Matemaatiliselt võib arvu absoluutväärtuse defineerida nii:

kui x on positiivne, siis |x| = x,

kui x on negatiivne, siis |x| = –x,

kui x on võrdne nulliga, siis |0| = 0.

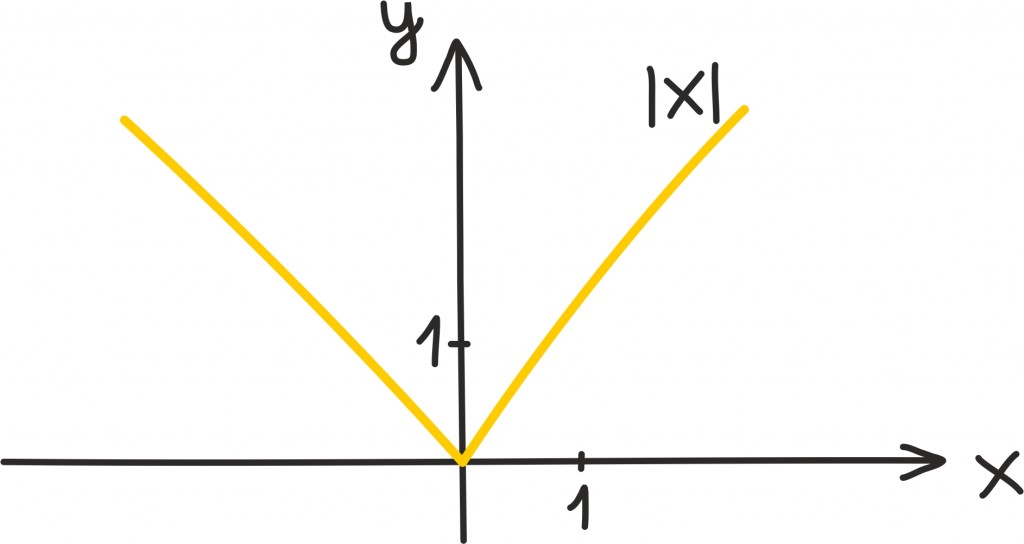
Kui leiame iga reaalarvu jaoks tema absoluutväärtuse, saame järgmise graafiku – funktsiooni |x| graafiku.

Oluline on võibolla ka märgata, et kuigi defineerisime arvu absoluutväärtuse kui tema kauguse nullist, võime absoluutväärtuse abil kirjeldada tõesti kõikide arvude vahelisi kauguseid. On ju arvude x ning yvahelise kauguse leidmine täpselt võrdne nende vahex – y (või miks ka mitte y – x) kaugusega nullpunktist.

Milleks meile arvu absoluutväärtus?

Selgub, et nii mõnigi kord oleneb arvude käitumine rohkem nende absoluutväärtusest kui nende täpsest asetusest arvteljel.

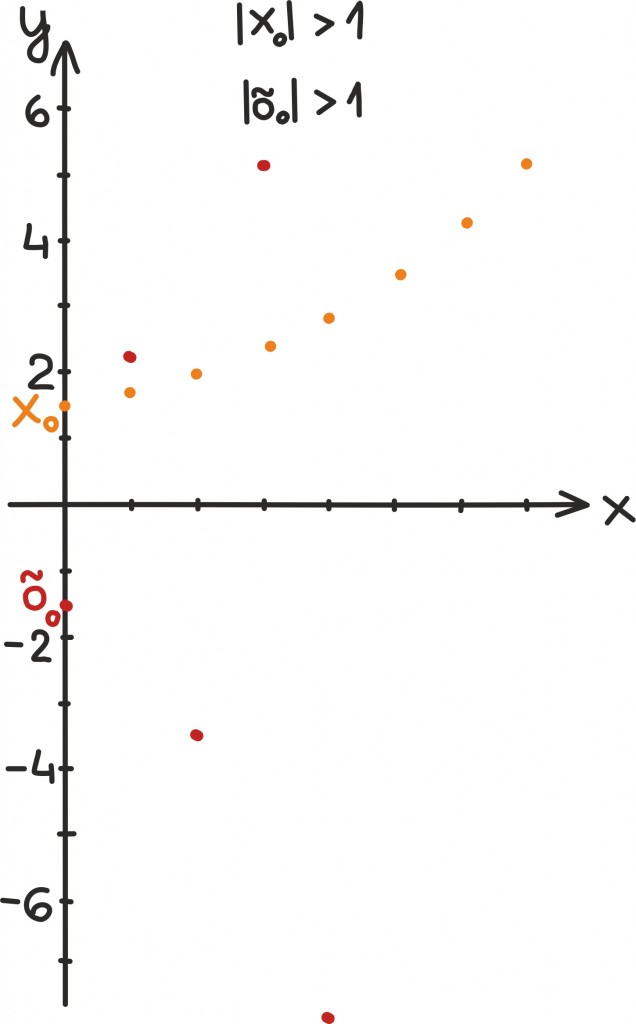
Oletame näiteks, et hakkame ühte arvu iseendaga korrutama. Kui selle arvu absoluutväärtus on suurem kui 1, satume nullist järjest kaugemale, kui aga arvu absoluutväärtus on 1-st väiksem, läheneme järjest nullile. Järgnevatel graafikutel oleme võtnud neli arvux₀, õ₀,y₀ ja z₀ ja hakanud neid iseendaga korrutama. Kahe esimese absoluutväärtus on ühest suurem ning nii suunduvad iseendaga korrutamisel saadud arvud nullist järjest kaugemale. Kahe viimase absoluutväärtus on ühest väiksem ning nende korrutised koonduvad nulli suunas.

Saadud arvude järjendeid kutsutakse geomeetriliseks jadaks ja nendega kohtume veel lähemalt [lk 131]!

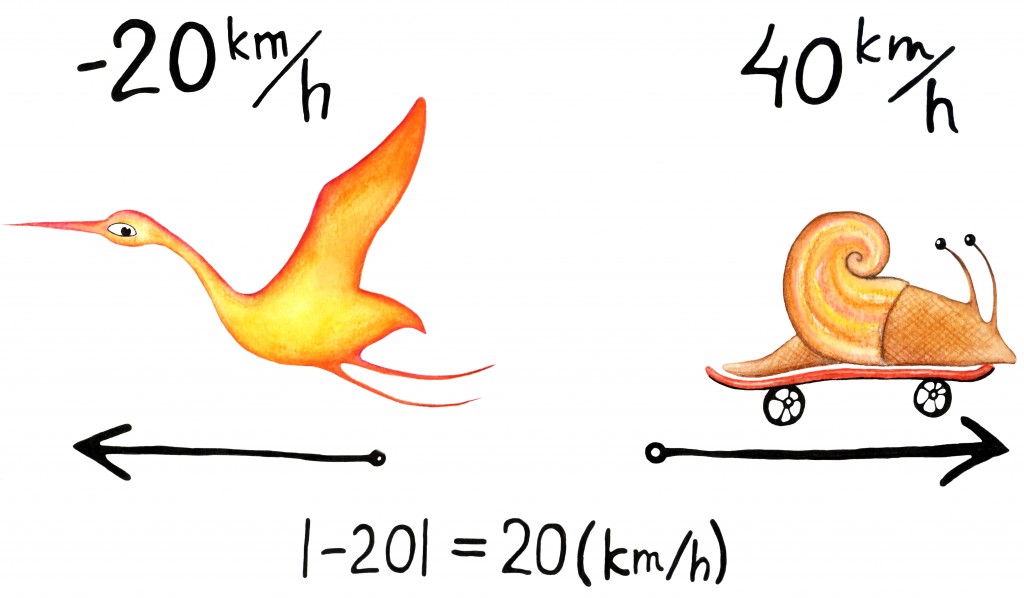
Arvu absoluutväärtus tuleb esile ka füüsikas, kus tihti huvitab meid mitte ühe või teise objekti positsioon, vaid hoopis objektide vaheline kaugus. Samamoodi võime mõelda ka kiirustest. Kui oleme ise näiteks keset pikka sirget teed ja lööme enda kõrvale nullpunkti, on meie poole liikuvatel objektidel negatiivne kiirus. Selle kiiruse suurust näitab siis tema absoluutväärtus.

Arvu absoluutväärtusega saab kirja panna ka võrrandeid [lk 168].

Näiteks võrrand kujus

tähendab, et otsitakse väärtusi x, mis on arvust 1 kaugusel 2. Absoluutväärtustega võrrandit käsitleme veidi pikemalt juba raamatu neljandas osas [lk 202].

Jada