Statistika on teadus, mis käsitleb andmete kogumist, töötlemist ja analüüsimist. Statistilised andmed on katse-, mõõtmis-, vaatlus-, küsitlus- jms. tulemused.

Andmete kogumine ja korrastamine on vajalik eeltöö statistilisele töötlemisele.

Andmete korrastamiseks reastame kõik andmed kasvavalt, mille tulemusel saame variatsioonrea.

Kanname need sagedustabelisse. Sagedustabel on tabel, mille ühes reas on tunnuse erinevad väärtused ja teises reas on nende väärtuste esinemise sagedus.

Lisaks sagedusele lisandub tabelisse uus lahter pealkirjaga „suhteline sagedus“.

Sagedus näitab, kui palju igat erinevat suurust andmete seas esineb. Suhteline sagedus näitab kui suure osa vastav suurus moodustab kõikidest andmetest. See leitakse suuruse esinemise sageduse jagamisel kogu andmete arvuga.

Sageli esitatakse suhteline sagedus protsentides. Selleks korrutatakse jagatis läbi 100%-ga. Kõigi suhteliste sageduste summa peab olema kokku 100%.

Kui andmed on korrastatud, siis järgneb sellele tihti parema ülevaate saamiseks joonise tegemine (joondiagramm, tulpdiagramm, sektordiagramm jne).

Keskväärtus, mood ja mediaan

Statistilise kogumi mõnedeks arvkarakteristikuteks on mood, mediaan ja keskmine.

Statistiliste andmete iseloomustamiseks leitakse ka nende andmete aritmeetiline keskmine.

Antud arvude aritmeetiliseks keskmiseks nimetatakse arvu, mis saadakse antud arvude summa jagamisel liidetavate arvuga. Tähistatakse sümboliga .

Keskmist arvutatakse:

a) variatsioonrea põhjal , kus  on tunnuse kõik väärtused ja n on näitab, mitu tunnuse väärtust on.

b) sagedustabeli põhjal , kus on tunnuse erinevad väärtused; f on antud tunnuse esinemise sagedus ja k on näitab, mitu tunnuse väärtust on.

Näide: Leia arvude 3, 4, 5 ja 6 aritmeetiline keskmine.

Aritmeetilise keskmise leidmiseks liidame antud arvud kokku ja jagame nende arvuga (arve on 4, jagame 4-ga):

Arvuta oma hinnete aritmeetiline keskmine (selleks sisesta oma hinded): http://www.matemaatika.edu.ee/sisu/0012/keskmine/index.html

Leia arvude aritmeetiline keskmine: http://www.thatquiz.org/tq-p-z0/?-j4g00-l4-p0

Mood (tähistatakse sümboliga Mo) on tunnuse kõige sagedamini esinev väärtus.

Moode võib olla rohkem kui üks.

Mediaan (tähistatakse sümboliga Me) on tunnuse väärtus, millest suuremaid ja väiksemaid väärtusi on võrdne arv.

Mediaani leitakse variatsioonrea abil. Kui väärtusi on paaritu arv, on mediaaniks täpselt keskmine arv variatsioonreast. Kui väärtusi on paarisarv, siis leiame mediaani nii, et liidame kaks keskmist arvu kokku ja jagame kahega.

Variatsiooni ulatus on tunnuse suurima ja vähima väärtuse vahe. See iseloomustab tunnuse väärtuse hajumist.

Lõpetuseks analüüsime saadud tulemusi ning teeme järeldusi.

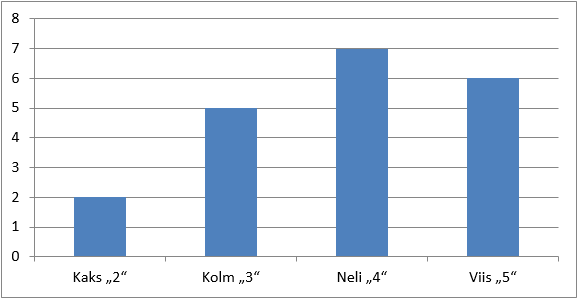
Näide: 9. klassi matemaatika kontrolltööde hinded olid 20 õpilasel järgmised:

3; 4; 4; 5; 2; 5; 4; 3; 5; 5; 4; 3; 3; 2; 4; 5; 3; 4; 4; 5

Korrasta andmed ja kanna need sagedustabelisse, leia ka hinnete suhteline sagedus.

Koostan variatsioonrea järjestades hinded kasvavalt:

2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 5

Teen järeldusi: Kõige rohkem saadi kontrolltöös hinnet „4“ 35% kõigist hinnetest. Järelikult on hinne 4 selle statistilise kogumi mood, st Mo = 4. Kõige vähem saadi hindeid „2“, 10% kõigist hinnetest. Viisi oli 30%. Võib öelda, et kontrolltöö oli sooritatud pigem hästi.

Mediaani leidmiseks uurin variatsioonrida. Mediaanist peab nii vasakule, kui ka paremale poole jääma võrdne arv väärtusi.

Antud kogumis on paarisarv väärtuseid, seega arvudest, millele tõmbasin kasti ümber, jääb nii vasakule, kui ka paremale võrdne arv tunnuseid. Leian mediaani:

Lisaks:

• Statistika ja tõenäosus 1
• Statistika ja tõenäosus 2